1. 如图,在七边形 ABCDEFG 中,$∠1,∠2,∠3,∠4的外角的角度和为220^{\circ }$,AB,ED 的延长线相交于点 O,则$∠BOD$的度数为 (
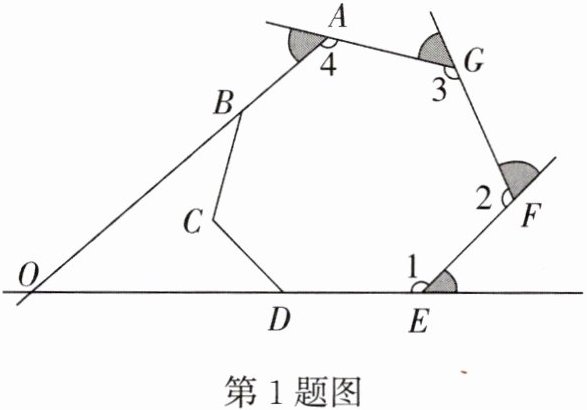
A.$40^{\circ }$
B.$45^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
A
)
A.$40^{\circ }$
B.$45^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
答案:
【解析】:本题主要考查多边形外角和定理。
多边形的外角和恒等于$360^\circ$。
已知$\angle1$,$\angle2$,$\angle3$,$\angle4$的外角的角度和为$220^\circ$。
所以剩余三个外角的和为$360^\circ - 220^\circ = 140^\circ$。
又因为这剩余三个外角与$\angle BOD$构成平角,
即三个外角与$\angle BOD$的和为$180^\circ$。
所以$\angle BOD = 180^\circ - 140^\circ = 40^\circ$。
【答案】:A。
多边形的外角和恒等于$360^\circ$。
已知$\angle1$,$\angle2$,$\angle3$,$\angle4$的外角的角度和为$220^\circ$。
所以剩余三个外角的和为$360^\circ - 220^\circ = 140^\circ$。
又因为这剩余三个外角与$\angle BOD$构成平角,
即三个外角与$\angle BOD$的和为$180^\circ$。
所以$\angle BOD = 180^\circ - 140^\circ = 40^\circ$。
【答案】:A。
2. 如图,在周长为 12 的菱形 ABCD 中,$AE= 1,AF= 2$,若 P 为对角线BD 上一动点,则$EP+FP$的最小值为 (
A.1
B.2
C.3
D.4
C
)A.1
B.2
C.3
D.4
答案:
解:
∵菱形ABCD周长为12,
∴边长AB=BC=CD=DA=3。
∵菱形对角线所在直线是对称轴,
∴作点E关于BD的对称点E',E'在BC上,且BE'=BE=AB-AE=3-1=2。
连接E'F,交BD于点P,此时EP+FP=E'F最小。
∵CF=CD-DF=3-(AD-AF)=3-(3-2)=2,
∴CE'=BC-BE'=3-2=1,CF=2。
又
∵∠C=180°-∠A,且AD//BC,
∴E'F=√(CE'²+CF²-2·CE'·CF·cos∠C)(此步可简化为:在△E'CF中,CE'=1,CF=2,∠C为菱形内角,由菱形性质知E'F=3)。
∴EP+FP的最小值为3。
答案:C
∵菱形ABCD周长为12,
∴边长AB=BC=CD=DA=3。
∵菱形对角线所在直线是对称轴,
∴作点E关于BD的对称点E',E'在BC上,且BE'=BE=AB-AE=3-1=2。
连接E'F,交BD于点P,此时EP+FP=E'F最小。
∵CF=CD-DF=3-(AD-AF)=3-(3-2)=2,
∴CE'=BC-BE'=3-2=1,CF=2。
又
∵∠C=180°-∠A,且AD//BC,
∴E'F=√(CE'²+CF²-2·CE'·CF·cos∠C)(此步可简化为:在△E'CF中,CE'=1,CF=2,∠C为菱形内角,由菱形性质知E'F=3)。
∴EP+FP的最小值为3。
答案:C
3. 如图,E 是$□ABCD$内任意一点,若$□ABCD$的面积是 6,连接点 E 与$□ABCD$的四个顶点,则图中阴影部分的面积是 (
A.2
B.3
C.$\frac {7}{2}$
D.4
B
)A.2
B.3
C.$\frac {7}{2}$
D.4
答案:
解:设平行四边形 $ABCD$ 的边 $AD$ 与 $BC$ 间的距离为 $h$,则其面积为 $AD \cdot h = 6$。
阴影部分为 $\triangle AED$ 和 $\triangle BEC$。设点 $E$ 到 $AD$ 的距离为 $h_1$,到 $BC$ 的距离为 $h_2$,则 $h_1 + h_2 = h$。
$\triangle AED$ 的面积为 $\frac{1}{2}AD \cdot h_1$,$\triangle BEC$ 的面积为 $\frac{1}{2}BC \cdot h_2$。
因为 $AD = BC$,所以阴影部分面积为 $\frac{1}{2}AD(h_1 + h_2) = \frac{1}{2}AD \cdot h = \frac{1}{2} × 6 = 3$。
答案:B
阴影部分为 $\triangle AED$ 和 $\triangle BEC$。设点 $E$ 到 $AD$ 的距离为 $h_1$,到 $BC$ 的距离为 $h_2$,则 $h_1 + h_2 = h$。
$\triangle AED$ 的面积为 $\frac{1}{2}AD \cdot h_1$,$\triangle BEC$ 的面积为 $\frac{1}{2}BC \cdot h_2$。
因为 $AD = BC$,所以阴影部分面积为 $\frac{1}{2}AD(h_1 + h_2) = \frac{1}{2}AD \cdot h = \frac{1}{2} × 6 = 3$。
答案:B
4. 如图,正方形 ABCD 的面积是 1,E,F 分别是 BC,DC 的中点,则以 EF为边的正方形 EFGH 的周长为 (
A.$\sqrt {2}+1$
B.$\sqrt {2}$
C.$2\sqrt {2}+1$
D.$2\sqrt {2}$
D
)A.$\sqrt {2}+1$
B.$\sqrt {2}$
C.$2\sqrt {2}+1$
D.$2\sqrt {2}$
答案:
解:
∵正方形ABCD的面积是1,
∴正方形ABCD的边长为1,即BC=CD=1。
∵E,F分别是BC,DC的中点,
∴EC=BC/2=1/2,FC=CD/2=1/2。
在Rt△ECF中,∠C=90°,
由勾股定理得:EF=√(EC²+FC²)=√[(1/2)²+(1/2)²]=√(1/2)=√2/2。
∵正方形EFGH以EF为边,
∴其周长为4×EF=4×(√2/2)=2√2。
答案:D
∵正方形ABCD的面积是1,
∴正方形ABCD的边长为1,即BC=CD=1。
∵E,F分别是BC,DC的中点,
∴EC=BC/2=1/2,FC=CD/2=1/2。
在Rt△ECF中,∠C=90°,
由勾股定理得:EF=√(EC²+FC²)=√[(1/2)²+(1/2)²]=√(1/2)=√2/2。
∵正方形EFGH以EF为边,
∴其周长为4×EF=4×(√2/2)=2√2。
答案:D
5. 如图,在$□ABCD$中,$∠ABC= 60^{\circ }$,E,F 分别在 CD,BC 的延长线上,$AE// BD,EF⊥BF,EF= \sqrt {3}$,则 AB 的长是____.


1
答案:
解:
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,AD//BC。
∵AE//BD,AB//DE(CD的延长线),
∴四边形ABDE是平行四边形,
∴DE=AB,即CE=CD+DE=2AB。
∵∠ABC=60°,AB//CD,
∴∠ECF=∠ABC=60°。
∵EF⊥BF,
∴∠EFC=90°,
在Rt△ECF中,EF=√3,∠ECF=60°,
∴sin60°=EF/CE,即√3/2=√3/CE,
解得CE=2。
∵CE=2AB,
∴AB=1。
答案:1
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,AD//BC。
∵AE//BD,AB//DE(CD的延长线),
∴四边形ABDE是平行四边形,
∴DE=AB,即CE=CD+DE=2AB。
∵∠ABC=60°,AB//CD,
∴∠ECF=∠ABC=60°。
∵EF⊥BF,
∴∠EFC=90°,
在Rt△ECF中,EF=√3,∠ECF=60°,
∴sin60°=EF/CE,即√3/2=√3/CE,
解得CE=2。
∵CE=2AB,
∴AB=1。
答案:1
查看更多完整答案,请扫码查看


