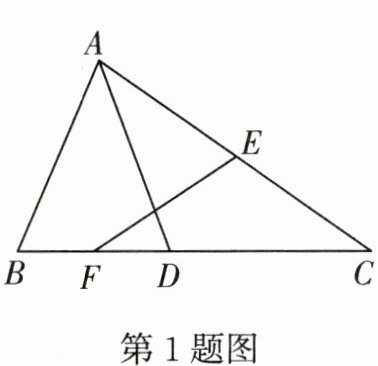
1.如图,在△ABC中,D是BC边上一点,AB= AD,E,F分别是AC,BD的中点,EF= 2,则AC的长是 (
A.3
B.4
C.5
D.6
B
)
A.3
B.4
C.5
D.6
答案:
【解析】:本题可根据等腰三角形三线合一的性质以及三角形中位线定理来求解$AC$的长。
步骤一:连接$AF$
因为$AB = AD$,$F$是$BD$的中点,根据等腰三角形三线合一的性质(等腰三角形底边上的高、底边上的中线、顶角平分线相互重合),可知$AF\perp BD$,即$\angle AFD = 90^{\circ}$。
步骤二:利用三角形中位线定理
由于$E$是$AC$的中点,在$Rt\triangle AFC$中,根据直角三角形斜边中线定理(直角三角形斜边的中线等于斜边的一半),可得$EF=\frac{1}{2}AC$。
步骤三:计算$AC$的长
已知$EF = 2$,由$EF=\frac{1}{2}AC$,可得$AC = 2EF = 2×2 = 4$。
【答案】:B
步骤一:连接$AF$
因为$AB = AD$,$F$是$BD$的中点,根据等腰三角形三线合一的性质(等腰三角形底边上的高、底边上的中线、顶角平分线相互重合),可知$AF\perp BD$,即$\angle AFD = 90^{\circ}$。
步骤二:利用三角形中位线定理
由于$E$是$AC$的中点,在$Rt\triangle AFC$中,根据直角三角形斜边中线定理(直角三角形斜边的中线等于斜边的一半),可得$EF=\frac{1}{2}AC$。
步骤三:计算$AC$的长
已知$EF = 2$,由$EF=\frac{1}{2}AC$,可得$AC = 2EF = 2×2 = 4$。
【答案】:B
2.如图,将三边分别为3,4,5的△ABC,沿最长边AB翻折180°成$△ABC_1,$则$CC_1$的长为 (
A.$\frac{12}{5}$
B.$\frac{5}{12}$
C.$\frac{5}{6}$
D.$\frac{24}{5}$
D
)A.$\frac{12}{5}$
B.$\frac{5}{12}$
C.$\frac{5}{6}$
D.$\frac{24}{5}$
答案:
【解析】:本题主要考察勾股定理的逆定理和折叠的性质。
首先,根据勾股定理的逆定理,若三角形三边满足$a^2 + b^2 = c^2$,则该三角形是直角三角形。
对于$\bigtriangleup ABC$,三边分别为3,4,5,满足$3^2 + 4^2 = 5^2$,所以$\bigtriangleup ABC$是直角三角形,且$\angle C = 90^\circ$。
当$\bigtriangleup ABC$沿最长边$AB$翻折$180^\circ$成$\bigtriangleup ABC_1$时,$CC_1$垂直于$AB$,且$C$和$C_1$关于$AB$对称。
设$AB$与$CC_1$相交于点$D$,则$CD = C_1D$,且$CD \perp AB$。
利用直角三角形的面积公式,有$\frac{1}{2} × AC × BC = \frac{1}{2} × AB × CD$。
代入已知数值,得:
$\frac{1}{2} × 3 × 4 = \frac{1}{2} × 5 × CD$,
解得$CD = \frac{12}{5}$。
由于$C$和$C_1$关于$AB$对称,所以$CC_1 = 2 × CD = 2 × \frac{12}{5} = \frac{24}{5}$。
【答案】:D. $\frac{24}{5}$。
首先,根据勾股定理的逆定理,若三角形三边满足$a^2 + b^2 = c^2$,则该三角形是直角三角形。
对于$\bigtriangleup ABC$,三边分别为3,4,5,满足$3^2 + 4^2 = 5^2$,所以$\bigtriangleup ABC$是直角三角形,且$\angle C = 90^\circ$。
当$\bigtriangleup ABC$沿最长边$AB$翻折$180^\circ$成$\bigtriangleup ABC_1$时,$CC_1$垂直于$AB$,且$C$和$C_1$关于$AB$对称。
设$AB$与$CC_1$相交于点$D$,则$CD = C_1D$,且$CD \perp AB$。
利用直角三角形的面积公式,有$\frac{1}{2} × AC × BC = \frac{1}{2} × AB × CD$。
代入已知数值,得:
$\frac{1}{2} × 3 × 4 = \frac{1}{2} × 5 × CD$,
解得$CD = \frac{12}{5}$。
由于$C$和$C_1$关于$AB$对称,所以$CC_1 = 2 × CD = 2 × \frac{12}{5} = \frac{24}{5}$。
【答案】:D. $\frac{24}{5}$。
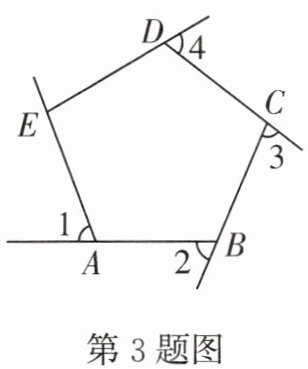
3.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1= ∠2= ∠3= ∠4= 70°,则∠AED的度数是 (
A.80°
B.100°
C.108°
D.110°
B
)
A.80°
B.100°
C.108°
D.110°
答案:
【解析】:
本题考查的知识点是多边形外角和定理。
多边形的外角和定理:任意多边形的外角和都为$360^\circ$。
题目给出五边形ABCDE的四个外角∠1, ∠2, ∠3, ∠4的度数都是$70^\circ$。
根据外角和定理,五边形的所有外角和为$360^\circ$。
由此可以计算出第五个外角∠5的度数:
$\angle 5 = 360^\circ - (\angle 1 + \angle 2 + \angle 3 + \angle 4) = 360^\circ - (70^\circ × 4) = 360^\circ - 280^\circ = 80^\circ$。
由于外角与相邻内角互补,即它们的度数和为$180^\circ$,
因此,$\angle AED = 180^\circ - \angle 5 = 180^\circ - 80^\circ = 100^\circ$。
【答案】:B
本题考查的知识点是多边形外角和定理。
多边形的外角和定理:任意多边形的外角和都为$360^\circ$。
题目给出五边形ABCDE的四个外角∠1, ∠2, ∠3, ∠4的度数都是$70^\circ$。
根据外角和定理,五边形的所有外角和为$360^\circ$。
由此可以计算出第五个外角∠5的度数:
$\angle 5 = 360^\circ - (\angle 1 + \angle 2 + \angle 3 + \angle 4) = 360^\circ - (70^\circ × 4) = 360^\circ - 280^\circ = 80^\circ$。
由于外角与相邻内角互补,即它们的度数和为$180^\circ$,
因此,$\angle AED = 180^\circ - \angle 5 = 180^\circ - 80^\circ = 100^\circ$。
【答案】:B
4.点A,B,C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A,B,C,D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有 (
A.1个
B.2个
C.3个
D.4个
C
)A.1个
B.2个
C.3个
D.4个
答案:
【解析】:
本题主要考查平行四边形的性质,即平行四边形的对角线互相平分。
题目中给出了三个不共线的点A、B、C,需要找到一个点D,使得这四个点能构成一个平行四边形。
我们可以按照以下步骤来寻找点D:
假设以AB和BC为邻边作平行四边形,那么根据平行四边形的性质,点D应当位于以BC为对角线的平移位置上,即存在一个点D1,使得AD1与BC平行且等长,同时BD1与AC平行且等长。
同理,若以AB和AC为邻边作平行四边形,会存在一个点D2满足条件。
若以AC和BC为邻边作平行四边形,会存在一个点D3满足条件。
因此,平面上符合这样条件的点D有3个。
【答案】:
C. 3个。
本题主要考查平行四边形的性质,即平行四边形的对角线互相平分。
题目中给出了三个不共线的点A、B、C,需要找到一个点D,使得这四个点能构成一个平行四边形。
我们可以按照以下步骤来寻找点D:
假设以AB和BC为邻边作平行四边形,那么根据平行四边形的性质,点D应当位于以BC为对角线的平移位置上,即存在一个点D1,使得AD1与BC平行且等长,同时BD1与AC平行且等长。
同理,若以AB和AC为邻边作平行四边形,会存在一个点D2满足条件。
若以AC和BC为邻边作平行四边形,会存在一个点D3满足条件。
因此,平面上符合这样条件的点D有3个。
【答案】:
C. 3个。
查看更多完整答案,请扫码查看


