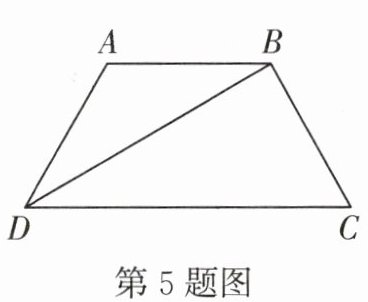
5.如图,已知$AB// CD,AD= AB= BC,DC= 2AB$,则$∠DBC$的度数为____.

$30^\circ$
答案:
【解析】:本题考查了平行四边形的判定与性质,等腰三角形的性质,等边三角形的判定与性质,利用等腰三角形的性质,平行四边形的性质,等边三角形的判定与性质解决问题是解题的关键。
由题可知$AB// CD$,$AB=AD=BC$,$DC=2AB$,
可设想取$DC$的中点$E$,连接$BE$、$BD$,
从而可得出四边形$ABED$为平行四边形和$△BEC$为等腰三角形,
进而可得出$BE=AB=EC$,
所以$△BEC$为等边三角形,
从而得到$\angle C=60^\circ$,
又因为$AD=AB=BC$,
可得出$\angle ADB=\angle ABD$,$\angle C=\angle CDB=\angle CBD=60^\circ$,
再利用三角形的内角和是$180^\circ$,
即可求出$\angle DBC$的度数。
解:取$DC$的中点$E$,连接$BE$、$BD$,
$\because AB// CD$,$AB=AD=BC$,$DC=2AB$,
$\therefore AB=DE=EC$,$AB// DE$,
$\because$一组对边平行且相等的四边形是平行四边形,
$\therefore$四边形$ABED$为平行四边形,
$\therefore AD=BE$,$AD// BE$,
$\because AD=BC$,
$\therefore BE=BC$,
$\because EC=BE=BC$,
$\therefore \triangle BEC$为等边三角形,
$\therefore \angle C=60^\circ$,
$\because AD=AB$,
$\therefore \angle ADB=\angle ABD$,
$\because BC=AD$,
$\therefore BC=BD$,
$\therefore \angle C=\angle CDB=\angle CBD=60^\circ$,
$\because \angle C+\angle CDB+\angle CBD=180^\circ$,
$\therefore \angle DBC=180^\circ-\angle C-\angle CDB=180^\circ-60^\circ-60^\circ=60^\circ$,
$\because \angle ABC=180^\circ-\angle C=180^\circ-60^\circ=120^\circ$,
$\therefore \angle DBA=\angle ABC-\angle DBC=120^\circ-60^\circ=60^\circ-\angle ADB$,
$\because \angle DBA+\angle ADB+\angle BAD=180^\circ$,
$\therefore \angle BAD=180^\circ-\angle DBA-\angle ADB=180^\circ-60^\circ=30^\circ$,
$\therefore \angle DBC=30^\circ$。
【答案】:$30^\circ$。
由题可知$AB// CD$,$AB=AD=BC$,$DC=2AB$,
可设想取$DC$的中点$E$,连接$BE$、$BD$,
从而可得出四边形$ABED$为平行四边形和$△BEC$为等腰三角形,
进而可得出$BE=AB=EC$,
所以$△BEC$为等边三角形,
从而得到$\angle C=60^\circ$,
又因为$AD=AB=BC$,
可得出$\angle ADB=\angle ABD$,$\angle C=\angle CDB=\angle CBD=60^\circ$,
再利用三角形的内角和是$180^\circ$,
即可求出$\angle DBC$的度数。
解:取$DC$的中点$E$,连接$BE$、$BD$,
$\because AB// CD$,$AB=AD=BC$,$DC=2AB$,
$\therefore AB=DE=EC$,$AB// DE$,
$\because$一组对边平行且相等的四边形是平行四边形,
$\therefore$四边形$ABED$为平行四边形,
$\therefore AD=BE$,$AD// BE$,
$\because AD=BC$,
$\therefore BE=BC$,
$\because EC=BE=BC$,
$\therefore \triangle BEC$为等边三角形,
$\therefore \angle C=60^\circ$,
$\because AD=AB$,
$\therefore \angle ADB=\angle ABD$,
$\because BC=AD$,
$\therefore BC=BD$,
$\therefore \angle C=\angle CDB=\angle CBD=60^\circ$,
$\because \angle C+\angle CDB+\angle CBD=180^\circ$,
$\therefore \angle DBC=180^\circ-\angle C-\angle CDB=180^\circ-60^\circ-60^\circ=60^\circ$,
$\because \angle ABC=180^\circ-\angle C=180^\circ-60^\circ=120^\circ$,
$\therefore \angle DBA=\angle ABC-\angle DBC=120^\circ-60^\circ=60^\circ-\angle ADB$,
$\because \angle DBA+\angle ADB+\angle BAD=180^\circ$,
$\therefore \angle BAD=180^\circ-\angle DBA-\angle ADB=180^\circ-60^\circ=30^\circ$,
$\therefore \angle DBC=30^\circ$。
【答案】:$30^\circ$。
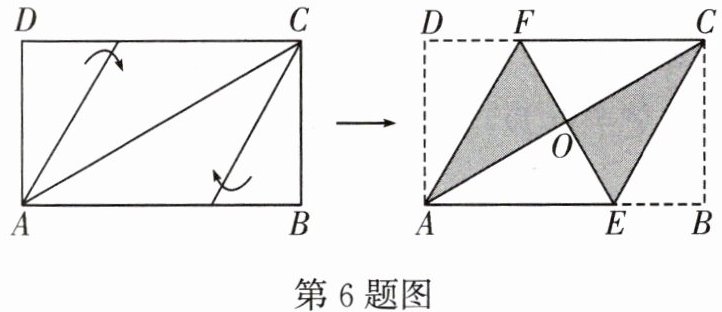
6.将矩形纸片ABCD按如图所示方式折叠,恰好得到菱形AECF.若$AB= 3$,则菱形AECF的周长为____.

8
答案:
解:设菱形AECF的边长为$x$。
因为四边形AECF是菱形,所以$AE = CE = x$。
由于矩形纸片ABCD折叠后得到菱形AECF,所以$BE = AB - AE = 3 - x$,且$\angle B = 90^\circ$。
在$Rt\triangle BCE$中,$BC^2 + BE^2 = CE^2$。
又因为菱形对角线互相垂直平分,设$AC$与$EF$交于点$O$,则$AO = OC$,$EO = OF$,且$AC \perp EF$。
由折叠性质知$AD = BC$,$AD = AF$,而$AF = AE = x$,在矩形中$AD = BC$,设$BC = y$,则$y^2 + (3 - x)^2 = x^2$。
又因为$AC$是矩形对角线,$AC = 2AO$,在$Rt\triangle ABC$中,$AC^2 = AB^2 + BC^2 = 9 + y^2$。
在菱形中,$AO = \frac{AC}{2}$,$EO = \frac{EF}{2}$,且$AO^2 + EO^2 = AE^2$,但$EO = BE = 3 - x$(折叠对应关系),所以$(\frac{AC}{2})^2 + (3 - x)^2 = x^2$。
而$AC^2 = 9 + y^2$,且$y^2 = x^2 - (3 - x)^2$,代入可得$AC^2 = 9 + x^2 - (3 - x)^2 = 6x$,则$(\frac{\sqrt{6x}}{2})^2 + (3 - x)^2 = x^2$,化简得$\frac{6x}{4} + 9 - 6x + x^2 = x^2$,即$\frac{3x}{2} + 9 - 6x = 0$,解得$x = 2$。
菱形周长为$4x = 4×2 = 8$。
答案:8
因为四边形AECF是菱形,所以$AE = CE = x$。
由于矩形纸片ABCD折叠后得到菱形AECF,所以$BE = AB - AE = 3 - x$,且$\angle B = 90^\circ$。
在$Rt\triangle BCE$中,$BC^2 + BE^2 = CE^2$。
又因为菱形对角线互相垂直平分,设$AC$与$EF$交于点$O$,则$AO = OC$,$EO = OF$,且$AC \perp EF$。
由折叠性质知$AD = BC$,$AD = AF$,而$AF = AE = x$,在矩形中$AD = BC$,设$BC = y$,则$y^2 + (3 - x)^2 = x^2$。
又因为$AC$是矩形对角线,$AC = 2AO$,在$Rt\triangle ABC$中,$AC^2 = AB^2 + BC^2 = 9 + y^2$。
在菱形中,$AO = \frac{AC}{2}$,$EO = \frac{EF}{2}$,且$AO^2 + EO^2 = AE^2$,但$EO = BE = 3 - x$(折叠对应关系),所以$(\frac{AC}{2})^2 + (3 - x)^2 = x^2$。
而$AC^2 = 9 + y^2$,且$y^2 = x^2 - (3 - x)^2$,代入可得$AC^2 = 9 + x^2 - (3 - x)^2 = 6x$,则$(\frac{\sqrt{6x}}{2})^2 + (3 - x)^2 = x^2$,化简得$\frac{6x}{4} + 9 - 6x + x^2 = x^2$,即$\frac{3x}{2} + 9 - 6x = 0$,解得$x = 2$。
菱形周长为$4x = 4×2 = 8$。
答案:8
7.如图,将$□ ABCD$的边AB延长至点E,使$BE= AB$,连接DE,EC,BD,DE交BC于点O.
(1)求证:$△ABD\cong △BEC$.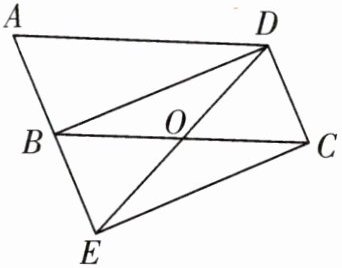
(2)若$∠BOD= 2∠A$,求证:四边形BECD是矩形.
(1)求证:$△ABD\cong △BEC$.

(2)若$∠BOD= 2∠A$,求证:四边形BECD是矩形.
答案:
(1)证明:
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AB//CD,∠A=∠BCD,
∵BE=AB,
∴BE=CD,
∵AB//CD,
∴BE//CD,
∴四边形BECD是平行四边形,
∴BD=EC,
在△ABD和△BEC中,
$\left\{\begin{array}{l}AB=BE\\ AD=BC\\ BD=EC\end{array}\right.$,
∴△ABD≌△BEC(SSS);
(2)证明:
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,AD//BC,
∴∠A+∠ABC=180°,
∵∠BOD=2∠A,∠BOD=∠OBC+∠ODC,
∵四边形BECD是平行四边形,
∴OD=OE,OC=OB,BE//CD,
∴∠OBC=∠BCD=∠A,
∴∠ODC=∠BOD-∠OBC=2∠A-∠A=∠A,
∴∠ODC=∠BCD,
∴OC=OD,
∴2OC=2OD,即BC=DE,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形。
(1)证明:
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AB//CD,∠A=∠BCD,
∵BE=AB,
∴BE=CD,
∵AB//CD,
∴BE//CD,
∴四边形BECD是平行四边形,
∴BD=EC,
在△ABD和△BEC中,
$\left\{\begin{array}{l}AB=BE\\ AD=BC\\ BD=EC\end{array}\right.$,
∴△ABD≌△BEC(SSS);
(2)证明:
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,AD//BC,
∴∠A+∠ABC=180°,
∵∠BOD=2∠A,∠BOD=∠OBC+∠ODC,
∵四边形BECD是平行四边形,
∴OD=OE,OC=OB,BE//CD,
∴∠OBC=∠BCD=∠A,
∴∠ODC=∠BOD-∠OBC=2∠A-∠A=∠A,
∴∠ODC=∠BCD,
∴OC=OD,
∴2OC=2OD,即BC=DE,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形。
某数学兴趣小组在进行探究活动时提出了如下问题:如图1,在$△ABC$中,若$AB= 5,AC= 3$,那么BC边上的中线AD的取值在什么范围内呢?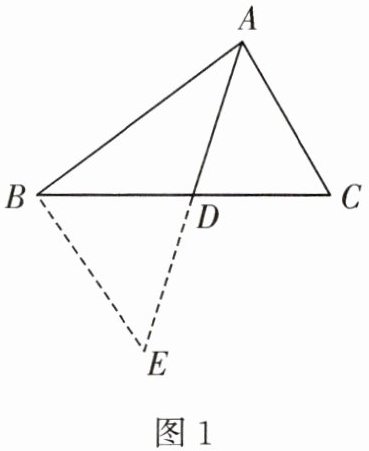
解决方法:延长AD到E,使得$DE= AD$,再连接BE,可得$BE= AC$.把AB,AC,2AD集中在$△ABE$中,利用三角形的三边关系可得$2<AE<8$,则$1<AD<4$.
迁移应用:请参考上述解题方法,证明下列命题.
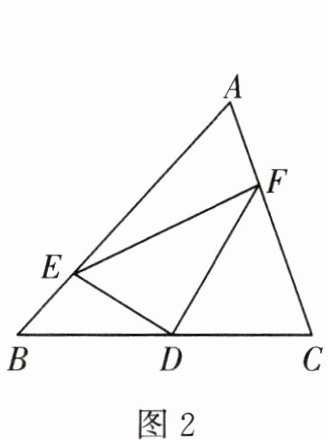
如图2,在$△ABC$中,D是BC边上的中点,$DE⊥DF$,DE交AB于点E,DF交AC于点F,连接EF.
(1)求证:$BE+CF>EF$.
(2)若$∠A= 90^{\circ }$,探索线段BE,CF,EF之间的等量关系,并加以证明.


解决方法:延长AD到E,使得$DE= AD$,再连接BE,可得$BE= AC$.把AB,AC,2AD集中在$△ABE$中,利用三角形的三边关系可得$2<AE<8$,则$1<AD<4$.
迁移应用:请参考上述解题方法,证明下列命题.
如图2,在$△ABC$中,D是BC边上的中点,$DE⊥DF$,DE交AB于点E,DF交AC于点F,连接EF.
(1)求证:$BE+CF>EF$.
(2)若$∠A= 90^{\circ }$,探索线段BE,CF,EF之间的等量关系,并加以证明.
答案:
【解析】:
(1) 本题可通过延长$FD$至点$G$,使$DG = DF$,连接$BG$、$EG$,利用三角形全等将$BE$、$CF$、$EF$转化到同一个三角形中,再根据三角形三边关系来证明$BE + CF>EF$。
(2) 当$\angle A = 90^{\circ}$时,可通过证明三角形全等得到对应边相等,再结合勾股定理来探索线段$BE$、$CF$、$EF$之间的等量关系。
【答案】:
(1) 证明:
延长$FD$至点$G$,使$DG = DF$,连接$BG$、$EG$。
因为$D$是$BC$边上的中点,所以$BD = CD$。
在$\triangle BDG$和$\triangle CDF$中,
$\begin{cases}BD = CD\\\angle BDG = \angle CDF\\DG = DF\end{cases}$
所以$\triangle BDG\cong\triangle CDF(SAS)$,则$BG = CF$。
因为$DE\perp DF$,$DG = DF$,所以$EG = EF$。
在$\triangle BEG$中,根据三角形三边关系:两边之和大于第三边,可得$BE + BG>EG$。
又因为$BG = CF$,$EG = EF$,所以$BE + CF>EF$。
(2) 若$\angle A = 90^{\circ}$,则$BE^{2}+CF^{2}=EF^{2}$。
证明:
由
(1)可知$\triangle BDG\cong\triangle CDF$,所以$\angle DBG = \angle C$,$BG = CF$。
因为$\angle A = 90^{\circ}$,所以$\angle ABC + \angle C = 90^{\circ}$,则$\angle ABC + \angle DBG = 90^{\circ}$,即$\angle EBG = 90^{\circ}$。
在$Rt\triangle EBG$中,根据勾股定理可得$BE^{2}+BG^{2}=EG^{2}$。
又因为$BG = CF$,$EG = EF$,所以$BE^{2}+CF^{2}=EF^{2}$。
(1) 本题可通过延长$FD$至点$G$,使$DG = DF$,连接$BG$、$EG$,利用三角形全等将$BE$、$CF$、$EF$转化到同一个三角形中,再根据三角形三边关系来证明$BE + CF>EF$。
(2) 当$\angle A = 90^{\circ}$时,可通过证明三角形全等得到对应边相等,再结合勾股定理来探索线段$BE$、$CF$、$EF$之间的等量关系。
【答案】:
(1) 证明:
延长$FD$至点$G$,使$DG = DF$,连接$BG$、$EG$。
因为$D$是$BC$边上的中点,所以$BD = CD$。
在$\triangle BDG$和$\triangle CDF$中,
$\begin{cases}BD = CD\\\angle BDG = \angle CDF\\DG = DF\end{cases}$
所以$\triangle BDG\cong\triangle CDF(SAS)$,则$BG = CF$。
因为$DE\perp DF$,$DG = DF$,所以$EG = EF$。
在$\triangle BEG$中,根据三角形三边关系:两边之和大于第三边,可得$BE + BG>EG$。
又因为$BG = CF$,$EG = EF$,所以$BE + CF>EF$。
(2) 若$\angle A = 90^{\circ}$,则$BE^{2}+CF^{2}=EF^{2}$。
证明:
由
(1)可知$\triangle BDG\cong\triangle CDF$,所以$\angle DBG = \angle C$,$BG = CF$。
因为$\angle A = 90^{\circ}$,所以$\angle ABC + \angle C = 90^{\circ}$,则$\angle ABC + \angle DBG = 90^{\circ}$,即$\angle EBG = 90^{\circ}$。
在$Rt\triangle EBG$中,根据勾股定理可得$BE^{2}+BG^{2}=EG^{2}$。
又因为$BG = CF$,$EG = EF$,所以$BE^{2}+CF^{2}=EF^{2}$。
查看更多完整答案,请扫码查看


