6. 如图,在四边形 ABCD 中,$AB// DC,AD= BC= $$5,DC= 7,AB= 13$,点 P 从点 A 出发以 3 个单位长度/s 的速度沿$AD→DC$向终点 C 运动,同时点 Q 从点 B 出发,以 1 个单位长度/s 的速度沿 BA 向终点 A 运动. 当四边形 PQBC 为平行四边形时,运动时间为____.


3
答案:
解:设运动时间为 $ t $ 秒。
点 $ P $ 从 $ A $ 出发沿 $ AD→DC $ 运动,速度为 3 单位/s,$ AD = 5 $,则:
当 $ 0 \leq t \leq \frac{5}{3} $ 时,$ P $ 在 $ AD $ 上,$ PD = 5 - 3t $,此时 $ PC $ 不与 $ BQ $ 平行,四边形 $ PQBC $ 不可能为平行四边形。
当 $ t > \frac{5}{3} $ 时,$ P $ 在 $ DC $ 上,$ PC = DC - (3t - AD) = 7 - (3t - 5) = 12 - 3t $。
点 $ Q $ 从 $ B $ 出发沿 $ BA $ 向 $ A $ 运动,速度为 1 单位/s,$ BQ = t $。
因为 $ AB // DC $,要使四边形 $ PQBC $ 为平行四边形,需 $ PC = BQ $,即:
$ 12 - 3t = t $
解得 $ t = 3 $。
此时 $ t = 3 > \frac{5}{3} $,符合 $ P $ 在 $ DC $ 上的条件。
答:3。
点 $ P $ 从 $ A $ 出发沿 $ AD→DC $ 运动,速度为 3 单位/s,$ AD = 5 $,则:
当 $ 0 \leq t \leq \frac{5}{3} $ 时,$ P $ 在 $ AD $ 上,$ PD = 5 - 3t $,此时 $ PC $ 不与 $ BQ $ 平行,四边形 $ PQBC $ 不可能为平行四边形。
当 $ t > \frac{5}{3} $ 时,$ P $ 在 $ DC $ 上,$ PC = DC - (3t - AD) = 7 - (3t - 5) = 12 - 3t $。
点 $ Q $ 从 $ B $ 出发沿 $ BA $ 向 $ A $ 运动,速度为 1 单位/s,$ BQ = t $。
因为 $ AB // DC $,要使四边形 $ PQBC $ 为平行四边形,需 $ PC = BQ $,即:
$ 12 - 3t = t $
解得 $ t = 3 $。
此时 $ t = 3 > \frac{5}{3} $,符合 $ P $ 在 $ DC $ 上的条件。
答:3。
7. 如图,E 是正方形 ABCD 的对角线 BD 上的点,连接 AE,CE.
(1)求证:$AE= CE.$
(2)若将$△ABE$沿 AB 翻折后得到$△ABF$,当点 E 在 BD 的何处时,四边形 AFBE 是正方形? 请证明你的结论.
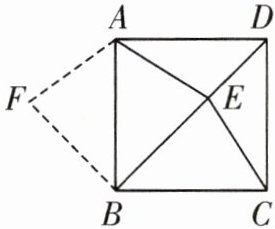
(1)求证:$AE= CE.$
(2)若将$△ABE$沿 AB 翻折后得到$△ABF$,当点 E 在 BD 的何处时,四边形 AFBE 是正方形? 请证明你的结论.

答案:
(1)证明:
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,
在△ABE和△CBE中,
$\left\{\begin{array}{l} AB=CB\\ ∠ABE=∠CBE\\ BE=BE\end{array}\right.$,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)当点E是BD的中点时,四边形AFBE是正方形,
证明:
∵四边形ABCD是正方形,E是BD的中点,
∴AE⊥BD,AE=BE,
∵将△ABE沿AB翻折后得到△ABF,
∴AF=AE,BF=BE,∠FAB=∠EAB=45°,∠FBA=∠EBA=45°,
∴AF=BF=BE=AE,∠F=∠AEB=90°,
∴四边形AFBE是菱形,
∵∠F=90°,
∴四边形AFBE是正方形。
(1)证明:
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,
在△ABE和△CBE中,
$\left\{\begin{array}{l} AB=CB\\ ∠ABE=∠CBE\\ BE=BE\end{array}\right.$,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)当点E是BD的中点时,四边形AFBE是正方形,
证明:
∵四边形ABCD是正方形,E是BD的中点,
∴AE⊥BD,AE=BE,
∵将△ABE沿AB翻折后得到△ABF,
∴AF=AE,BF=BE,∠FAB=∠EAB=45°,∠FBA=∠EBA=45°,
∴AF=BF=BE=AE,∠F=∠AEB=90°,
∴四边形AFBE是菱形,
∵∠F=90°,
∴四边形AFBE是正方形。
探索规律并解决问题.
(1)如图 1,试探究$∠1,∠2与∠3,∠4$之间的数量关系.
(2)请你用文字描述上述的关系.
(3)用你发现的结论解决下列问题.
如图 2,AE,DE 分别是四边形 ABCD 的外角$∠NAD,∠MDA$的平分线,$∠B+$$∠C= 240^{\circ }$,求$∠E$的度数.
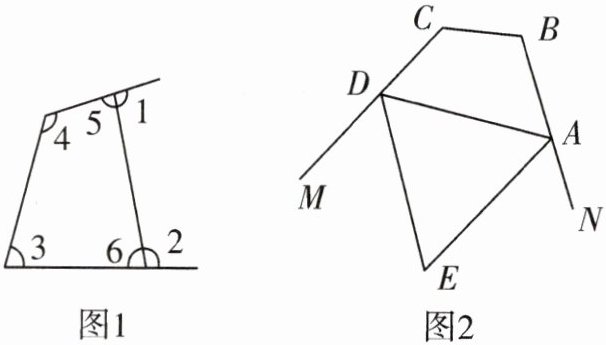
(1)如图 1,试探究$∠1,∠2与∠3,∠4$之间的数量关系.
(2)请你用文字描述上述的关系.
(3)用你发现的结论解决下列问题.
如图 2,AE,DE 分别是四边形 ABCD 的外角$∠NAD,∠MDA$的平分线,$∠B+$$∠C= 240^{\circ }$,求$∠E$的度数.

答案:
(1)解:连接图1中两个外角的顶点,形成两个三角形。在上方三角形中,∠1=∠5+∠6;在下方四边形中,∠3+∠4+∠5+∠6=360°,则∠5+∠6=360°-∠3-∠4,所以∠1+∠2=∠5+∠6+180°=360°-∠3-∠4+180°=540°-∠3-∠4,即∠1+∠2+∠3+∠4=540°。
(2)解:四边形的两个外角与另外两个内角的和为540°。
(3)解:在四边形ABCD中,∠B+∠C=240°,由
(2)结论知∠NAD+∠MDA+∠B+∠C=540°,则∠NAD+∠MDA=540°-240°=300°。因为AE、DE是角平分线,所以∠EAD=∠NAD/2,∠EDA=∠MDA/2,∠EAD+∠EDA=300°/2=150°,在△ADE中,∠E=180°-150°=30°。
(1)∠1+∠2+∠3+∠4=540°;
(2)四边形的两个外角与另外两个内角的和为540°;
(3)30°
(1)解:连接图1中两个外角的顶点,形成两个三角形。在上方三角形中,∠1=∠5+∠6;在下方四边形中,∠3+∠4+∠5+∠6=360°,则∠5+∠6=360°-∠3-∠4,所以∠1+∠2=∠5+∠6+180°=360°-∠3-∠4+180°=540°-∠3-∠4,即∠1+∠2+∠3+∠4=540°。
(2)解:四边形的两个外角与另外两个内角的和为540°。
(3)解:在四边形ABCD中,∠B+∠C=240°,由
(2)结论知∠NAD+∠MDA+∠B+∠C=540°,则∠NAD+∠MDA=540°-240°=300°。因为AE、DE是角平分线,所以∠EAD=∠NAD/2,∠EDA=∠MDA/2,∠EAD+∠EDA=300°/2=150°,在△ADE中,∠E=180°-150°=30°。
(1)∠1+∠2+∠3+∠4=540°;
(2)四边形的两个外角与另外两个内角的和为540°;
(3)30°
查看更多完整答案,请扫码查看


