1. 历史上对勾股定理的一种证法采用了如图所示的图形,其中两个全等的直角三角形的边AE,EB在一条直线上.该证法用到的面积相等关系是 (
A.$S_{△EDA}= S_{△CEB}$
B.$S_{△EDA}+S_{△CEB}= S_{△CDE}$
C.$S_{四边形CDAE}= S_{四边形CDEB}$
D.$S_{△EDA}+S_{△CDE}+S_{△CEB}= S_{四边形ABCD}$
D
)A.$S_{△EDA}= S_{△CEB}$
B.$S_{△EDA}+S_{△CEB}= S_{△CDE}$
C.$S_{四边形CDAE}= S_{四边形CDEB}$
D.$S_{△EDA}+S_{△CDE}+S_{△CEB}= S_{四边形ABCD}$
答案:
【解析】:
首先,观察图形,我们可以看到有两个全等的直角三角形$\triangle ADE$和$\triangle BEC$。
第一步,根据直角三角形的全等性质,我们知道如果两个直角三角形全等,那么它们的对应边和对应角都相等。
第二步,由于$\triangle ADE \cong \triangle BEC$,我们可以得到$AD = BE$,$AE = BC$,且$\angle ADE = \angle BEC$。
第三步,考虑选项中的面积关系。
A选项:$S_{\triangle EDA} = S_{\triangle CEB}$。这个选项只考虑了两个全等的直角三角形的面积,没有涉及其他部分,所以不能直接证明勾股定理。
B选项:$S_{\triangle EDA} + S_{\triangle CEB} = S_{\triangle CDE}$。这个选项没有考虑四边形$ABCD$的面积,也不能直接证明勾股定理。
C选项:$S_{四边形CDAE} = S_{四边形CDEB}$。这个选项错误地认为两个由全等直角三角形和公共边构成的四边形面积相等,但实际上这两个四边形的面积并不相等。
D选项:$S_{\triangle EDA} + S_{\triangle CDE} + S_{\triangle CEB} = S_{四边形ABCD}$。这个选项正确地表示了整个四边形$ABCD$的面积可以由三个三角形的面积之和来表示。
第四步,根据勾股定理的证明方法,我们知道可以通过证明两个直角三角形的面积和与某个四边形的面积关系来推导出勾股定理。在这里,选项D正确地表示了这种关系。
第五步,进一步分析,我们可以将$S_{\triangle EDA}$,$S_{\triangle CDE}$,和$S_{\triangle CEB}$分别用直角三角形的边长来表示,并通过代数运算来推导出勾股定理。但这一步在选择题中并不需要详细展开,只需确认选项D是正确的面积关系即可。
综上,答案是D。
【答案】:D
首先,观察图形,我们可以看到有两个全等的直角三角形$\triangle ADE$和$\triangle BEC$。
第一步,根据直角三角形的全等性质,我们知道如果两个直角三角形全等,那么它们的对应边和对应角都相等。
第二步,由于$\triangle ADE \cong \triangle BEC$,我们可以得到$AD = BE$,$AE = BC$,且$\angle ADE = \angle BEC$。
第三步,考虑选项中的面积关系。
A选项:$S_{\triangle EDA} = S_{\triangle CEB}$。这个选项只考虑了两个全等的直角三角形的面积,没有涉及其他部分,所以不能直接证明勾股定理。
B选项:$S_{\triangle EDA} + S_{\triangle CEB} = S_{\triangle CDE}$。这个选项没有考虑四边形$ABCD$的面积,也不能直接证明勾股定理。
C选项:$S_{四边形CDAE} = S_{四边形CDEB}$。这个选项错误地认为两个由全等直角三角形和公共边构成的四边形面积相等,但实际上这两个四边形的面积并不相等。
D选项:$S_{\triangle EDA} + S_{\triangle CDE} + S_{\triangle CEB} = S_{四边形ABCD}$。这个选项正确地表示了整个四边形$ABCD$的面积可以由三个三角形的面积之和来表示。
第四步,根据勾股定理的证明方法,我们知道可以通过证明两个直角三角形的面积和与某个四边形的面积关系来推导出勾股定理。在这里,选项D正确地表示了这种关系。
第五步,进一步分析,我们可以将$S_{\triangle EDA}$,$S_{\triangle CDE}$,和$S_{\triangle CEB}$分别用直角三角形的边长来表示,并通过代数运算来推导出勾股定理。但这一步在选择题中并不需要详细展开,只需确认选项D是正确的面积关系即可。
综上,答案是D。
【答案】:D
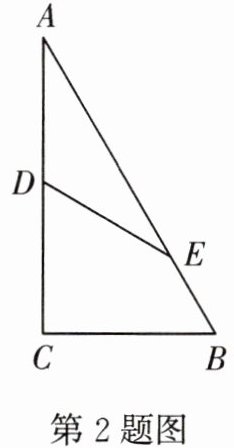
2. 如图,已知在$Rt△ABC$中,$∠C= 90^{\circ },∠A= 30^{\circ },AB= 4$,点D,E分别在边AC,AB上.若$AD= DC,AE= CB+BE$,则线段DE的长为 (
A.$2\sqrt {3}-2$
B.$\sqrt {3}$
C.$\frac {\sqrt {3}}{2}+1$
D.2
B
)
A.$2\sqrt {3}-2$
B.$\sqrt {3}$
C.$\frac {\sqrt {3}}{2}+1$
D.2
答案:
解:在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$\angle A=30^{\circ}$,$AB=4$,
$\therefore BC=\frac{1}{2}AB=2$,$AC=AB\cos30^{\circ}=4×\frac{\sqrt{3}}{2}=2\sqrt{3}$。
设$BE=x$,则$AE=CB+BE=2+x$,
$\because AE+BE=AB$,$\therefore 2+x+x=4$,解得$x=1$,$\therefore AE=3$。
$\because AD=DC$,$\therefore AD=\frac{1}{2}AC=\sqrt{3}$。
过点$E$作$EF\perp AC$于点$F$,
在$Rt\triangle AEF$中,$\angle A=30^{\circ}$,$AE=3$,
$\therefore EF=\frac{1}{2}AE=\frac{3}{2}$,$AF=AE\cos30^{\circ}=3×\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}$。
$\because AD=\sqrt{3}$,$\therefore DF=AF - AD=\frac{3\sqrt{3}}{2}-\sqrt{3}=\frac{\sqrt{3}}{2}$。
在$Rt\triangle DEF$中,$DE=\sqrt{DF^{2}+EF^{2}}=\sqrt{(\frac{\sqrt{3}}{2})^{2}+(\frac{3}{2})^{2}}=\sqrt{\frac{3}{4}+\frac{9}{4}}=\sqrt{3}$。
答案:B
$\therefore BC=\frac{1}{2}AB=2$,$AC=AB\cos30^{\circ}=4×\frac{\sqrt{3}}{2}=2\sqrt{3}$。
设$BE=x$,则$AE=CB+BE=2+x$,
$\because AE+BE=AB$,$\therefore 2+x+x=4$,解得$x=1$,$\therefore AE=3$。
$\because AD=DC$,$\therefore AD=\frac{1}{2}AC=\sqrt{3}$。
过点$E$作$EF\perp AC$于点$F$,
在$Rt\triangle AEF$中,$\angle A=30^{\circ}$,$AE=3$,
$\therefore EF=\frac{1}{2}AE=\frac{3}{2}$,$AF=AE\cos30^{\circ}=3×\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}$。
$\because AD=\sqrt{3}$,$\therefore DF=AF - AD=\frac{3\sqrt{3}}{2}-\sqrt{3}=\frac{\sqrt{3}}{2}$。
在$Rt\triangle DEF$中,$DE=\sqrt{DF^{2}+EF^{2}}=\sqrt{(\frac{\sqrt{3}}{2})^{2}+(\frac{3}{2})^{2}}=\sqrt{\frac{3}{4}+\frac{9}{4}}=\sqrt{3}$。
答案:B
3. 如图,长方形OBPC的边OB长为3,边OC长为2,OC在数轴上,以原点O为圆心,以OP的长为半径画弧,交数轴的负半轴于点A,则点A表示的数介于 (
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
A
)A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
答案:
【解析】:本题可先根据长方形的性质和勾股定理求出$OP$的长度,再结合点$A$的位置确定点$A$表示的数的范围。
步骤一:求$OP$的长度
在长方形$OBPC$中,$\angle OCP = 90^{\circ}$,$OB = 3$,$OC = 2$,因为长方形的对边相等,所以$CP = OB = 3$。
在$Rt\triangle OCP$中,根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),可得$OP=\sqrt{OC^{2}+CP^{2}}$。
将$OC = 2$,$CP = 3$代入上式可得:$OP=\sqrt{2^{2}+3^{2}}=\sqrt{4 + 9}=\sqrt{13}$。
步骤二:确定点$A$表示的数的范围
因为以原点$O$为圆心,以$OP$的长为半径画弧交数轴的负半轴于点$A$,所以$OA = OP=\sqrt{13}$。
由于$9\lt 13\lt 16$,根据算术平方根的性质,被开方数越大,其算术平方根越大,可得$\sqrt{9}\lt\sqrt{13}\lt\sqrt{16}$,即$3\lt\sqrt{13}\lt 4$。
因为点$A$在数轴的负半轴,所以点$A$表示的数为$-\sqrt{13}$,那么$-4\lt -\sqrt{13}\lt -3$,即点$A$表示的数介于$-4$和$-3$之间。
【答案】:A
步骤一:求$OP$的长度
在长方形$OBPC$中,$\angle OCP = 90^{\circ}$,$OB = 3$,$OC = 2$,因为长方形的对边相等,所以$CP = OB = 3$。
在$Rt\triangle OCP$中,根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),可得$OP=\sqrt{OC^{2}+CP^{2}}$。
将$OC = 2$,$CP = 3$代入上式可得:$OP=\sqrt{2^{2}+3^{2}}=\sqrt{4 + 9}=\sqrt{13}$。
步骤二:确定点$A$表示的数的范围
因为以原点$O$为圆心,以$OP$的长为半径画弧交数轴的负半轴于点$A$,所以$OA = OP=\sqrt{13}$。
由于$9\lt 13\lt 16$,根据算术平方根的性质,被开方数越大,其算术平方根越大,可得$\sqrt{9}\lt\sqrt{13}\lt\sqrt{16}$,即$3\lt\sqrt{13}\lt 4$。
因为点$A$在数轴的负半轴,所以点$A$表示的数为$-\sqrt{13}$,那么$-4\lt -\sqrt{13}\lt -3$,即点$A$表示的数介于$-4$和$-3$之间。
【答案】:A
4. 已知,在$Rt△ABC$中,$∠C= 90^{\circ }$,AD平分$∠BAC$交BC于点D,若$BC= 32$,且$BD:CD= 9:7$,则D到AB的距离为 (
A.18
B.16
C.14
D.12
C
)A.18
B.16
C.14
D.12
答案:
【解析】:
本题主要考查了角平分线的性质以及角的平分线定理的逆定理,即角平分线上的点到角的两边的距离相等。
首先,根据题目给出的$BD:CD=9:7$,以及$BC=32$,可以计算出$CD$的长度。
设$CD=7x$,$BD=9x$,则有$7x+9x=32$,
解得$x=2$,
所以$CD=7× 2=14$。
由于$AD$平分$\angle BAC$,根据角平分线的性质,点$D$到$AB$的距离等于$D$到$AC$的距离。
在直角三角形$ABC$中,由于$\angle C=90^{\circ}$,所以$D$到$AC$的距离就是$CD$的长度,即$14$。
因此,$D$到$AB$的距离也是$14$。
【答案】:
C. $14$。
本题主要考查了角平分线的性质以及角的平分线定理的逆定理,即角平分线上的点到角的两边的距离相等。
首先,根据题目给出的$BD:CD=9:7$,以及$BC=32$,可以计算出$CD$的长度。
设$CD=7x$,$BD=9x$,则有$7x+9x=32$,
解得$x=2$,
所以$CD=7× 2=14$。
由于$AD$平分$\angle BAC$,根据角平分线的性质,点$D$到$AB$的距离等于$D$到$AC$的距离。
在直角三角形$ABC$中,由于$\angle C=90^{\circ}$,所以$D$到$AC$的距离就是$CD$的长度,即$14$。
因此,$D$到$AB$的距离也是$14$。
【答案】:
C. $14$。
5. 如右图,在等边三角形ABC中,D是AB的中点,$DE⊥AC$于点E,$EF⊥BC$于点F.已知$AB= 8$,则BF的长为
5
.
答案:
【解析】:本题可先根据等边三角
形的性质求出$AD$的长度,再在直角三角形$ADE$中求出$AE$的长度,进而得到$EC$的长度,最后在直角三角形$EFC$中求出$BF$的长度。
已知$\triangle ABC$是等边三角形,$AB = 8$,$D$是$AB$的中点,则$AD=\frac{1}{2}AB = \frac{1}{2}×8 = 4$。
因为$\triangle ABC$是等边三角形,所以$\angle A = 60^{\circ}$。
又因为$DE\perp AC$,所以$\angle AED = 90^{\circ}$,在$Rt\triangle ADE$中,$\angle ADE = 180^{\circ} - 90^{\circ} - 60^{\circ} = 30^{\circ}$。
在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半,所以$AE = \frac{1}{2}AD = \frac{1}{2}×4 = 2$。
则$EC = AC - AE = 8 - 2 = 6$。
因为$\triangle ABC$是等边三角形,所以$\angle C = 60^{\circ}$,又因为$EF\perp BC$,所以$\angle FEC = 90^{\circ}$,在$Rt\triangle EFC$中,$\angle FEC = 30^{\circ}$。
同样根据在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半,可得$FC = \frac{1}{2}EC = \frac{1}{2}×6 = 3$。
因为$BC = 8$,所以$BF = BC - FC = 8 - 3 = 5$。
【答案】:$5$
形的性质求出$AD$的长度,再在直角三角形$ADE$中求出$AE$的长度,进而得到$EC$的长度,最后在直角三角形$EFC$中求出$BF$的长度。
已知$\triangle ABC$是等边三角形,$AB = 8$,$D$是$AB$的中点,则$AD=\frac{1}{2}AB = \frac{1}{2}×8 = 4$。
因为$\triangle ABC$是等边三角形,所以$\angle A = 60^{\circ}$。
又因为$DE\perp AC$,所以$\angle AED = 90^{\circ}$,在$Rt\triangle ADE$中,$\angle ADE = 180^{\circ} - 90^{\circ} - 60^{\circ} = 30^{\circ}$。
在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半,所以$AE = \frac{1}{2}AD = \frac{1}{2}×4 = 2$。
则$EC = AC - AE = 8 - 2 = 6$。
因为$\triangle ABC$是等边三角形,所以$\angle C = 60^{\circ}$,又因为$EF\perp BC$,所以$\angle FEC = 90^{\circ}$,在$Rt\triangle EFC$中,$\angle FEC = 30^{\circ}$。
同样根据在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半,可得$FC = \frac{1}{2}EC = \frac{1}{2}×6 = 3$。
因为$BC = 8$,所以$BF = BC - FC = 8 - 3 = 5$。
【答案】:$5$
查看更多完整答案,请扫码查看


