1.三角形的三边长度如下:
①$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$;②$3^2$,$4^2$,$5^2$;③9x,40x,41x(x>0);④$(m+n)^2-1$,2(m+n),$(m+n)^2+1$(m+n>1).
其中能构成直角三角形的有 (
A.1个
B.2个
C.3个
D.4个
①$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$;②$3^2$,$4^2$,$5^2$;③9x,40x,41x(x>0);④$(m+n)^2-1$,2(m+n),$(m+n)^2+1$(m+n>1).
其中能构成直角三角形的有 (
B
)A.1个
B.2个
C.3个
D.4个
答案:
【解析】:
本题主要考察勾股定理的逆定理,即如果三角形三边满足$a^2 + b^2 = c^2$,则这个三角形是直角三角形。
对于①:计算较小两边的平方和与最长边的平方:
$(\frac{1}{4})^2 + (\frac{1}{5})^2 = \frac{1}{16} + \frac{1}{25} = \frac{41}{400}$
$(\frac{1}{3})^2 = \frac{1}{9} = \frac{44}{400} - \frac{3}{400} \ne \frac{41}{400}$
因为$\frac{41}{400} \ne \frac{44}{400} - \frac{3}{400}$,所以①不能构成直角三角形。
对于②:计算较小两边的平方和与最长边的平方:
$3^4 + 4^4 = 81 + 256 = 337$
$5^4 = 625$
因为$337 \ne 625$,所以②不能构成直角三角形。
实际上,这里应该是考虑$3^2, 4^2, 5^2$作为边长,但即使这样,$9+16=25$,但边长是$9,16,25$,显然不能构成三角形,更不用说直角三角形了。原题中的$3^2, 4^2, 5^2$应理解为边长的平方,而非边长本身。
对于③:计算较小两边的平方和与最长边的平方:
$(9x)^2 + (40x)^2 = 81x^2 + 1600x^2 = 1681x^2$
$(41x)^2 = 1681x^2$
因为两者相等,所以③能构成直角三角形。
对于④:计算较小两边的平方和与最长边的平方:
$[2(m+n)]^2 + [(m+n)^2 - 1]^2 = 4(m+n)^2 + (m+n)^4 - 2(m+n)^2 + 1 = (m+n)^4 + 2(m+n)^2 + 1$
$[(m+n)^2 + 1]^2 = (m+n)^4 + 2(m+n)^2 + 1$
因为两者相等,所以④能构成直角三角形。
综上,能构成直角三角形的有2个。
【答案】:B.2个。
本题主要考察勾股定理的逆定理,即如果三角形三边满足$a^2 + b^2 = c^2$,则这个三角形是直角三角形。
对于①:计算较小两边的平方和与最长边的平方:
$(\frac{1}{4})^2 + (\frac{1}{5})^2 = \frac{1}{16} + \frac{1}{25} = \frac{41}{400}$
$(\frac{1}{3})^2 = \frac{1}{9} = \frac{44}{400} - \frac{3}{400} \ne \frac{41}{400}$
因为$\frac{41}{400} \ne \frac{44}{400} - \frac{3}{400}$,所以①不能构成直角三角形。
对于②:计算较小两边的平方和与最长边的平方:
$3^4 + 4^4 = 81 + 256 = 337$
$5^4 = 625$
因为$337 \ne 625$,所以②不能构成直角三角形。
实际上,这里应该是考虑$3^2, 4^2, 5^2$作为边长,但即使这样,$9+16=25$,但边长是$9,16,25$,显然不能构成三角形,更不用说直角三角形了。原题中的$3^2, 4^2, 5^2$应理解为边长的平方,而非边长本身。
对于③:计算较小两边的平方和与最长边的平方:
$(9x)^2 + (40x)^2 = 81x^2 + 1600x^2 = 1681x^2$
$(41x)^2 = 1681x^2$
因为两者相等,所以③能构成直角三角形。
对于④:计算较小两边的平方和与最长边的平方:
$[2(m+n)]^2 + [(m+n)^2 - 1]^2 = 4(m+n)^2 + (m+n)^4 - 2(m+n)^2 + 1 = (m+n)^4 + 2(m+n)^2 + 1$
$[(m+n)^2 + 1]^2 = (m+n)^4 + 2(m+n)^2 + 1$
因为两者相等,所以④能构成直角三角形。
综上,能构成直角三角形的有2个。
【答案】:B.2个。
2.如图所示,若AB//CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于E,且PE= 3cm,则AB与CD之间的距离为 (
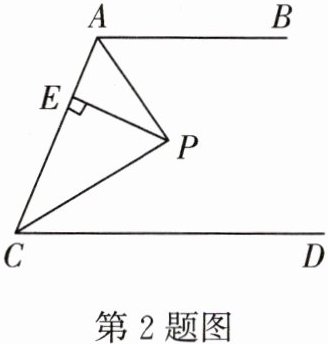
A.3cm
B.6cm
C.9cm
D.无法确定
B
)
A.3cm
B.6cm
C.9cm
D.无法确定
答案:
【解析】:本题可根据角平分线的性质以及平行线的性质,通过作辅助线来求解$AB$与$CD$之间的距离。
步骤一:过点$P$作$PF\perp AB$于$F$,作$PG\perp CD$于$G$。
因为$AP$平分$\angle BAC$,$PE\perp AC$,$PF\perp AB$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$PF = PE$。
同理,因为$CP$平分$\angle ACD$,$PE\perp AC$,$PG\perp CD$,所以$PG = PE$。
步骤二:求出$PF$和$PG$的长度。
已知$PE = 3cm$,由$PF = PE$,$PG = PE$,可得$PF = PG = 3cm$。
步骤三:分析$AB$与$CD$之间的距离。
因为$AB// CD$,$PF\perp AB$,$PG\perp CD$,所以$AB$与$CD$之间的距离就等于$PF + PG$。
将$PF = 3cm$,$PG = 3cm$代入$PF + PG$,可得$3 + 3 = 6cm$。
【答案】:B
步骤一:过点$P$作$PF\perp AB$于$F$,作$PG\perp CD$于$G$。
因为$AP$平分$\angle BAC$,$PE\perp AC$,$PF\perp AB$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$PF = PE$。
同理,因为$CP$平分$\angle ACD$,$PE\perp AC$,$PG\perp CD$,所以$PG = PE$。
步骤二:求出$PF$和$PG$的长度。
已知$PE = 3cm$,由$PF = PE$,$PG = PE$,可得$PF = PG = 3cm$。
步骤三:分析$AB$与$CD$之间的距离。
因为$AB// CD$,$PF\perp AB$,$PG\perp CD$,所以$AB$与$CD$之间的距离就等于$PF + PG$。
将$PF = 3cm$,$PG = 3cm$代入$PF + PG$,可得$3 + 3 = 6cm$。
【答案】:B
3.如图,▱ABCD的对角线AC与BD相交于点O,OE⊥BC,垂足为E,AB= $\sqrt{5}$,AC= 4,BD= 6,则OE的长为 (
A.$\frac{3}{2}$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{2\sqrt{105}}{21}$
D.$\frac{4\sqrt{105}}{21}$
D
)A.$\frac{3}{2}$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{2\sqrt{105}}{21}$
D.$\frac{4\sqrt{105}}{21}$
答案:
解:
∵四边形ABCD是平行四边形,AC=4,BD=6,
∴OA=OC=2,OB=OD=3,AB=CD=√5,AD=BC。
在△AOB中,OA=2,OB=3,AB=√5,
∵OA²+AB²=2²+(√5)²=4+5=9=OB²,
∴△AOB是直角三角形,∠OAB=90°。
平行四边形ABCD的面积=AB·AC=√5×4=4√5。
∵OE⊥BC,
∴S▱ABCD=BC·OE=4√5。
在Rt△ABC中,AB=√5,AC=4,
∴BC=√(AB²+AC²)=√[(√5)²+4²]=√(5+16)=√21。
∴OE=4√5/BC=4√5/√21=4√105/21。
答案:D
∵四边形ABCD是平行四边形,AC=4,BD=6,
∴OA=OC=2,OB=OD=3,AB=CD=√5,AD=BC。
在△AOB中,OA=2,OB=3,AB=√5,
∵OA²+AB²=2²+(√5)²=4+5=9=OB²,
∴△AOB是直角三角形,∠OAB=90°。
平行四边形ABCD的面积=AB·AC=√5×4=4√5。
∵OE⊥BC,
∴S▱ABCD=BC·OE=4√5。
在Rt△ABC中,AB=√5,AC=4,
∴BC=√(AB²+AC²)=√[(√5)²+4²]=√(5+16)=√21。
∴OE=4√5/BC=4√5/√21=4√105/21。
答案:D
4.在▱ABCD中,AE平分∠BAD,且分边BC为3和4两部分,则▱ABCD的周长为
20或22
.
答案:
解:
∵四边形ABCD是平行四边形,
∴AD//BC,AB=CD,AD=BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
情况一:当BE=3,EC=4时,
AB=BE=3,BC=BE+EC=3+4=7,
▱ABCD的周长为2×(AB+BC)=2×(3+7)=20;
情况二:当BE=4,EC=3时,
AB=BE=4,BC=BE+EC=4+3=7,
▱ABCD的周长为2×(AB+BC)=2×(4+7)=22;
综上,▱ABCD的周长为20或22。
∵四边形ABCD是平行四边形,
∴AD//BC,AB=CD,AD=BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
情况一:当BE=3,EC=4时,
AB=BE=3,BC=BE+EC=3+4=7,
▱ABCD的周长为2×(AB+BC)=2×(3+7)=20;
情况二:当BE=4,EC=3时,
AB=BE=4,BC=BE+EC=4+3=7,
▱ABCD的周长为2×(AB+BC)=2×(4+7)=22;
综上,▱ABCD的周长为20或22。
5.点O是△ABC内一点,且到三边的距离相等.若∠A= 50°,则∠BOC的度数为
115°
.
答案:
【解析】:
本题主要考察的是角平分线的性质以及三角形内角和定理。
由于点$O$到$\bigtriangleup ABC$三边的距离相等,根据角平分线的性质(到角两边距离相等的点在这个角的平分线上),我们可以知道点$O$是$\angle ABC$和$\angle ACB$的角平分线的交点。
接下来,我们需要求出$\angle BOC$的度数。
由于$\angle A = 50^\circ$,根据三角形内角和定理(三角形的内角和等于$180^\circ$),我们可以求出$\angle ABC + \angle ACB = 180^\circ - 50^\circ = 130^\circ$。
由于$O$是$\angle ABC$和$\angle ACB$的角平分线的交点,所以$\angle OBC = \frac{1}{2} \angle ABC$,$\angle OCB = \frac{1}{2} \angle ACB$。
因此,$\angle BOC = 180^\circ - (\angle OBC + \angle OCB) = 180^\circ - \frac{1}{2}(\angle ABC + \angle ACB) = 180^\circ - \frac{1}{2} × 130^\circ = 115^\circ$。
【答案】:
$115^\circ$
本题主要考察的是角平分线的性质以及三角形内角和定理。
由于点$O$到$\bigtriangleup ABC$三边的距离相等,根据角平分线的性质(到角两边距离相等的点在这个角的平分线上),我们可以知道点$O$是$\angle ABC$和$\angle ACB$的角平分线的交点。
接下来,我们需要求出$\angle BOC$的度数。
由于$\angle A = 50^\circ$,根据三角形内角和定理(三角形的内角和等于$180^\circ$),我们可以求出$\angle ABC + \angle ACB = 180^\circ - 50^\circ = 130^\circ$。
由于$O$是$\angle ABC$和$\angle ACB$的角平分线的交点,所以$\angle OBC = \frac{1}{2} \angle ABC$,$\angle OCB = \frac{1}{2} \angle ACB$。
因此,$\angle BOC = 180^\circ - (\angle OBC + \angle OCB) = 180^\circ - \frac{1}{2}(\angle ABC + \angle ACB) = 180^\circ - \frac{1}{2} × 130^\circ = 115^\circ$。
【答案】:
$115^\circ$
6.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF= 12,AB= 10,则AE的长为
16
.
答案:
【解析】:本题考查了平行四边形的性质,角平分线的性质,等腰三角形的判定和勾股定理的运用。
由于$AE$是$\angle BAD$的平分线,
因此有$\angle BAE = \angle DAE$。
又因为四边形$ABCD$是平行四边形,
所以$AD // BC$,
根据两直线平行,内错角相等,
所以$\angle DAE = \angle AEB$,
由于$\angle BAE = \angle AEB$,
根据等腰三角形的性质,我们得出$AB = BE$。
同理,由于$BF$是$\angle ABC$的平分线,
我们有$\angle ABF = \angle CBF$。
又因为$AD // BC$,
所以$\angle AFB = \angle CBF$,
由于$\angle ABF = \angle AFB$,
我们得出$AB = AF$,即$AF = BE$。
所以四边形$ABEF$是平行四边形。
由于$AB = BE$,
所以四边形$ABEF$是菱形。
因此,$AE \perp BF$,且$AO = \frac{1}{2}AE$,$BO = \frac{1}{2}BF = 6$。
在直角三角形$AOB$中,根据勾股定理,我们有:
$AO = \sqrt{AB^{2} - BO^{2}} = \sqrt{10^{2} - 6^{2}} = 8$,
所以,$AE = 2AO = 16$。
【答案】:16。
由于$AE$是$\angle BAD$的平分线,
因此有$\angle BAE = \angle DAE$。
又因为四边形$ABCD$是平行四边形,
所以$AD // BC$,
根据两直线平行,内错角相等,
所以$\angle DAE = \angle AEB$,
由于$\angle BAE = \angle AEB$,
根据等腰三角形的性质,我们得出$AB = BE$。
同理,由于$BF$是$\angle ABC$的平分线,
我们有$\angle ABF = \angle CBF$。
又因为$AD // BC$,
所以$\angle AFB = \angle CBF$,
由于$\angle ABF = \angle AFB$,
我们得出$AB = AF$,即$AF = BE$。
所以四边形$ABEF$是平行四边形。
由于$AB = BE$,
所以四边形$ABEF$是菱形。
因此,$AE \perp BF$,且$AO = \frac{1}{2}AE$,$BO = \frac{1}{2}BF = 6$。
在直角三角形$AOB$中,根据勾股定理,我们有:
$AO = \sqrt{AB^{2} - BO^{2}} = \sqrt{10^{2} - 6^{2}} = 8$,
所以,$AE = 2AO = 16$。
【答案】:16。
查看更多完整答案,请扫码查看


