6. 将一些数据分成5组,第一、二、三组共有250个数,第三、四、五组共有230个数,若第三组的频率为0.2,则这些数据的总频数为.
答案:
【解析】:
题目考查了频率与频数的关系。
首先,根据题目描述,第一、二、三组共有250个数,第三、四、五组共有230个数。
设第三组的数据个数为$x$,那么第一、二组的数据总数为$250 - x$,第四、五组的数据总数为$230 - x$。
又因为第三组的频率为0.2,设总数据数为$N$,则有:
$\frac{x}{N} = 0.2$,
即$x = 0.2N$,
根据这个关系,可以得到第一、二、四、五组的数据总数为:
$N - x = N - 0.2N = 0.8N$,
根据题意,这个总数也等于第一、二组与第四、五组的和,即:
$250 - x + 230 - x = 0.8N$,
将$x = 0.2N$代入上式,得:
$250 - 0.2N + 230 - 0.2N = 0.8N$,
$480 - 0.4N = 0.8N$,
$480 = 1.2N$,
$N = 400$。
【答案】:
400。
题目考查了频率与频数的关系。
首先,根据题目描述,第一、二、三组共有250个数,第三、四、五组共有230个数。
设第三组的数据个数为$x$,那么第一、二组的数据总数为$250 - x$,第四、五组的数据总数为$230 - x$。
又因为第三组的频率为0.2,设总数据数为$N$,则有:
$\frac{x}{N} = 0.2$,
即$x = 0.2N$,
根据这个关系,可以得到第一、二、四、五组的数据总数为:
$N - x = N - 0.2N = 0.8N$,
根据题意,这个总数也等于第一、二组与第四、五组的和,即:
$250 - x + 230 - x = 0.8N$,
将$x = 0.2N$代入上式,得:
$250 - 0.2N + 230 - 0.2N = 0.8N$,
$480 - 0.4N = 0.8N$,
$480 = 1.2N$,
$N = 400$。
【答案】:
400。
7. 将一些数据分成4组,并列出频率分布表,其中第一组的频率是0.23,第二组与第四组的频率之和是0.52,那么第三组的频率是.
答案:
【解析】:
本题主要考察频率分布表中各组频率之和的性质。在频率分布表中,所有组的频率之和必须等于1。
根据题目,第一组的频率是0.23,第二组与第四组的频率之和是0.52。
我们需要找出第三组的频率。
由于所有组的频率之和为1,我们可以通过以下方式计算第三组的频率:
第三组的频率 = 1 - (第一组的频率 + 第二组与第四组的频率之和)
= 1 - (0.23 + 0.52)
= 0.25
【答案】:
第三组的频率是0.25。
本题主要考察频率分布表中各组频率之和的性质。在频率分布表中,所有组的频率之和必须等于1。
根据题目,第一组的频率是0.23,第二组与第四组的频率之和是0.52。
我们需要找出第三组的频率。
由于所有组的频率之和为1,我们可以通过以下方式计算第三组的频率:
第三组的频率 = 1 - (第一组的频率 + 第二组与第四组的频率之和)
= 1 - (0.23 + 0.52)
= 0.25
【答案】:
第三组的频率是0.25。
8. 为了了解某中学八年级两个班男生的身高情况,学校对40名男生的身高(单位:cm)进行了测量,结果如下:
175 168 170 176 167 181 162 173 171 177
179 172 165 167 172 173 166 177 169 181
160 163 166 177 175 174 173 174 171 171
180 170 165 175 165 174 169 163 166 166
(1)制作样本的频数分布表,绘制频数直方图.
(2)根据频数直方图分析,身高在哪个范围内的人数最多?有多少人?40名男生的平均身高在这个范围内吗?
175 168 170 176 167 181 162 173 171 177
179 172 165 167 172 173 166 177 169 181
160 163 166 177 175 174 173 174 171 171
180 170 165 175 165 174 169 163 166 166
(1)制作样本的频数分布表,绘制频数直方图.
(2)根据频数直方图分析,身高在哪个范围内的人数最多?有多少人?40名男生的平均身高在这个范围内吗?
答案:
(1)解:最大值为181,最小值为160,极差=181-160=21,组距取5,分5组。
频数分布表:
|身高范围(cm)|频数|
|----|----|
|160-164|4|
|165-169|10|
|170-174|13|
|175-179|9|
|180-184|4|
(注:频数直方图需根据上述数据绘制,横轴为身高范围,纵轴为频数,每个区间对应矩形高度为相应频数)
(2)解:身高在170-174cm范围内的人数最多,有13人。
计算平均身高:
(175+168+170+176+167+181+162+173+171+177+179+172+165+167+172+173+166+177+169+181+160+163+166+177+175+174+173+174+171+171+180+170+165+175+165+174+169+163+166+166)÷40=6900÷40=172.5cm
172.5cm在170-174cm范围内,故40名男生的平均身高在这个范围内。
(1)解:最大值为181,最小值为160,极差=181-160=21,组距取5,分5组。
频数分布表:
|身高范围(cm)|频数|
|----|----|
|160-164|4|
|165-169|10|
|170-174|13|
|175-179|9|
|180-184|4|
(注:频数直方图需根据上述数据绘制,横轴为身高范围,纵轴为频数,每个区间对应矩形高度为相应频数)
(2)解:身高在170-174cm范围内的人数最多,有13人。
计算平均身高:
(175+168+170+176+167+181+162+173+171+177+179+172+165+167+172+173+166+177+169+181+160+163+166+177+175+174+173+174+171+171+180+170+165+175+165+174+169+163+166+166)÷40=6900÷40=172.5cm
172.5cm在170-174cm范围内,故40名男生的平均身高在这个范围内。
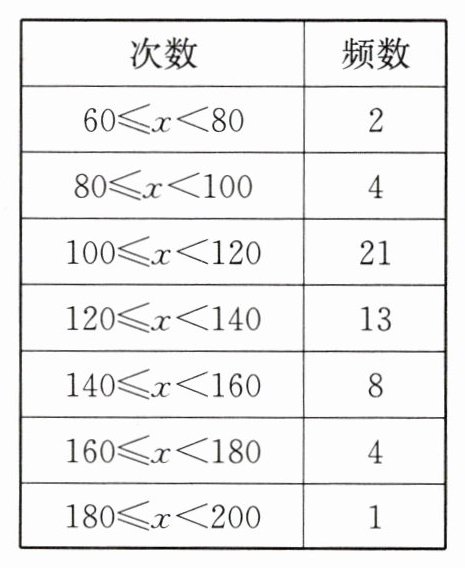
9. 体育委员统计了全班同学60s跳绳的次数,并列出下面的频率分布表:
(1)全班有多少学生?
(2)组距是多少?组数是多少?
(3)跳绳次数x在$100≤x<140$范围内的学生有多少?占全班学生的百分之几?
(4)画出适当的统计图表示上面的信息.
(5)你怎样评价这个班的跳绳成绩?
(1)全班有多少学生?
(2)组距是多少?组数是多少?
(3)跳绳次数x在$100≤x<140$范围内的学生有多少?占全班学生的百分之几?
(4)画出适当的统计图表示上面的信息.
(5)你怎样评价这个班的跳绳成绩?

答案:
1. (1)全班学生人数:
解:全班学生人数为各频数之和,即2 + 4+21 + 13+8 + 4+1=\2 + 4+21 + 13+8 + 4+1\=\53\(人)。2. (2)组距和组数: - 解:组距=后一组下限-前一组下限(如80 - 60=\80 - 60\=\20);
组数是7组$(60\leq x\lt80,$$80\leq x\lt100,$$100\leq x\lt120,$$120\leq x\lt140,$$140\leq x\lt160,$$160\leq x\lt180,$$180\leq x\lt200$共7组)。
$3. (3)100\leq x\lt140$范围内的学生人数及所占百分比:
解:$100\leq x\lt140$范围内的学生人数为21 + 13=\21 + 13\=\34(人); - 占全班学生的百分比为\frac{34}{53}×100\%\approx64.2\%(\frac{34}{53}×100\%=\ \frac{34}{53}×100\%\)。
4. (4)统计图:
解:可画频数分布直方图(以次数为横坐标,频数为纵坐标,每个组距对应一个长方形,长方形的高为该组的频数)。
5. (5)跳绳成绩评价:
解:这个班大部分学生(34人,约占64.2\%)跳绳次数在$100\leq x\lt140$范围内,说明该班学生跳绳成绩整体尚可,但也有少数学生(2 + 4=\2 + 4\=\6人)跳绳次数在100次以下,还有提升空间。
解:全班学生人数为各频数之和,即2 + 4+21 + 13+8 + 4+1=\2 + 4+21 + 13+8 + 4+1\=\53\(人)。2. (2)组距和组数: - 解:组距=后一组下限-前一组下限(如80 - 60=\80 - 60\=\20);
组数是7组$(60\leq x\lt80,$$80\leq x\lt100,$$100\leq x\lt120,$$120\leq x\lt140,$$140\leq x\lt160,$$160\leq x\lt180,$$180\leq x\lt200$共7组)。
$3. (3)100\leq x\lt140$范围内的学生人数及所占百分比:
解:$100\leq x\lt140$范围内的学生人数为21 + 13=\21 + 13\=\34(人); - 占全班学生的百分比为\frac{34}{53}×100\%\approx64.2\%(\frac{34}{53}×100\%=\ \frac{34}{53}×100\%\)。
4. (4)统计图:
解:可画频数分布直方图(以次数为横坐标,频数为纵坐标,每个组距对应一个长方形,长方形的高为该组的频数)。
5. (5)跳绳成绩评价:
解:这个班大部分学生(34人,约占64.2\%)跳绳次数在$100\leq x\lt140$范围内,说明该班学生跳绳成绩整体尚可,但也有少数学生(2 + 4=\2 + 4\=\6人)跳绳次数在100次以下,还有提升空间。
查看更多完整答案,请扫码查看


