6. 五边形的各外角度数之比为$2:3:4:5:6$,这个五边形的最大的内角的度数为
156°
.
答案:
解:设五边形各外角的度数分别为2x,3x,4x,5x,6x。
因为任意多边形的外角和为360°,所以2x+3x+4x+5x+6x=360°。
解得x=12°。
则各外角的度数分别为24°,36°,48°,60°,72°。
因为内角与外角互补,所以最大内角的度数为180°-24°=156°。
答案:156°
因为任意多边形的外角和为360°,所以2x+3x+4x+5x+6x=360°。
解得x=12°。
则各外角的度数分别为24°,36°,48°,60°,72°。
因为内角与外角互补,所以最大内角的度数为180°-24°=156°。
答案:156°
7. 如果一个平行四边形的两邻边的长分别为6和$2\sqrt {7}$,一条对角线的长为8,则这个平行四边形的面积为
12√7
.
答案:
解:设平行四边形ABCD中,AB=6,AD=2√7,对角线AC=8。
在△ABC中,AB=6,BC=AD=2√7,AC=8。
根据余弦定理得:AC²=AB²+BC²-2·AB·BC·cos∠ABC
即8²=6²+(2√7)²-2×6×2√7×cos∠ABC
64=36+28-24√7 cos∠ABC
64=64-24√7 cos∠ABC
24√7 cos∠ABC=0
cos∠ABC=0
∴∠ABC=90°
∴平行四边形ABCD的面积=AB×BC=6×2√7=12√7
答:这个平行四边形的面积为12√7。
在△ABC中,AB=6,BC=AD=2√7,AC=8。
根据余弦定理得:AC²=AB²+BC²-2·AB·BC·cos∠ABC
即8²=6²+(2√7)²-2×6×2√7×cos∠ABC
64=36+28-24√7 cos∠ABC
64=64-24√7 cos∠ABC
24√7 cos∠ABC=0
cos∠ABC=0
∴∠ABC=90°
∴平行四边形ABCD的面积=AB×BC=6×2√7=12√7
答:这个平行四边形的面积为12√7。
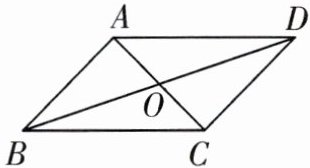
8. 如图,在$□ ABCD$中,对角线AC,BD相交于点O,$AB⊥AC,∠DAC= 45^{\circ },AC= 2$,求BD的长.

答案:
解:
∵四边形ABCD是平行四边形,
∴AD//BC,OA=OC=1/2AC=1,OB=OD=1/2BD。
∵∠DAC=45°,AD//BC,
∴∠ACB=∠DAC=45°。
∵AB⊥AC,
∴∠BAC=90°,△ABC是直角三角形。
在Rt△ABC中,∠ACB=45°,AC=2,
∴AB=AC·tan45°=2×1=2。
在Rt△AOB中,OA=1,AB=2,
由勾股定理得:OB=√(AB²+OA²)=√(2²+1²)=√5。
∴BD=2OB=2√5。
答:BD的长为2√5。
∵四边形ABCD是平行四边形,
∴AD//BC,OA=OC=1/2AC=1,OB=OD=1/2BD。
∵∠DAC=45°,AD//BC,
∴∠ACB=∠DAC=45°。
∵AB⊥AC,
∴∠BAC=90°,△ABC是直角三角形。
在Rt△ABC中,∠ACB=45°,AC=2,
∴AB=AC·tan45°=2×1=2。
在Rt△AOB中,OA=1,AB=2,
由勾股定理得:OB=√(AB²+OA²)=√(2²+1²)=√5。
∴BD=2OB=2√5。
答:BD的长为2√5。
9. 把一个多边形截去一个角后,得到另一个多边形,其内角和为$2160^{\circ }$.画图说明并求原多边形的边数.
答案:
【解析】:
本题主要考查多边形的内角和公式,即$(n-2) × 180^{\circ}$,其中n是多边形的边数。
首先,我们根据给定的内角和$2160^{\circ}$,利用内角和公式反推出截去一个角后的多边形边数。
设新多边形的边数为n,则有$(n-2) × 180^{\circ} = 2160^{\circ}$。
解这个方程,我们可以得到$n=14$。
然后,我们需要考虑截去一个角对多边形边数的影响。
截去一个角,多边形的边数可能增加1(当一个顶点被切去,形成一个新的顶点,边数增加1),可能减少1(当切去的是一个凸角,且切线经过两个相邻的顶点,边数减少1),也可能保持不变(当切去的是一个凸角,但切线只经过一个顶点,边数不变)。
因此,原多边形的边数可能是$14-1=13$,$14+1=15$,或$14$。
【答案】:
原多边形的边数可能为13,14或15。图略。
本题主要考查多边形的内角和公式,即$(n-2) × 180^{\circ}$,其中n是多边形的边数。
首先,我们根据给定的内角和$2160^{\circ}$,利用内角和公式反推出截去一个角后的多边形边数。
设新多边形的边数为n,则有$(n-2) × 180^{\circ} = 2160^{\circ}$。
解这个方程,我们可以得到$n=14$。
然后,我们需要考虑截去一个角对多边形边数的影响。
截去一个角,多边形的边数可能增加1(当一个顶点被切去,形成一个新的顶点,边数增加1),可能减少1(当切去的是一个凸角,且切线经过两个相邻的顶点,边数减少1),也可能保持不变(当切去的是一个凸角,但切线只经过一个顶点,边数不变)。
因此,原多边形的边数可能是$14-1=13$,$14+1=15$,或$14$。
【答案】:
原多边形的边数可能为13,14或15。图略。
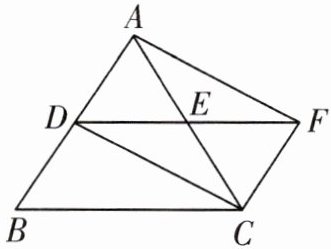
10. 如图,在$\triangle ABC$中,D,E分别是AB,AC的中点,F是DE延长线上的点,且$EF= DE$.
(1)图中的平行四边形有哪几个?请选择其中一个说明理由.
(2)若$\triangle AEF$的面积是3,求四边形BCFD的面积.
(1)图中的平行四边形有哪几个?请选择其中一个说明理由.
(2)若$\triangle AEF$的面积是3,求四边形BCFD的面积.

答案:
【解析】:本题可根据平行四边形的判定定理以及三角形中位线的性质来求解。
(1)判断图中的平行四边形并说明理由
根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形。
已知$D$,$E$分别是$AB$,$AC$的中点,则$DE$是$\triangle ABC$的中位线,根据三角形中位线的性质可知$DE// BC$,且$DE = \frac{1}{2}BC$。
又因为$EF = DE$,所以$DE + EF = DF = 2DE$,即$DF = BC$,且$DF// BC$。
所以四边形$BCFD$是平行四边形,同理四边形$ADFC$也是平行四边形。
(2)求四边形$BCFD$的面积
因为$E$是$AC$的中点,所以$AE = CE$。
已知$EF = DE$,且$\angle AEF = \angle CED$(对顶角相等),根据全等三角形的判定定理($SAS$)可得$\triangle AEF\cong\triangle CED$。
由于$\triangle AEF$的面积是$3$,根据全等三角形的性质可知$\triangle CED$的面积也为$3$。
因为$D$是$AB$的中点,$DE// BC$,所以$DE$是$\triangle ABC$的中位线,根据相似三角形的判定可知$\triangle ADE\sim\triangle ABC$,且相似比为$1:2$。
根据相似三角形的面积比等于相似比的平方,可得$\frac{S_{\triangle ADE}}{S_{\triangle ABC}} = (\frac{1}{2})^2 = \frac{1}{4}$,即$S_{\triangle ABC} = 4S_{\triangle ADE}$。
又因为$S_{\triangle ADE} = S_{\triangle CDE} = 3$,所以$S_{\triangle ABC} = 4×3 = 12$。
那么四边形$BCFD$的面积$S_{BCFD} = S_{\triangle ABC} - S_{\triangle ADE} = 12 - 3 = 9$。
【答案】:
(1)图中的平行四边形有$BCFD$,$ADFC$。以四边形$BCFD$为例,理由:因为$D$,$E$分别是$AB$,$AC$的中点,所以$DE$是$\triangle ABC$的中位线,$DE// BC$,$DE = \frac{1}{2}BC$,又$EF = DE$,所以$DF = BC$,且$DF// BC$,故四边形$BCFD$是平行四边形。
(2)四边形$BCFD$的面积是$9$。
(1)判断图中的平行四边形并说明理由
根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形。
已知$D$,$E$分别是$AB$,$AC$的中点,则$DE$是$\triangle ABC$的中位线,根据三角形中位线的性质可知$DE// BC$,且$DE = \frac{1}{2}BC$。
又因为$EF = DE$,所以$DE + EF = DF = 2DE$,即$DF = BC$,且$DF// BC$。
所以四边形$BCFD$是平行四边形,同理四边形$ADFC$也是平行四边形。
(2)求四边形$BCFD$的面积
因为$E$是$AC$的中点,所以$AE = CE$。
已知$EF = DE$,且$\angle AEF = \angle CED$(对顶角相等),根据全等三角形的判定定理($SAS$)可得$\triangle AEF\cong\triangle CED$。
由于$\triangle AEF$的面积是$3$,根据全等三角形的性质可知$\triangle CED$的面积也为$3$。
因为$D$是$AB$的中点,$DE// BC$,所以$DE$是$\triangle ABC$的中位线,根据相似三角形的判定可知$\triangle ADE\sim\triangle ABC$,且相似比为$1:2$。
根据相似三角形的面积比等于相似比的平方,可得$\frac{S_{\triangle ADE}}{S_{\triangle ABC}} = (\frac{1}{2})^2 = \frac{1}{4}$,即$S_{\triangle ABC} = 4S_{\triangle ADE}$。
又因为$S_{\triangle ADE} = S_{\triangle CDE} = 3$,所以$S_{\triangle ABC} = 4×3 = 12$。
那么四边形$BCFD$的面积$S_{BCFD} = S_{\triangle ABC} - S_{\triangle ADE} = 12 - 3 = 9$。
【答案】:
(1)图中的平行四边形有$BCFD$,$ADFC$。以四边形$BCFD$为例,理由:因为$D$,$E$分别是$AB$,$AC$的中点,所以$DE$是$\triangle ABC$的中位线,$DE// BC$,$DE = \frac{1}{2}BC$,又$EF = DE$,所以$DF = BC$,且$DF// BC$,故四边形$BCFD$是平行四边形。
(2)四边形$BCFD$的面积是$9$。
查看更多完整答案,请扫码查看


