4. 如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点$A,B的坐标分别为(-1,0),(0,\sqrt{3})$.现将该三角板向右平移,使点$A与点O$重合,得到$\triangle OCB'$,则点$B的对应点B'$的坐标是 (

A.$(1,0)$
B.$(\sqrt{3},\sqrt{3})$
C.$(1,\sqrt{3})$
D.$(-1,\sqrt{3})$
C
)
A.$(1,0)$
B.$(\sqrt{3},\sqrt{3})$
C.$(1,\sqrt{3})$
D.$(-1,\sqrt{3})$
答案:
【解析】:本题可根据点在平面直角坐标系中平移的规律来求解点$B$的对应点$B'$的坐标。
在平面直角坐标系中,点的平移规律是:左右平移时,纵坐标不变,向右移动几个单位横坐标就加上几,向左移动几个单位横坐标就减去几;上下平移时,横坐标不变,向上移动几个单位纵坐标就加上几,向下移动几个单位纵坐标就减去几。
已知点$A$的坐标为$(-1,0)$,将三角板向右平移使点$A$与点$O$重合,点$A$的横坐标从$-1$变为$0$,说明点$A$向右平移了$0 - (-1)=1$个单位。
因为三角板是整体平移,所以点$B$也向右平移了$1$个单位。
点$B$的坐标为$(0,\sqrt{3})$,根据上述平移规律,纵坐标不变,横坐标加上$1$,即$0 + 1 = 1$,所以点$B$的对应点$B'$的坐标是$(1,\sqrt{3})$。
【答案】:C。
在平面直角坐标系中,点的平移规律是:左右平移时,纵坐标不变,向右移动几个单位横坐标就加上几,向左移动几个单位横坐标就减去几;上下平移时,横坐标不变,向上移动几个单位纵坐标就加上几,向下移动几个单位纵坐标就减去几。
已知点$A$的坐标为$(-1,0)$,将三角板向右平移使点$A$与点$O$重合,点$A$的横坐标从$-1$变为$0$,说明点$A$向右平移了$0 - (-1)=1$个单位。
因为三角板是整体平移,所以点$B$也向右平移了$1$个单位。
点$B$的坐标为$(0,\sqrt{3})$,根据上述平移规律,纵坐标不变,横坐标加上$1$,即$0 + 1 = 1$,所以点$B$的对应点$B'$的坐标是$(1,\sqrt{3})$。
【答案】:C。
5. 如图,在平面直角坐标系中,四边形$ABCD的顶点A,B,C,D的坐标分别是(0,0),(5,0),(7,4),(2,4)$,则这个四边形的面积是 (
A.6
B.8
C.20
D.12
C
)A.6
B.8
C.20
D.12
答案:
【解析】:
由题意,点$A$、$B$的坐标分别为$A(0,0)$,$B(5,0)$,所以$AB = 5 - 0 = 5$。
点$C$、$D$的坐标分别为$C(7,4)$,$D(2,4)$,所以$CD$的长度为$7 - 2 = 5$,且$CD$到$x$轴的距离(即$y$坐标的差)为$4$。
因为$AB$和$CD$平行且长度相等(都等于$5$),且它们到$x$轴的距离都为$4$,所以四边形$ABCD$是一个平行四边形。
平行四边形的高就是$CD$(或$AB$)到$x$轴的距离,即$4$。
根据平行四边形的面积公式:面积 = 底 × 高,所以四边形$ABCD$的面积为:$5 × 4 = 20$。
【答案】:C
由题意,点$A$、$B$的坐标分别为$A(0,0)$,$B(5,0)$,所以$AB = 5 - 0 = 5$。
点$C$、$D$的坐标分别为$C(7,4)$,$D(2,4)$,所以$CD$的长度为$7 - 2 = 5$,且$CD$到$x$轴的距离(即$y$坐标的差)为$4$。
因为$AB$和$CD$平行且长度相等(都等于$5$),且它们到$x$轴的距离都为$4$,所以四边形$ABCD$是一个平行四边形。
平行四边形的高就是$CD$(或$AB$)到$x$轴的距离,即$4$。
根据平行四边形的面积公式:面积 = 底 × 高,所以四边形$ABCD$的面积为:$5 × 4 = 20$。
【答案】:C
6. 如图,小鱼的鱼身$ABCD$为菱形.已知鱼身长$BD= 8,AB= 5$,以$BD所在直线为x$轴,以$AC所在直线为y$轴,建立平面直角坐标系,则点$C$的坐标为
$(0, - 3)$
.
答案:
【解析】:
本题题干可知鱼身$ABCD$为菱形,这就说明$AC$和$BD$互相垂直且平分,我们可以先求出$AC$长度的一半,即$AO$的长度,再求出$CO$的长度,最后就可以得出点$C$的坐标。
因为四边形$ABCD$是菱形,$BD$在$x$轴上,$AC$在$y$轴上,$BD = 8$,所以$BO=\frac{1}{2}BD = 4$。
在$Rt\bigtriangleup ABO$中,$AB = 5$,$BO = 4$,根据勾股定理$a^2 +b^2 =c^2$(其中$c$为斜边,$a$、$b$为两直角边),可得:
$AO=\sqrt{AB^{2}-BO^{2}}=\sqrt{5^{2}-4^{2}}=\sqrt{25 - 16}=\sqrt{9}=3$。
因为菱形的对角线互相平分,$AC$与$BD$互相垂直平分,$AO = 3$,所以$CO = AO = 3$。
又因为点$C$在$y$轴负半轴上,所以点$C$的坐标为$(0, - 3)$。
【答案】:$(0, - 3)$。
本题题干可知鱼身$ABCD$为菱形,这就说明$AC$和$BD$互相垂直且平分,我们可以先求出$AC$长度的一半,即$AO$的长度,再求出$CO$的长度,最后就可以得出点$C$的坐标。
因为四边形$ABCD$是菱形,$BD$在$x$轴上,$AC$在$y$轴上,$BD = 8$,所以$BO=\frac{1}{2}BD = 4$。
在$Rt\bigtriangleup ABO$中,$AB = 5$,$BO = 4$,根据勾股定理$a^2 +b^2 =c^2$(其中$c$为斜边,$a$、$b$为两直角边),可得:
$AO=\sqrt{AB^{2}-BO^{2}}=\sqrt{5^{2}-4^{2}}=\sqrt{25 - 16}=\sqrt{9}=3$。
因为菱形的对角线互相平分,$AC$与$BD$互相垂直平分,$AO = 3$,所以$CO = AO = 3$。
又因为点$C$在$y$轴负半轴上,所以点$C$的坐标为$(0, - 3)$。
【答案】:$(0, - 3)$。
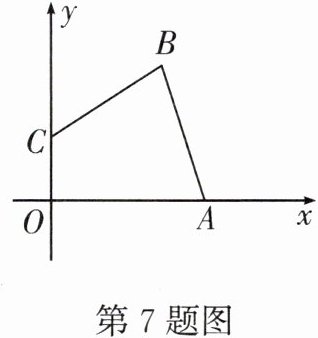
7. 如图,在平面直角坐标系中,$A,B,C三点的坐标分别为(4,0),(3,4),(0,2)$,则四边形$ABCO$的面积为______.

11
答案:
解:过点B作BD⊥x轴于点D,
∵B(3,4),
∴D(3,0),BD=4,
∵A(4,0),O(0,0),C(0,2),
∴OA=4,OD=3,AD=OA-OD=1,OC=2,
S四边形ABCO=S梯形OCDB+S△ABD,
S梯形OCDB=$\frac{1}{2}$×(OC+BD)×OD=$\frac{1}{2}$×(2+4)×3=9,
S△ABD=$\frac{1}{2}$×AD×BD=$\frac{1}{2}$×1×4=2,
∴S四边形ABCO=9+2=11.
11
∵B(3,4),
∴D(3,0),BD=4,
∵A(4,0),O(0,0),C(0,2),
∴OA=4,OD=3,AD=OA-OD=1,OC=2,
S四边形ABCO=S梯形OCDB+S△ABD,
S梯形OCDB=$\frac{1}{2}$×(OC+BD)×OD=$\frac{1}{2}$×(2+4)×3=9,
S△ABD=$\frac{1}{2}$×AD×BD=$\frac{1}{2}$×1×4=2,
∴S四边形ABCO=9+2=11.
11
8. 已知点$M的坐标可表示为(3a-8,a-1)$,请分别根据下列条件求出点$M$的坐标.
(1)点$M在y$轴上.
(2)点$N的坐标为(3,-6)$,直线$MN// x$轴.
(1)点$M在y$轴上.
(2)点$N的坐标为(3,-6)$,直线$MN// x$轴.
答案:
【解析】:
本题主要考察平面直角坐标系中,点的坐标与所在位置的关系,以及平行于坐标轴的直线上的点的坐标特征。
(1) 对于点$M$在$y$轴上的情况,需要利用$y$轴上点的横坐标都为$0$的性质。因此,将$3a-8=0$,解这个方程得到$a$的值,再代入$a-1$求出$y$坐标。
(2) 对于直线$MN$平行于$x$轴的情况,需要利用平行于$x$轴的直线上的点的纵坐标都相等的性质。因此,将$a-1=-6$,解这个方程得到$a$的值,再代入$3a-8$求出$x$坐标。
【答案】:
(1) 解:
由于点$M$在$y$轴上,根据$y$轴上点的横坐标为$0$的性质,有:
$3a - 8 = 0$
解得:
$a = \frac{8}{3}$
将$a=\frac{8}{3}$代入$a-1$得:
$a - 1 = \frac{8}{3} - 1 = \frac{5}{3}$
因此,点$M$的坐标为$(0, \frac{5}{3})$。
(2) 解:
由于直线$MN$平行于$x$轴,根据平行于$x$轴的直线上的点的纵坐标相等的性质,有:
$a - 1 = -6$
解得:
$a = -5$
将$a=-5$代入$3a-8$得:
$3a - 8 = 3 × (-5) - 8 = -15 - 8 = -23$
因此,点$M$的坐标为$(-23, -6)$。
本题主要考察平面直角坐标系中,点的坐标与所在位置的关系,以及平行于坐标轴的直线上的点的坐标特征。
(1) 对于点$M$在$y$轴上的情况,需要利用$y$轴上点的横坐标都为$0$的性质。因此,将$3a-8=0$,解这个方程得到$a$的值,再代入$a-1$求出$y$坐标。
(2) 对于直线$MN$平行于$x$轴的情况,需要利用平行于$x$轴的直线上的点的纵坐标都相等的性质。因此,将$a-1=-6$,解这个方程得到$a$的值,再代入$3a-8$求出$x$坐标。
【答案】:
(1) 解:
由于点$M$在$y$轴上,根据$y$轴上点的横坐标为$0$的性质,有:
$3a - 8 = 0$
解得:
$a = \frac{8}{3}$
将$a=\frac{8}{3}$代入$a-1$得:
$a - 1 = \frac{8}{3} - 1 = \frac{5}{3}$
因此,点$M$的坐标为$(0, \frac{5}{3})$。
(2) 解:
由于直线$MN$平行于$x$轴,根据平行于$x$轴的直线上的点的纵坐标相等的性质,有:
$a - 1 = -6$
解得:
$a = -5$
将$a=-5$代入$3a-8$得:
$3a - 8 = 3 × (-5) - 8 = -15 - 8 = -23$
因此,点$M$的坐标为$(-23, -6)$。
查看更多完整答案,请扫码查看


