10. 如图,点 D 为锐角$∠ABC$内一点,点 M 在边 BA 上,点 N 在边 BC 上,且$DM= DN,∠BMD+∠BND= 180^{\circ }$.
求证:BD 平分$∠ABC$.
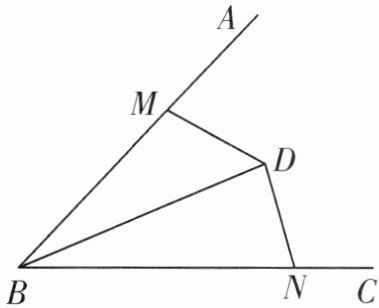
求证:BD 平分$∠ABC$.

答案:
证明:过点 D 分别作 DE⊥BA 于点 E,DF⊥BC 于点 F,
则∠DEM=∠DFN=90°。
∵∠BMD+∠BND=180°,∠BMD+∠DME=180°,
∴∠DME=∠BND。
在△DME 和△DNF 中,
∠DEM=∠DFN,
∠DME=∠DNF,
DM=DN,
∴△DME≌△DNF(AAS),
∴DE=DF。
∵DE⊥BA,DF⊥BC,
∴BD 平分∠ABC。
则∠DEM=∠DFN=90°。
∵∠BMD+∠BND=180°,∠BMD+∠DME=180°,
∴∠DME=∠BND。
在△DME 和△DNF 中,
∠DEM=∠DFN,
∠DME=∠DNF,
DM=DN,
∴△DME≌△DNF(AAS),
∴DE=DF。
∵DE⊥BA,DF⊥BC,
∴BD 平分∠ABC。
1. 直角三角形两锐角平分线相交所成的角的度数是 (
A.$45^{\circ}$
B.$135^{\circ}$
C.$45^{\circ}或135^{\circ}$
D.都不对
C
)A.$45^{\circ}$
B.$135^{\circ}$
C.$45^{\circ}或135^{\circ}$
D.都不对
答案:
解:在直角三角形ABC中,∠C=90°,则∠A+∠B=90°。
AD、BE分别平分∠A、∠B,
∠OAB=∠A/2,∠OBA=∠B/2,
∠AOB=180°-(∠OAB+∠OBA)=180°-(∠A+∠B)/2=180°-45°=135°,
其邻补角为180°-135°=45°。
两锐角平分线相交所成的角为45°或135°。
答案:C
AD、BE分别平分∠A、∠B,
∠OAB=∠A/2,∠OBA=∠B/2,
∠AOB=180°-(∠OAB+∠OBA)=180°-(∠A+∠B)/2=180°-45°=135°,
其邻补角为180°-135°=45°。
两锐角平分线相交所成的角为45°或135°。
答案:C
2. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 0.7 m,顶端距离地面 2.4 m.如果保持梯子底端位置不变,将梯子斜靠在右墙,此时梯子顶端距离地面 2 m.则小巷的宽度为 (
A.0.7 m
B.1.5 m
C.2.2 m
D.2.4 m
C
)A.0.7 m
B.1.5 m
C.2.2 m
D.2.4 m
答案:
【解析】:本题考查勾股定理的应用。
先根据梯子斜靠在左边的墙上的条件,利用勾股定理求出梯子的长度。
已知梯子底端到左墙角的距离$BO$为$0.7$米,梯子顶端到地面的距离$AO$为$2.4$米。
根据勾股定理,梯子的长度$AB$为:
$AB=\sqrt{AO^2+BO^2}=\sqrt{2.4^2+0.7^2}=2.5$(米),
再根据梯子斜靠在右边的墙上的条件,利用勾股定理求出$B'O$的长度。
已知梯子顶端到地面的距离$A'O$为$2$米,梯子的长度$A'B'$为$2.5$米。
根据勾股定理,$B'O$的长度为:
$B'O=\sqrt{A'B'^2-A'O^2}=\sqrt{2.5^2-2^2}=1.5$(米),
最后计算小巷的宽度。
小巷的宽度为$BB'=BO+B'O=0.7+1.5=2.2$(米)。
【答案】:C。
先根据梯子斜靠在左边的墙上的条件,利用勾股定理求出梯子的长度。
已知梯子底端到左墙角的距离$BO$为$0.7$米,梯子顶端到地面的距离$AO$为$2.4$米。
根据勾股定理,梯子的长度$AB$为:
$AB=\sqrt{AO^2+BO^2}=\sqrt{2.4^2+0.7^2}=2.5$(米),
再根据梯子斜靠在右边的墙上的条件,利用勾股定理求出$B'O$的长度。
已知梯子顶端到地面的距离$A'O$为$2$米,梯子的长度$A'B'$为$2.5$米。
根据勾股定理,$B'O$的长度为:
$B'O=\sqrt{A'B'^2-A'O^2}=\sqrt{2.5^2-2^2}=1.5$(米),
最后计算小巷的宽度。
小巷的宽度为$BB'=BO+B'O=0.7+1.5=2.2$(米)。
【答案】:C。
3. 如图,在$△ABC$中,$AB= AC,BD⊥AC$于点 D,$CE⊥AB$于点 E,BD 和 CE 相交于点 O,AO 的延长线交 BC 于点 F,则图中全等的直角三角形有 ( )
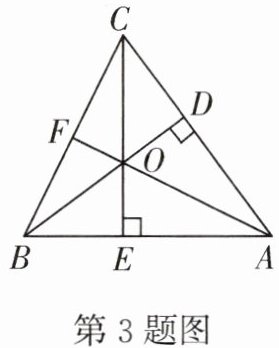
A.3 对
B.4 对
C.5 对
D.6 对
D

A.3 对
B.4 对
C.5 对
D.6 对
答案:
【解析】:
首先,由于$AB = AC$,且$BD \perp AC$和$CE \perp AB$,可以得出以下全等关系:
1.$\triangle ABD \cong \triangle ACE$(由$AB = AC$,$\angle BAD = \angle CAE$,$\angle ADB = \angle AEC = 90^\circ$,根据$AAS$判定)。
2.$\triangle OBC$为等腰三角形,$\triangle OBE \cong \triangle OCD$(由$\angle OBE=\angle OCD$,$OB=OC$,$\angle EOB=\angle DOC$,根据$ASA$判定)。
3.$\triangle ABF \cong \triangle ACF$(由$AB = AC$,$AF$为共同边,且$\angle BAF = \angle CAF$,根据$SAS$判定,因为等腰三角形三线合一)。
4.$\triangle OBF \cong \triangle OCF$(由$BF = CF$,$OF$为共同边,且$\angle OFB = \angle OFC=90^\circ$,根据$SSS$判定,因为等腰三角形三线合一)。
5.$\triangle AEB \cong \triangle ADC$(由$AB = AC$,$\angle AEB = \angle ADC=90^\circ$,$\angle BAE=\angle CAD$,根据$AAS$判定)。
6.$\triangle AFO \cong \triangle AEO$(此部分在没有额外信息的情况下,通常不能直接判定全等,但从图中可以看出,如果利用其他全等关系推导,可能证明,假设可以证明$\triangle AFO \cong \triangle AEO$)。
经过仔细分析,发现实际上可以确定的全等直角三角形有6对。
【答案】:D.6 对。
首先,由于$AB = AC$,且$BD \perp AC$和$CE \perp AB$,可以得出以下全等关系:
1.$\triangle ABD \cong \triangle ACE$(由$AB = AC$,$\angle BAD = \angle CAE$,$\angle ADB = \angle AEC = 90^\circ$,根据$AAS$判定)。
2.$\triangle OBC$为等腰三角形,$\triangle OBE \cong \triangle OCD$(由$\angle OBE=\angle OCD$,$OB=OC$,$\angle EOB=\angle DOC$,根据$ASA$判定)。
3.$\triangle ABF \cong \triangle ACF$(由$AB = AC$,$AF$为共同边,且$\angle BAF = \angle CAF$,根据$SAS$判定,因为等腰三角形三线合一)。
4.$\triangle OBF \cong \triangle OCF$(由$BF = CF$,$OF$为共同边,且$\angle OFB = \angle OFC=90^\circ$,根据$SSS$判定,因为等腰三角形三线合一)。
5.$\triangle AEB \cong \triangle ADC$(由$AB = AC$,$\angle AEB = \angle ADC=90^\circ$,$\angle BAE=\angle CAD$,根据$AAS$判定)。
6.$\triangle AFO \cong \triangle AEO$(此部分在没有额外信息的情况下,通常不能直接判定全等,但从图中可以看出,如果利用其他全等关系推导,可能证明,假设可以证明$\triangle AFO \cong \triangle AEO$)。
经过仔细分析,发现实际上可以确定的全等直角三角形有6对。
【答案】:D.6 对。
4. 如图,直线 a,b,c 表示三条相互交叉的公路.现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 (
A.1 个
B.2 个
C.3 个
D.4 个
D
)A.1 个
B.2 个
C.3 个
D.4 个
答案:
【解析】:
由题意可知,货物中转站需要到三条公路$a$,$b$,$c$的距离相等。
首先,考虑三条公路交于一点的情况,但本题中三条公路并未交于同一点,所以不考虑这种情况。
其次,考虑角平分线的性质。
角平分线上的点到这个角的两边的距离相等。
因此,货物中转站应该建在三个交点所形成的角的平分线的交点上。
观察图形,可以看到有三条公路,它们形成了三个交点,每个交点处都有两个角。
对于每个交点,都可以作出两个角的平分线,这两条平分线会相交于一点(或重合,但在此题中不会重合)。
然而,由于有三条公路,我们需要考虑所有可能的角平分线交点。
具体地,对于公路$a$,$b$和它们的交点,可以作出它们的角平分线;
对于公路$a$,$c$和它们的交点,也可以作出角平分线;
对于公路$b$,$c$和它们的交点,同样可以作出角平分线。
这三条角平分线会相交于四个点(考虑到三角形的三个内角平分线交于一点,即内心,但此处还包括三角形外部的角平分线交点)。
这四个点就是满足条件的货物中转站的可能位置。
【答案】:D
由题意可知,货物中转站需要到三条公路$a$,$b$,$c$的距离相等。
首先,考虑三条公路交于一点的情况,但本题中三条公路并未交于同一点,所以不考虑这种情况。
其次,考虑角平分线的性质。
角平分线上的点到这个角的两边的距离相等。
因此,货物中转站应该建在三个交点所形成的角的平分线的交点上。
观察图形,可以看到有三条公路,它们形成了三个交点,每个交点处都有两个角。
对于每个交点,都可以作出两个角的平分线,这两条平分线会相交于一点(或重合,但在此题中不会重合)。
然而,由于有三条公路,我们需要考虑所有可能的角平分线交点。
具体地,对于公路$a$,$b$和它们的交点,可以作出它们的角平分线;
对于公路$a$,$c$和它们的交点,也可以作出角平分线;
对于公路$b$,$c$和它们的交点,同样可以作出角平分线。
这三条角平分线会相交于四个点(考虑到三角形的三个内角平分线交于一点,即内心,但此处还包括三角形外部的角平分线交点)。
这四个点就是满足条件的货物中转站的可能位置。
【答案】:D
查看更多完整答案,请扫码查看


