第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 已知线段 $ AB = 3 \text{ cm} $,延长线段 $ AB $ 到 $ C $,使 $ BC = 4 \text{ cm} $,则线段 $ AC $ 的长为 (
A.$ 1 \text{ cm} $
B.$ 6 \text{ cm} $
C.$ 7 \text{ cm} $
D.$ 8 \text{ cm} $
C
)A.$ 1 \text{ cm} $
B.$ 6 \text{ cm} $
C.$ 7 \text{ cm} $
D.$ 8 \text{ cm} $
答案:
C 由线段的和差得,AC=AB+BC=3+4=7(cm).
(1) $ AD = $
(2) $ AB = AD - $
(3) $ AC = BC + $
(4) $ BD - CD + AB = $
AB
$ + BC + $CD
$ = AB + $BD
$ = CD + $AC
;(2) $ AB = AD - $
BD
;(3) $ AC = BC + $
AB
$ = AD - $CD
;(4) $ BD - CD + AB = $
AC
.
答案:
(1)AB CD BD AC;
(2)BD;
(3)AB CD;
(4)AC
(1)AB CD BD AC;
(2)BD;
(3)AB CD;
(4)AC
3 [2025 唐山滦州期中] 如图,画射线 $ PQ $,在射线 $ PQ $ 上依次截取 $ PA = AB = 2 $,在线段 $ PB $ 上截取 $ BC = 3 $,则 $ PC $ 的长为______.
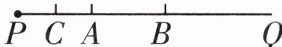
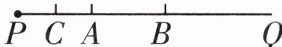
1
答案:
1 因为PA=AB=2,所以PB=PA+AB=4.因为BC=3,所以PC=PB-BC=4-3=1.
4 教材 P165 例 1 变式 一题多解 如图,已知线段 $ a $,$ b $,用圆规和无刻度的直尺作一条线段 $ AB $,使 $ AB = 2b - 2a $.
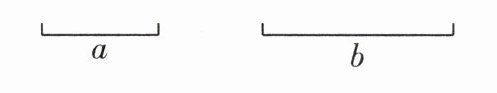
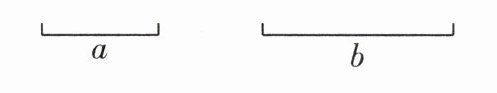
答案:
解:通解 如图1,在直线上作线段AC=b,在线段AC的延长线上作线段CD=b,则线段AD=2b.在线段AD上作线段DE=a,再作线段EB=a,则线段DB=2a,AB=AD-DB=2b-2a.

另解 如图2,在直线上作线段AC=b,在线段AC上作线段CD=a,则线段AD=b-a,最后在线段AD的延长线上作线段DB=AD=b-a,所以线段AB=b-a+b-a=2b-2a.

解:通解 如图1,在直线上作线段AC=b,在线段AC的延长线上作线段CD=b,则线段AD=2b.在线段AD上作线段DE=a,再作线段EB=a,则线段DB=2a,AB=AD-DB=2b-2a.

另解 如图2,在直线上作线段AC=b,在线段AC上作线段CD=a,则线段AD=b-a,最后在线段AD的延长线上作线段DB=AD=b-a,所以线段AB=b-a+b-a=2b-2a.

5 [2025 莆田荔城区期末] 点 $ C $ 在线段 $ AB $ 上,下列条件中,不能确定点 $ C $ 是线段 $ AB $ 的中点的是 (
A.$ AC = BC $
B.$ AC + BC = AB $
C.$ AB = 2AC $
D.$ BC = \frac{1}{2}AB $
B
)A.$ AC = BC $
B.$ AC + BC = AB $
C.$ AB = 2AC $
D.$ BC = \frac{1}{2}AB $
答案:
B 易知当点C在线段AB上时,选项A,C,D都可以确定点C是线段AB的中点.点C在线段AB上任意位置都满足AC+BC=AB,所以选项B不能确定点C是线段AB的中点.
6 [2025 上海黄浦区期末] 如图,$ C $ 是线段 $ AD $ 的中点,如果 $ AC = 1.5 \text{ cm} $,$ BC = 2.3 \text{ cm} $,那么 $ BD = $
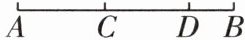
变式 [2025 开封通许期末] 如图,长度为 $ 12 \text{ cm} $ 的线段 $ AB $ 的中点为 $ M $,$ C $ 为线段 $ MB $ 上一点,且 $ MC:CB = 1:2 $,则线段 $ AC $ 的长度为
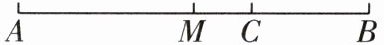
0.8
$ \text{cm} $.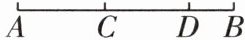
变式 [2025 开封通许期末] 如图,长度为 $ 12 \text{ cm} $ 的线段 $ AB $ 的中点为 $ M $,$ C $ 为线段 $ MB $ 上一点,且 $ MC:CB = 1:2 $,则线段 $ AC $ 的长度为
8
$ \text{cm} $.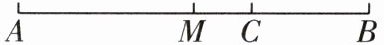
答案:
0.8 因为点C是线段AD的中点,AC=1.5cm,所以CD=AC=1.5cm.因为BC=2.3cm,所以BD=BC-CD=0.8cm.
变式8 因为长度为12cm的线段AB的中点为M,所以AM=BM=6cm,因为MC:CB=1:2,所以MC=$\frac{1}{3}$BM=2cm,所以AC=AM+MC=6+2=8(cm).
变式8 因为长度为12cm的线段AB的中点为M,所以AM=BM=6cm,因为MC:CB=1:2,所以MC=$\frac{1}{3}$BM=2cm,所以AC=AM+MC=6+2=8(cm).
7 如图,线段 $ AB = 10 \text{ cm} $,$ C $ 是线段 $ AB $ 上一点,$ AC = 4 \text{ cm} $,$ M $ 是 $ AB $ 的中点,$ N $ 是 $ AC $ 的中点.
求:(1) 线段 $ CM $ 的长;
(2) 线段 $ MN $ 的长.
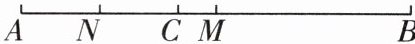
求:(1) 线段 $ CM $ 的长;
(2) 线段 $ MN $ 的长.
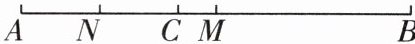
答案:
7 解题思路:
(1)根据M是AB的中点,求出AM的长度,再利用CM=AM-AC求得线段CM的长度;
(2)根据N是AC的中点求出NC的长度,再利用MN=CM+NC即可求出MN的长度.
解:
(1)因为AB=10cm,M是AB的中点,所以AM=5cm.因为AC=4cm,所以CM=AM-AC=5-4=1(cm).
(2)因为N是AC的中点,所以NC=$\frac{1}{2}$AC=2cm,所以MN=NC+CM=2+1=3(cm).
(1)根据M是AB的中点,求出AM的长度,再利用CM=AM-AC求得线段CM的长度;
(2)根据N是AC的中点求出NC的长度,再利用MN=CM+NC即可求出MN的长度.
解:
(1)因为AB=10cm,M是AB的中点,所以AM=5cm.因为AC=4cm,所以CM=AM-AC=5-4=1(cm).
(2)因为N是AC的中点,所以NC=$\frac{1}{2}$AC=2cm,所以MN=NC+CM=2+1=3(cm).
8 [2025 济宁兖州区期末节选] 如图,线段 $ AC $ 上依次有 $ D $,$ B $,$ E $ 三点,$ AD = \frac{1}{2}DB $,$ E $ 是 $ BC $ 的中点,$ BE = \frac{1}{5}AC = 2 $.
(1) 求线段 $ AB $ 的长;
(2) 求线段 $ DE $ 的长.

(1) 求线段 $ AB $ 的长;
(2) 求线段 $ DE $ 的长.

答案:
8 解:
(1)因为BE=$\frac{1}{5}$AC=2,所以AC=5BE=5×2=10.因为E是BC的中点,所以BC=2BE=2×2=4,所以AB=AC-BC=10-4=6.
(2)因为AD=$\frac{1}{2}$DB,所以DB=$\frac{2}{3}$AB=$\frac{2}{3}$×6=4,所以DE=DB+BE=4+2=6.
(1)因为BE=$\frac{1}{5}$AC=2,所以AC=5BE=5×2=10.因为E是BC的中点,所以BC=2BE=2×2=4,所以AB=AC-BC=10-4=6.
(2)因为AD=$\frac{1}{2}$DB,所以DB=$\frac{2}{3}$AB=$\frac{2}{3}$×6=4,所以DE=DB+BE=4+2=6.
查看更多完整答案,请扫码查看


