《2025年一遍过七年级数学上册人教版》

1 [2024贵州中考]小红学习了等式的性质后,在甲、乙两台天平的左右两边分别放入“■”“●”“▲”三种物体,如图所示,天平都保持平衡。若设“■”与“●”的质量分别为x,y,则下列关系式正确的是(C)

A.$x = y$
B.$x = 2y$
C.$x = 4y$
D.$x = 5y$

答案： C 设“▲”的质量为a,由甲图可得x+y=y+2a,即x=2a,由乙图可得x+a=x+2y,即a=2y,所以x=4y.

我国古代问题：以绳测井,若将绳三折测之,绳多四尺；若将绳四折测之,绳多一尺。绳长、井深各几何？这段话的意思是用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺。绳长、井深各几尺？若设绳长为x尺,则可列方程为(A)
A.$\frac{1}{3}x - 4 = \frac{1}{4}x - 1$
B.$\frac{1}{3}x + 4 = \frac{1}{4}x - 1$
C.$\frac{1}{3}x - 4 = \frac{1}{4}x + 1$
D.$\frac{1}{3}x + 4 = \frac{1}{4}x + 1$

答案： A

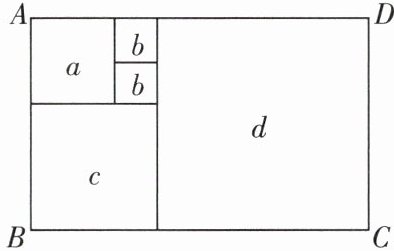
3 [2022乐山中考]如果一个长方形内部能用一些正方形铺满,既不重叠,又无缝隙,就称它为“优美长方形”。如图所示,“优美长方形”ABCD的周长为26,则正方形d的边长为______。

5

答案： 5 设正方形b的边长为x,则正方形a的边长为2x,正方形c的边长为3x,正方形d的边长为5x.根据题意得(3x+5x+5x)×2=26,解得x=1,则5x=5×1=5,即正方形d的边长为5.

为庆祝中国改革开放46周年,某中学举办了一场精彩纷呈的庆祝活动,现场参与者均为在校中学生,其中有一个活动项目是“选数字猜出生年份”,该活动项目主持人要求参与者从1,2,3,4,5,6,7,8,9这九个数字中任取一个数字,先乘10,再加上4.6,将此时的运算结果再乘10,然后加上1978,最后减去参与者的出生年份(注：出生年份是一个四位数,比如2010年对应的四位数是2010),得到最终的运算结果。只要参与者报出最终的运算结果,主持人立马就知道参与者的出生年份。若某位参与者报出的最终的运算结果是915,则这位参与者的出生年份是______2009。

答案： 2009 设这位参与者的出生年份为x,选取的数字为m,则(10m+4.6)×10+1978-x=915,所以x=1109+100m,因为此时中学生的出生时间应该在2000年后,所以m=9,所以x=2009.故这位参与者的出生年份是2009.

5 [2024北京中考]为防治污染,保护和改善生态环境,自2023年7月1日起,我国全面实施汽车国六排放标准6b阶段(以下简称“标准”)。对某型号汽车,“标准”要求A类物质排放量不超过35mg/km,A,B两类物质排放量之和不超过50mg/km。已知该型号某汽车的A,B两类物质排放量之和原为92mg/km。经过一次技术改进,该汽车的A类物质排放量降低了50%,B类物质排放量降低了75%,A,B两类物质排放量之和为40mg/km,判断这次技术改进后该汽车的A类物质排放量是否符合“标准”,并说明理由。

答案： 解:这次技术改进后该汽车的A类物质排放量符合“标准”.理由如下:
设技术改进后该汽车的A类物质排放量为x mg/km,则B类物质排放量为(40-x)mg/km,
由题意,得x/(1-50%)+(40-x)/(1-75%)=92,解得x=34.
因为34＜35,所以这次技术改进后该汽车的A类物质排放量符合“标准”.

6 [跨学科·物理][2023南京中考]如图,某校的饮水机有温水、开水两个按钮,温水和开水共用一个出水口。温水的温度为30℃,流速为20mL/s；开水的温度为100℃,流速为15mL/s。某学生先接了一会儿温水,又接了一会儿开水,得到一杯280mL温度为60℃的水(不计热损失),求该学生分别接温水和开水的时间。
物理常识
开水和温水混合时会发生热传递,开水放出的热量等于温水吸收的热量,可以转化为开水的体积×开水降低的温度= 温水的体积×温水升高的温度。

答案： 解:设该学生接温水的时间为x s.
根据题意,得20x×(60-30)=(280-20x)×(100-60),解得x=8,所以20x=160,因为280-160=120(mL),所以120÷15=8(s),所以该学生接温水的时间为8s,接开水的时间为8s.