第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 已知$|x|= 5,|y|= 4.$
(1)若$xy<0$,则$x+y$的值为
(2)若$|x+y|= x+y$,则$xy$的值为
(1)若$xy<0$,则$x+y$的值为
-1或1
;(2)若$|x+y|= x+y$,则$xy$的值为
-20或20
.
答案:
1
(1)-1或1;
(2)-20或20 因为|x|=5,|y|=4,所以x=±5,y=±4.
(1)因为xy<0(x,y异号),所以x=5,y=-4或x=-5,y=4,所以x+y=-1或1.
(2)因为|x+y|=x+y,所以x+y≥0,所以x=5,y=-4或4,所以xy=-20或20.
(1)-1或1;
(2)-20或20 因为|x|=5,|y|=4,所以x=±5,y=±4.
(1)因为xy<0(x,y异号),所以x=5,y=-4或x=-5,y=4,所以x+y=-1或1.
(2)因为|x+y|=x+y,所以x+y≥0,所以x=5,y=-4或4,所以xy=-20或20.
2 若$ab>0$,化简:$\frac {|a|}{a}+\frac {|b|}{b}-\frac {|ab|}{ab}=$
1或-3
.
答案:
2 1或-3 解题思路:化简含绝对值的式子,先确定绝对值符号内式子的正负,再去绝对值符号.因为ab>0,所以a,b同号.当a>0,b>0时,$\frac{|a|}{a}+\frac{|b|}{b}-\frac{|ab|}{ab}=1+1-1=1$;当a<0,b<0时,$\frac{|a|}{a}+\frac{|b|}{b}-\frac{|ab|}{ab}=-1-1-1=-3$.综上,$\frac{|a|}{a}+\frac{|b|}{b}-\frac{|ab|}{ab}$的值为1或-3.
3 [2024广州荔湾区期末]在数轴上表示有理数$a,b,c$的点如图所示,已知$a+b<0,ac<0,$给出四个结论:①$abc<0$;②$b+c<0$;③$|a|-|b|>0$;④$|a-c|<|a|$,其中一定成立的结论个数为(
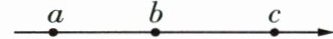
A.1
B.2
C.3
D.4
A
)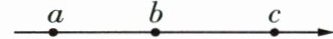
A.1
B.2
C.3
D.4
答案:
3 A 因为ac<0,且点A在点C的左边,所以a<0,c>0.因为a+b<0,且点A在点B的左边,所以|a|>|b|.①b的符号无法确定,故abc<0不一定成立,故①不符合题意;②因为b的符号无法确定,故b+c<0不一定成立,故②不符合题意;③因为|a|>|b|,所以|a|-|b|>0,故③一定成立,符合题意;④因为a<0,c>0,所以原点在点A和点C之间,因为|a-c|表示点A与点C之间的距离,|a|表示点A到原点的距离,所以|a-c|>|a|,故④不成立,不符合题意.综上,一定成立的结论是③,共1个.
4 计算:(1)$-|-0.5|-(-3\frac {1}{4})+2.75-7\frac {1}{2};$
(2)$-\frac {2}{5}÷(-\frac {1}{3})÷(-3\frac {2}{5})×5\frac {2}{3}.$
(2)$-\frac {2}{5}÷(-\frac {1}{3})÷(-3\frac {2}{5})×5\frac {2}{3}.$
答案:
4 解:
(1)-|-0.5|-(-3$\frac{1}{4}$)+2.75-7$\frac{1}{2}$=-$\frac{1}{2}$+3$\frac{1}{4}$+2$\frac{3}{4}$-7$\frac{1}{2}$=(-$\frac{1}{2}$-7$\frac{1}{2}$)+(3$\frac{1}{4}$+2$\frac{3}{4}$)=-8+6=-2.
(2)-$\frac{2}{5}$÷(-$\frac{1}{3}$)÷(-3$\frac{2}{5}$)×5$\frac{2}{3}$=-$\frac{2}{5}$×(-3)×(-$\frac{5}{17}$)×$\frac{17}{3}$=-2.
(1)-|-0.5|-(-3$\frac{1}{4}$)+2.75-7$\frac{1}{2}$=-$\frac{1}{2}$+3$\frac{1}{4}$+2$\frac{3}{4}$-7$\frac{1}{2}$=(-$\frac{1}{2}$-7$\frac{1}{2}$)+(3$\frac{1}{4}$+2$\frac{3}{4}$)=-8+6=-2.
(2)-$\frac{2}{5}$÷(-$\frac{1}{3}$)÷(-3$\frac{2}{5}$)×5$\frac{2}{3}$=-$\frac{2}{5}$×(-3)×(-$\frac{5}{17}$)×$\frac{17}{3}$=-2.
小明的妈妈在某模具厂工作,厂里规定每个工人每周要生产某种模具280个,计划每天生产40个,但由于种种原因,实际每天的生产量与计划量相比有出入。下表是小明妈妈某周的生产情况(超产记为正、减产记为负):

(1)小明的妈妈本周实际生产模具多少个?
(2)该厂实行“每日计件工资制”,每生产一个模具可得工资6元,若超额完成任务,则超过的部分每个另奖3元;若没有完成任务,则少生产一个倒扣2元。小明的妈妈这一周的工资总额是多少元?
(3)在(2)的条件下,①若将实行“每日计件工资制”改为实行“每周计件工资制”,则在此方式下小明的妈妈这一周的工资与按日计件的工资哪一个更多? 请说明理由。
②若按“每周计件工资制”的方式,小明的妈妈这一周的工资要想达到1806元,则她一周需要生产多少个模具?
③若按“每日计件工资制”的方式,且某周中的星期一至星期六每天生产模具的个数分别是45,38,43,40,41,36,小明妈妈这一周的工资要想达到1803元,则她星期日需要生产多少个模具?

(1)小明的妈妈本周实际生产模具多少个?
(2)该厂实行“每日计件工资制”,每生产一个模具可得工资6元,若超额完成任务,则超过的部分每个另奖3元;若没有完成任务,则少生产一个倒扣2元。小明的妈妈这一周的工资总额是多少元?
(3)在(2)的条件下,①若将实行“每日计件工资制”改为实行“每周计件工资制”,则在此方式下小明的妈妈这一周的工资与按日计件的工资哪一个更多? 请说明理由。
②若按“每周计件工资制”的方式,小明的妈妈这一周的工资要想达到1806元,则她一周需要生产多少个模具?
③若按“每日计件工资制”的方式,且某周中的星期一至星期六每天生产模具的个数分别是45,38,43,40,41,36,小明妈妈这一周的工资要想达到1803元,则她星期日需要生产多少个模具?
答案:
(1)(+8)+(-1)+(-4)+(+9)+(-13)+(+7)+0=8-1-4+9-13+7+0=6,280+6=286(个),故小明的妈妈本周实际生产模具286个.
(2)286×6+(8+9+7)×3+(1+4+13)×(-2)=1752(元),故小明的妈妈这一周的工资总额是1752元.
(3)①按日计件的工资更多.理由如下:若实行“每周计件工资制”,则小明的妈妈这一周的工资总额为280×6+6×(6+3)=1734(元).因为1752>1734,所以按日计件的工资更多.
②(1806-280×6)÷(6+3)=14,280+14=294(个),故她一周需要生产294个模具.
③星期一至星期六的工资总额为(45+38+43+40+41+36)×6+(5×3-2×2+3×3+1×3-4×2)=1473(元),所以星期日的工资为1803-1473=330(元),330-40×6=90(元),90÷(6+3)=10(个),40+10=50(个),故她星期日需要生产50个模具.
(1)(+8)+(-1)+(-4)+(+9)+(-13)+(+7)+0=8-1-4+9-13+7+0=6,280+6=286(个),故小明的妈妈本周实际生产模具286个.
(2)286×6+(8+9+7)×3+(1+4+13)×(-2)=1752(元),故小明的妈妈这一周的工资总额是1752元.
(3)①按日计件的工资更多.理由如下:若实行“每周计件工资制”,则小明的妈妈这一周的工资总额为280×6+6×(6+3)=1734(元).因为1752>1734,所以按日计件的工资更多.
②(1806-280×6)÷(6+3)=14,280+14=294(个),故她一周需要生产294个模具.
③星期一至星期六的工资总额为(45+38+43+40+41+36)×6+(5×3-2×2+3×3+1×3-4×2)=1473(元),所以星期日的工资为1803-1473=330(元),330-40×6=90(元),90÷(6+3)=10(个),40+10=50(个),故她星期日需要生产50个模具.
查看更多完整答案,请扫码查看


