第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
11 教材P28思考变式 [2024台州一模]如图,数轴上三个不同的点A,B,P分别表示有理数a,b,$a+b$,则下列关于数轴原点位置的描述正确的是 (

A.原点在点A的左侧
B.原点在A,B两点之间
C.原点在B,P两点之间
D.原点在点P的右侧
A
)
A.原点在点A的左侧
B.原点在A,B两点之间
C.原点在B,P两点之间
D.原点在点P的右侧
答案:
A
12 [2024潮州德芳中学期中]如果两个数的和为负数,那么这两个数一定 (
A.同为正数
B.同为负数
C.至少有一个正数
D.至少有一个负数
D
)A.同为正数
B.同为负数
C.至少有一个正数
D.至少有一个负数
答案:
D 如果两个数的和为负数,那么这两个数可能都是负数,也可能一个是正数,一个是负数,且负数的绝对值较大,还可能一个是0,一个是负数.综上,这两个数一定至少有一个负数.
13 已知有理数a,b,c在数轴上对应点的位置如图所示,下列结论不正确的是 (
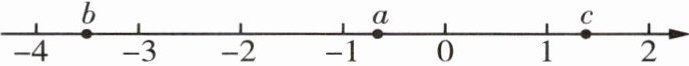
A.$|b|<4$
B.$b+c<0$
C.$a+b>0$
D.$a+c>0$
C
)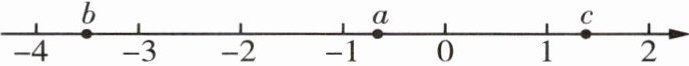
A.$|b|<4$
B.$b+c<0$
C.$a+b>0$
D.$a+c>0$
答案:
C 由题中数轴,可知-4<b<-3,-1<a<0,1<c<2,所以3<|b|<4,b+c<0,a+b<0,a+c>0,所以选项A,B,D不符合题意,选项C符合题意.
14 [2025泉州洛江区期中]用$[x]$表示不超过x的最大整数,如$[2.23]= 2,[-3.24]= -4$,则$[3.3]+[-4.8]$的值为
-2
.
答案:
-2 根据题意,可知[3.3]=3,[-4.8]=-5,所以[3.3]+[-4.8]=3+(-5)=-2.
15 [2025连云港海州区期中]若$|m|= 7,|n|= 3$,且$|m-n|= m-n$,则$m+n$的值是
4或10
.
答案:
4或10 因为|m|=7,|n|=3,所以m=±7,n=±3,又因为|m-n|=m-n,所以m-n≥0,所以m=7,n=±3.当m=7,n=3时,m+n=7+3=10;当m=7,n=-3时,m+n=7+(-3)=4.综上所述,m+n的值为4或10.
16 新趋势·结论开放 已知两个有理数相加,和小于每一个加数,请写出满足上述条件的一个算式:
(-2)+(-3)=-5(答案不唯一)
.
答案:
(-2)+(-3)=-5(答案不唯一)
(1)下列各数对①5和3,②-5和13,③-54和46中,互为“吉祥数”的数对有
(2)在数轴上,点A到原点O的距离是8,请直接写出与点A表示的数互为“吉祥数”的数.
①②
.(只填写序号) (2)在数轴上,点A到原点O的距离是8,请直接写出与点A表示的数互为“吉祥数”的数.
0或16
答案:
解:
(1)①②
①5+3=8,②(-5)+13=8,③(-54)+46=-8,所以①②是"吉祥数"数对.
(2)与点A表示的数互为"吉祥数"的数为0或16.
因为点A到原点O的距离是8,所以点A表示的数为8或-8(提示:分点在原点右侧和左侧两种情况),
当点A表示的数为8时,其"吉祥数"为0;
当点A表示的数为-8时,其"吉祥数"为16.
(1)①②
①5+3=8,②(-5)+13=8,③(-54)+46=-8,所以①②是"吉祥数"数对.
(2)与点A表示的数互为"吉祥数"的数为0或16.
因为点A到原点O的距离是8,所以点A表示的数为8或-8(提示:分点在原点右侧和左侧两种情况),
当点A表示的数为8时,其"吉祥数"为0;
当点A表示的数为-8时,其"吉祥数"为16.
(1)用“<”“>”或“=”填空:
①$|-2|+|3|>|(-2)+3|,|4|+|-1|$
②$|2|+|3|= |2+3|,|-1|+|-3|$
③$|0|+|-8|$
(2)通过以上比较,请你分析、归纳出当a,b为有理数时,$|a|+|b|与|a+b|$的大小关系.
(3)根据(2)中得出的结论,若$|x|+|y|= 10,|x+y|= 8$,求$x-y$的值.
①$|-2|+|3|>|(-2)+3|,|4|+|-1|$
>
$|4+(-1)|;$ ②$|2|+|3|= |2+3|,|-1|+|-3|$
=
$|(-1)+(-3)|;$ ③$|0|+|-8|$
=
$|0+(-8)|.$ (2)通过以上比较,请你分析、归纳出当a,b为有理数时,$|a|+|b|与|a+b|$的大小关系.
当a,b异号时,|a|+|b|>|a+b|;当a,b同号或其中一个为0时,|a|+|b|=|a+b|.综上所述,|a|+|b|≥|a+b|
(3)根据(2)中得出的结论,若$|x|+|y|= 10,|x+y|= 8$,求$x-y$的值.
因为|x|+|y|=10,|x+y|=8,所以|x|+|y|>|x+y|,所以x,y异号(根据(2)的结论可得),所以当x为正数,y为负数时,|x|+|y|=x-y=10;当x为负数,y为正数时,|x|+|y|=(-x)+y=10,即x-y=-10.综上所述,x-y的值为±10
答案:
解:
(1)①>;②=;③=
①因为|4|+|-1|=5,|4+(-1)|=3,所以|4|+|-1|>|4+(-1)|;
②因为|-1|+|-3|=4,|(-1)+(-3)|=4,所以|-1|+|-3|=|(-1)+(-3)|;
③因为|0|+|-8|=8,|0+(-8)|=8,所以|0|+|-8|=|0+(-8)|;
(2)当a,b异号时,|a|+|b|>|a+b|;当a,b同号或其中一个为0时,|a|+|b|=|a+b|.综上所述,|a|+|b|≥|a+b|;
(3)因为|x|+|y|=10,|x+y|=8,所以|x|+|y|>|x+y|,所以x,y异号(根据
(2)的结论可得),所以当x为正数,y为负数时,|x|+|y|=x-y=10;当x为负数,y为正数时,|x|+|y|=(-x)+y=10,即x-y=-10.综上所述,x-y的值为±10.
(1)①>;②=;③=
①因为|4|+|-1|=5,|4+(-1)|=3,所以|4|+|-1|>|4+(-1)|;
②因为|-1|+|-3|=4,|(-1)+(-3)|=4,所以|-1|+|-3|=|(-1)+(-3)|;
③因为|0|+|-8|=8,|0+(-8)|=8,所以|0|+|-8|=|0+(-8)|;
(2)当a,b异号时,|a|+|b|>|a+b|;当a,b同号或其中一个为0时,|a|+|b|=|a+b|.综上所述,|a|+|b|≥|a+b|;
(3)因为|x|+|y|=10,|x+y|=8,所以|x|+|y|>|x+y|,所以x,y异号(根据
(2)的结论可得),所以当x为正数,y为负数时,|x|+|y|=x-y=10;当x为负数,y为正数时,|x|+|y|=(-x)+y=10,即x-y=-10.综上所述,x-y的值为±10.
查看更多完整答案,请扫码查看


