《2025年阳光假日暑假五年级数学人教版》

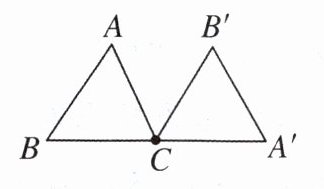
3. 如图,等边三角形$ABC$绕点$C$顺时针旋转$120^{\circ }$后得到三角形$CB'A'$,那么点$A$的对应点是点($A'$),线段$AB$的对应线段是($A'B'$),$∠B$的对应角是($∠B'$),$∠BCB'$是(120)度。

答案： 1. 首先分析对应点：
因为等边三角形$ABC$绕点$C$顺时针旋转$120^{\circ}$后得到三角形$CB'A'$，根据旋转的性质，点$A$绕点$C$旋转后与点$A'$重合，所以点$A$的对应点是点$A'$。
2. 然后分析对应线段：
线段$AB$绕点$C$旋转后与线段$A'B'$重合，所以线段$AB$的对应线段是$A'B'$。
3. 接着分析对应角：
$∠B$绕点$C$旋转后与$∠B'$重合，所以$∠B$的对应角是$∠B'$。
4. 最后求$∠BCB'$的度数：
由于旋转角是$120^{\circ}$，$∠BCB'$就是旋转角，所以$∠BCB' = 120$度。
故答案依次为：$A'$；$A'B'$；$∠B'$；$120$。

二、判断对错。(对的画“√”，错的画“×”)
1. 一个图形旋转后,它的形状与位置都改变了。(×)
2. 明明做了一个标准的“向后转”，他的身体旋转了$90^{\circ }$。(×)
3. 从上午$10:00$到$12:00$,时针旋转了$60^{\circ }$。(√)
4. 将绕点$O$逆时针旋转$90^{\circ }$,得到的图形是。(×)
5. 由连续旋转4次可以得到图形。(×)

答案： 1. ×
2. ×
3. √
4. ×
5. ×

1. 有一个图形,下面(D)是该图形绕点$O$顺时针旋转$90^{\circ }$得到的。

答案： D

2. 不能由经过一次平移或旋转得到的图形是(B)。

答案： B