《2025年阳光假日暑假五年级数学人教版》

4. 阳光小学暑假期间安排王老师每4天值一次班，李老师每6天值一次班，张老师每8天值一次班。如果7月2日他们三人同一天值班，那么下一次他们三人同一天值班是几月几日？(4分)

答案： 【解析】：本题可先求出$4$、$6$、$8$的最小公倍数，这个最小公倍数就是他们三人再次同一天值班间隔的天数。然后根据$7$月的天数，计算出下一次三人同一天值班的日期。
**步骤一：求$4$、$6$、$8$的最小公倍数**
分解质因数法是求最小公倍数的常用方法，先把这几个数分解质因数，再把它们公有的质因数和各自独有的质因数连乘起来，所得的积就是它们的最小公倍数。
$4 = 2×2$；
$6 = 2×3$；
$8 = 2×2×2$。
所以$4$、$6$、$8$的最小公倍数为$2×2×2×3 = 24$，即他们三人每隔$24$天会在同一天值班。
**步骤二：计算下一次三人同一天值班的日期**
已知他们$7$月$2$日同一天值班，再过$24$天会再次同一天值班，$2 + 24 = 26$，所以下一次三人同一天值班是$7$月$26$日。
【答案】：7月26日

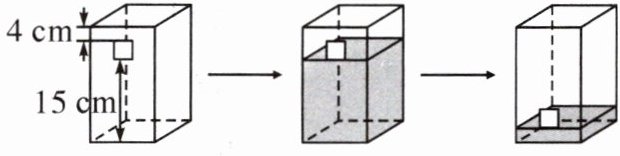
5. 如图，一个长方体容器的一个侧面有一个边长为3cm的正方形开口，往容器里倒了一些水，水刚好无溢出，然后将容器倒过来摆放，水会减少$616cm^{3}$，最初往这个容器里倒了多少立方厘米的水？(容器的厚度忽略不计)(5分)

2310

答案： 【解析】：
- 首先分析容器倒过来摆放水减少的部分：
容器倒过来摆放，水减少的体积是一个底面为边长$3cm$的正方形，高为$(15 + 4)cm$的长方体的体积。根据长方体体积公式$V = a\times b\times h$（这里$a = b=3cm$，$h=(15 + 4)cm$），可算出减少部分体积$V_1=3\times3\times(15 + 4)=3\times3\times19 = 171cm^{3}$。
但题目中说水减少$616cm^{3}$，这里我们设容器底面积为$S$。
当容器正放和倒放时，水减少的体积还可以表示为$S\times4$（因为倒放后水下降的高度对应的体积，从图中可知水下降高度与开口位置有关，这里$616cm^{3}$是水减少的体积，它等于底面积$\times4$），则容器底面积$S=\frac{616}{4}=154cm^{2}$。
- 然后计算最初倒水的体积：
最初倒水的体积等于底面积$\times15$（从图中可知最初水的高度对应的体积，水的高度为$15cm$）加上开口部分没水的体积（开口部分没水的体积是$3\times3\times15$）。
也可以用底面积$\times(15 + 4)-616$来计算。
先算底面积$S = 154cm^{2}$，最初倒水体积$V=154\times(15 + 4)-616$。
先算$154\times(15 + 4)=154\times19 = 2926cm^{3}$，再算$2926-616=2310cm^{3}$。
【答案】：$2310$