《2025年阳光假日暑假五年级数学人教版》

四、计算下面每个图形的表面积。

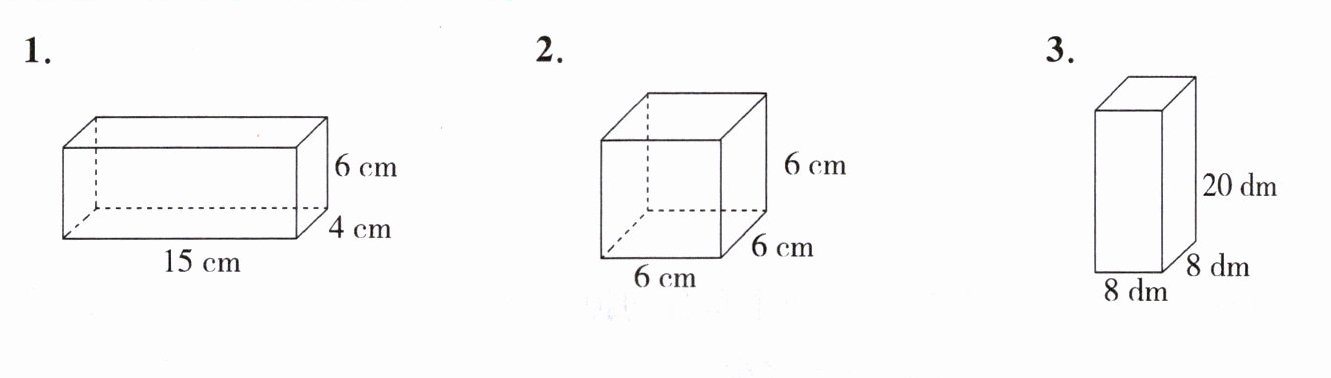
1. (348cm²)
2. (216cm²)
3. (768dm²)

答案： 1. 解：
长方体表面积公式为$S=(ab + ah+bh)\times2$（其中$a = 15\mathrm{cm}$，$b = 4\mathrm{cm}$，$h = 6\mathrm{cm}$）。
则$S=(15\times4 + 15\times6+4\times6)\times2$
先算括号内：$15\times4 = 60$，$15\times6 = 90$，$4\times6 = 24$。
$60 + 90+24=174$。
再算乘法：$174\times2 = 348(\mathrm{cm}^{2})$。
2. 解：
正方体表面积公式为$S = 6a^{2}$（其中$a = 6\mathrm{cm}$）。
则$S=6\times6^{2}$
先算$6^{2}=36$。
再算$6\times36 = 216(\mathrm{cm}^{2})$。
3. 解：
此长方体中$a = 8\mathrm{dm}$，$b = 8\mathrm{dm}$，$h = 20\mathrm{dm}$，根据长方体表面积公式$S=(ab + ah+bh)\times2$。
$S=(8\times8 + 8\times20+8\times20)\times2$
先算括号内：$8\times8 = 64$，$8\times20 = 160$，$8\times20 = 160$。
$64 + 160+160=384$。
再算乘法：$384\times2 = 768(\mathrm{dm}^{2})$。
综上，答案依次为$348\mathrm{cm}^{2}$；$216\mathrm{cm}^{2}$；$768\mathrm{dm}^{2}$。

五、下列图形哪些沿线折叠能围成正方体?剪一剪,折折看。

①③

答案： 【解析】：通过实际剪一剪、折一折的操作（或者根据正方体展开图的特征：正方体展开图有$11$种基本形式，可分为“$1 - 4 - 1$”型、“$2 - 3 - 1$”型、“$2 - 2 - 2$”型、“$3 - 3$”型等，其中“$1 - 4 - 1$”型是最常见的，即中间一行$4$个小正方形，上下各$1$个小正方形；“$2 - 3 - 1$”型是中间$3$个小正方形，上方$2$个小正方形（相连），下方$1$个小正方形等）来判断。
图①是“$2 - 2 - 2$”型展开图，图③是“$1 - 4 - 1$”型展开图，它们沿线折叠能围成正方体；图②不符合正方体展开图的特征，沿线折叠不能围成正方体。
【答案】：①③

1. 一个长方体形状的无盖铁盒,长18cm,宽15cm,高12cm,做这个铁盒至少要用多少铁皮?

答案： 【解析】：本题可根据长方体表面积公式来计算做这个无盖铁盒所需的铁皮面积。由于该铁盒无盖，所以其表面积为$S = ab+(ah + bh)\times2$（其中$a$为长，$b$为宽，$h$为高）。将$a = 18$厘米，$b = 15$厘米，$h = 12$厘米代入公式可得：
$\begin{aligned}S&=18\times15+(18\times12 + 15\times12)\times2\\&=270+(216 + 180)\times2\\&=270 + 396\times2\\&=270 + 792\\&= 1062\end{aligned}$
【答案】：$1062cm^{2}$

2. 小明的爸爸买了2盒中成药,寄给外地的姑姑,药盒外形尺寸如图所示,爸爸想把这些药品包成一个大长方体,请你帮助算一算,最少需要包装纸多少平方厘米?(单位:cm)

1620

答案： 【解析】：
要想使用的包装纸最少，那么就需要把最大的面拼在一起。
已知药盒尺寸$25×10×8$，将两盒包装在一起，此时大长方体的高为$8×2 = 16$厘米。
根据长方体表面积公式$S=(ab + ah + bh)×2$（其中$a = 25$，$b = 10$，$h = 16$）。
$\begin{aligned}S&=(25×10 + 25×16 + 10×16)×2\\&=(250 + 400 + 160)×2\\&=(650 + 160)×2\\&=810×2\\&=1620\end{aligned}$
【答案】：$1620$平方厘米。