《2025年阳光假日暑假五年级数学人教版》

三、找朋友。
$\frac {2}{3}$ $\frac {20}{24}$ $\frac {18}{27}$ $\frac {1}{2}$ $\frac {60}{90}$ $\frac {45}{54}$ $\frac {50}{100}$ $\frac {10}{20}$ $\frac {13}{26}$ $\frac {5}{6}$
1. 与$\frac {10}{12}$相等的分数有($\frac{20}{24}$，$\frac{45}{54}$，$\frac{5}{6}$)。
2. 与$\frac {6}{9}$相等的分数有($\frac{2}{3}$，$\frac{18}{27}$，$\frac{60}{90}$)。
3. 与$\frac {4}{8}$相等的分数有($\frac{1}{2}$，$\frac{50}{100}$，$\frac{10}{20}$，$\frac{13}{26}$)。

答案： 【解析】：本题可先将题目中所给的分数进行约分，化为最简分数，再分别找出与$\frac{10}{12}$、$\frac{6}{9}$、$\frac{4}{8}$相等的分数。
对$\frac{2}{3}$，它已经是最简分数。
对$\frac{20}{24}$进行约分，分子分母同时除以$4$，可得$\frac{20\div4}{24\div4}=\frac{5}{6}$。
对$\frac{18}{27}$进行约分，分子分母同时除以$9$，可得$\frac{18\div9}{27\div9}=\frac{2}{3}$。
$\frac{1}{2}$是最简分数。
对$\frac{60}{90}$进行约分，分子分母同时除以$30$，可得$\frac{60\div30}{90\div30}=\frac{2}{3}$。
对$\frac{45}{54}$进行约分，分子分母同时除以$9$，可得$\frac{45\div9}{54\div9}=\frac{5}{6}$。
对$\frac{50}{100}$进行约分，分子分母同时除以$50$，可得$\frac{50\div50}{100\div50}=\frac{1}{2}$。
对$\frac{10}{20}$进行约分，分子分母同时除以$10$，可得$\frac{10\div10}{20\div10}=\frac{1}{2}$。
对$\frac{13}{26}$进行约分，分子分母同时除以$13$，可得$\frac{13\div13}{26\div13}=\frac{1}{2}$。
$\frac{5}{6}$是最简分数。
对$\frac{10}{12}$进行约分，分子分母同时除以$2$，可得$\frac{10\div2}{12\div2}=\frac{5}{6}$。
对$\frac{6}{9}$进行约分，分子分母同时除以$3$，可得$\frac{6\div3}{9\div3}=\frac{2}{3}$。
对$\frac{4}{8}$进行约分，分子分母同时除以$4$，可得$\frac{4\div4}{8\div4}=\frac{1}{2}$。
然后根据上述约分结果进行分析：
与$\frac{10}{12}$（即$\frac{5}{6}$）相等的分数有$\frac{20}{24}$、$\frac{45}{54}$、$\frac{5}{6}$。
与$\frac{6}{9}$（即$\frac{2}{3}$）相等的分数有$\frac{2}{3}$、$\frac{18}{27}$、$\frac{60}{90}$。
与$\frac{4}{8}$（即$\frac{1}{2}$）相等的分数有$\frac{1}{2}$、$\frac{50}{100}$、$\frac{10}{20}$、$\frac{13}{26}$。
【答案】：1. $\frac{20}{24}$，$\frac{45}{54}$，$\frac{5}{6}$；2. $\frac{2}{3}$，$\frac{18}{27}$，$\frac{60}{90}$；3. $\frac{1}{2}$，$\frac{50}{100}$，$\frac{10}{20}$，$\frac{13}{26}$

四、下面每组中的两个分数是否相等？相等的画“√”，不相等的画“×”。
$\frac {5}{7}$和$\frac {10}{14}$ $\frac {2}{13}$和$\frac {6}{39}$ $\frac {3}{5}$和$\frac {9}{20}$ $\frac {3}{24}$和$\frac {1}{8}$
(√) (√) (×) (√)

答案： √，√，×，√

五、用 2、3、4、6、9、12 这 6 个数字写出 3 个大小相等的分数,每个数字只许用一次。
$\frac{(2)}{(6)}=\frac{(3)}{(9)}=\frac{(4)}{(12)}$;$\frac{(6)}{(2)}=\frac{(9)}{(3)}=\frac{(12)}{(4)}$。

答案： $\frac{2}{6}=\frac{3}{9}=\frac{4}{12}$；$\frac{6}{2}=\frac{9}{3}=\frac{12}{4}$

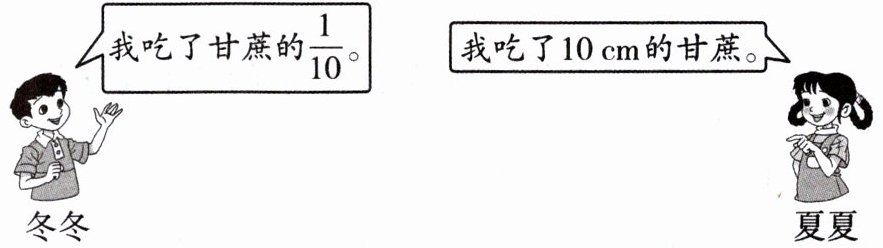
1. 一根 1 m 长的甘蔗。他们俩谁吃的甘蔗多？他们俩吃的甘蔗一样多。

答案： 【解析】：本题可先将甘蔗的长度单位进行换算，再求出冬冬吃的甘蔗长度，最后与夏夏吃的甘蔗长度进行比较。
- **步骤一：单位换算**
已知甘蔗长$1m$，因为$1m = 100cm$，所以将甘蔗长度换算为$100cm$。
- **步骤二：计算冬冬吃的甘蔗长度**
已知冬冬吃了甘蔗的$\frac{1}{10}$，根据分数乘法的意义，求一个数的几分之几是多少用乘法计算，则冬冬吃的甘蔗长度为$100\times\frac{1}{10}= 10$（$cm$）。
- **步骤三：比较两人吃的甘蔗长度**
冬冬吃了$10cm$甘蔗，夏夏也吃了$10cm$甘蔗，$10 = 10$。
【答案】：他们俩吃的甘蔗一样多。