《2025年赢在起跑线中学生快乐暑假七年级数学人教版河北少年儿童出版社》

7. 若关于$x$的不等式组$\begin{cases}\frac{1}{2}x - a ＞ 0, \\ 4 - 2x \geq 0\end{cases}$无解，则$a$的取值范围为$a \geq 1$.

答案： $a \geq 1$

8. 如图所示是一种程序运算，规定：程序运行到“判断结果是否大于 100”为一次运算，若结果大于 100，则输出此结果；若结果不大于 100，则将此结果作为$m$的值再进行第二次运算. 已知运算进行了三次后停止，则$m$的取值范围为$ \frac{121}{8} ＜ m \leq \frac{109}{4} $.

答案： $ \frac{121}{8} ＜ m \leq \frac{109}{4} $

9. 解下列不等式组，并将解集在数轴上表示出来.
(1)$\begin{cases}3x - 5 \leq 1, ① \\ \frac{13 - x}{3} ＜ 4x. ②\end{cases}$
(2)$\begin{cases}2x - 7 ＜ 3(x - 1), ① \\ 5 - \frac{1}{2}(x + 4) \geq x. ②\end{cases}$

答案：
解:
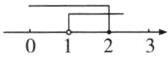
(1) 解不等式①, 得 $x \leq 2$; 解不等式②, 得 $x ＞ 1$. 所以不等式组的解集为 $1 ＜ x \leq 2$. 在数轴上表示如图.
　　　　　　　　
(2) 解不等式①, 得 $x ＞ - 4$; 解不等式②, 得 $x \leq 2$, 所以不等式组的解集为 $ - 4 ＜ x \leq 2$. 在数轴上表示如图.

10. 某公司需将一批材料运往工厂，计划租用甲、乙两种型号的货车，在每辆货车都满载的情况下，若租用 30 辆甲型货车和 50 辆乙型货车可装载 1500 箱材料；若租用 20 辆甲型货车和 60 辆乙型货车可装载 1400 箱材料.
(1) 甲、乙两种型号的货车每辆分别可装载多少箱材料？
(2) 经初步估算，公司要运往工厂的这批材料不得超过 1245 箱. 计划租用甲、乙两种型号的货车共 70 辆，且乙型货车的数量不超过甲型货车数量的 3 倍，该公司一次性将这批材料运往工厂共有哪几种租车方案？

答案： 解:
(1) 设甲型货车每辆可装载 $x$ 箱材料, 乙型货车每辆可装载 $y$ 箱材料.
根据题意, 得 $ \left\{ \begin{array} { l } { 30x + 50y = 1500, } \\ { 20x + 60y = 1400, } \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { x = 25, } \\ { y = 15. } \end{array} \right. $
答: 甲型货车每辆可装载 25 箱材料, 乙型货车每辆可装载 15 箱材料.
(2) 设租用 $m$ 辆甲型货车, 则租用 $(70 - m)$ 辆乙型货车.
根据题意, 得 $ \left\{ \begin{array} { l } { 25m + 15(70 - m) \leq 1245, } \\ { 70 - m \leq 3m, } \end{array} \right. $
解得 $ \frac{35}{2} \leq m \leq \frac{39}{2} $.
又因为 $m$ 为整数, 所以 $m$ 可以取 18, 19,
所以该公司共有 2 种租车方案,
方案 1: 租用 18 辆甲型货车, 52 辆乙型货车;
方案 2: 租用 19 辆甲型货车, 51 辆乙型货车.