2025年赢在起跑线中学生快乐暑假七年级数学人教版河北少年儿童出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在起跑线中学生快乐暑假七年级数学人教版河北少年儿童出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
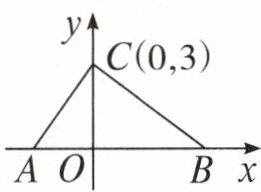
12. 如图,在平面直角坐标系中,点 $ A,B $ 的坐标分别为 $ A(a,0) $,$ B(b,0) $,且 $ a,b $ 满足 $ |a + 2| + (b - 4)^{2} = 0 $,点 $ C $ 的坐标为 $ (0,3) $。
(1) 求 $ a,b $ 的值及 $ S_{\text{三角形}ABC} $。
$ a= $
(2) 若点 $ M $ 在 $ x $ 轴上,且 $ S_{\text{三角形}ACM} = \frac{1}{3}S_{\text{三角形}ABC} $,试求点 $ M $ 的坐标。
点 $ M $ 的坐标为
(1) 求 $ a,b $ 的值及 $ S_{\text{三角形}ABC} $。
$ a= $
-2
,$ b= $4
,$ S_{\text{三角形}ABC}= $9
(2) 若点 $ M $ 在 $ x $ 轴上,且 $ S_{\text{三角形}ACM} = \frac{1}{3}S_{\text{三角形}ABC} $,试求点 $ M $ 的坐标。
点 $ M $ 的坐标为
(0,0)或(-4,0)

答案:
解:
(1)$\because |a+2|+(b-4)^{2}=0,$
$\therefore a+2=0,b-4=0.$
$\therefore a=-2,b=4.\therefore A(-2,0),B(4,0).$
又$\because C(0,3),\therefore AB=|-2-4|=6,CO=3.$
$\therefore S_{\triangle ABC}=\frac {1}{2}AB\cdot CO=\frac {1}{2}×6×3=9.$
(2)设点 M 的坐标为$(x,0),$
则$AM=|x-(-2)|=|x+2|.$
又$\because S_{\triangle ACM}=\frac {1}{3}S_{\triangle ABC},$
$\therefore \frac {1}{2}AM\cdot OC=\frac {1}{3}×9$,即$\frac {1}{2}|x+2|×3=3.$
$\therefore |x+2|=2$,即$x+2=\pm 2,$
解得$x=0$或$x=-4,$
故点 M 的坐标为$(0,0)$或$(-4,0).$
(1)$\because |a+2|+(b-4)^{2}=0,$
$\therefore a+2=0,b-4=0.$
$\therefore a=-2,b=4.\therefore A(-2,0),B(4,0).$
又$\because C(0,3),\therefore AB=|-2-4|=6,CO=3.$
$\therefore S_{\triangle ABC}=\frac {1}{2}AB\cdot CO=\frac {1}{2}×6×3=9.$
(2)设点 M 的坐标为$(x,0),$
则$AM=|x-(-2)|=|x+2|.$
又$\because S_{\triangle ACM}=\frac {1}{3}S_{\triangle ABC},$
$\therefore \frac {1}{2}AM\cdot OC=\frac {1}{3}×9$,即$\frac {1}{2}|x+2|×3=3.$
$\therefore |x+2|=2$,即$x+2=\pm 2,$
解得$x=0$或$x=-4,$
故点 M 的坐标为$(0,0)$或$(-4,0).$
13. 如图,雷达探测器测得六个目标 $ A,B,C,D,E,F $,若目标 $ E,F $ 的位置表示为 $ E(4,300^{\circ}) $,$ F(6,210^{\circ}) $,按照此方法在表示目标 $ A,B,C,D $ 的位置时,其中表示正确的是(
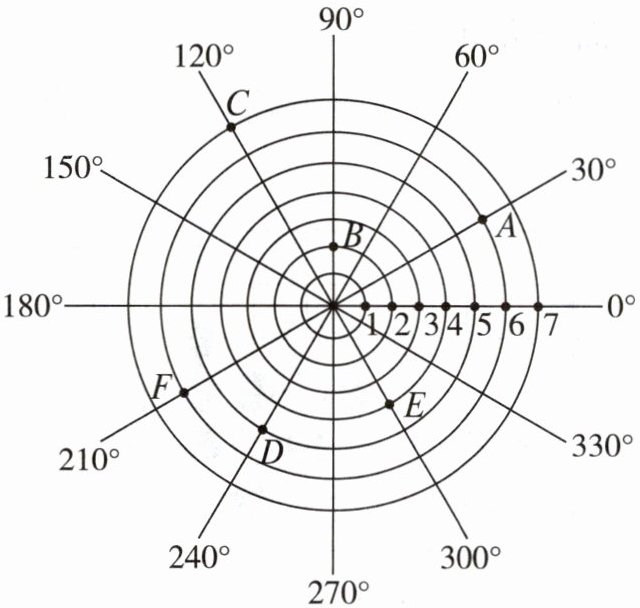
A. $ A(30^{\circ},6) $
B. $ B(1,90^{\circ}) $
C. $ C(120^{\circ},7) $
D. $ D(5,240^{\circ}) $
D
) 
A. $ A(30^{\circ},6) $
B. $ B(1,90^{\circ}) $
C. $ C(120^{\circ},7) $
D. $ D(5,240^{\circ}) $
答案:
D
14. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如 $ a + bi $($ a,b $ 为实数)的数叫作复数,用 $ z = a + bi $ 表示,任何一个复数 $ z = a + bi $ 在平面直角坐标系中都可以用有序数对 $ Z(a,b) $ 表示,如:$ z = 1 + 2i $ 表示为 $ Z(1,2) $,则 $ z = 2 - i $ 可表示为(
A. $ Z(2,0) $
B. $ Z(2,-1) $
C. $ Z(2,1) $
D. $ Z(-1,2) $
B
)A. $ Z(2,0) $
B. $ Z(2,-1) $
C. $ Z(2,1) $
D. $ Z(-1,2) $
答案:
B
查看更多完整答案,请扫码查看


