2025年赢在起跑线中学生快乐暑假七年级数学人教版河北少年儿童出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在起跑线中学生快乐暑假七年级数学人教版河北少年儿童出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
16. 如图,半径为$\frac {1}{2}$的圆周上有一点A落在数轴上-2点处,现将圆在数轴上向右滚动一周后,点A所处的位置在连续整数a,b之间,求$a+b$的平方根.
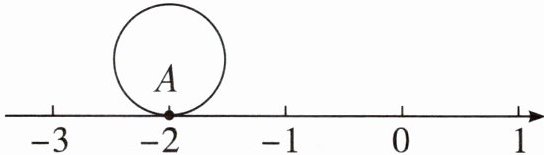
解:∵ 圆的半径为 $ r = \frac{1}{2} $
∴ 圆的周长为 $ C = 2\pi r = $
∵ $ 3 < \pi < 4 $,∴ $ 3 - 2 < \pi - 2 < 4 - 2 $
即 $ 1 < \pi - 2 < 2 $
∴ 向右滚动一周后,点 A 所处的位置在 1 与 2 之间,即 $ a = $
∴ $ a + b = 1 + 2 = $
∴ $ a + b $ 的平方根是
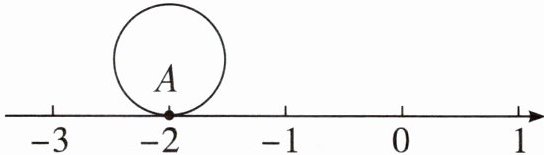
解:∵ 圆的半径为 $ r = \frac{1}{2} $
∴ 圆的周长为 $ C = 2\pi r = $
$\pi$
∵ $ 3 < \pi < 4 $,∴ $ 3 - 2 < \pi - 2 < 4 - 2 $
即 $ 1 < \pi - 2 < 2 $
∴ 向右滚动一周后,点 A 所处的位置在 1 与 2 之间,即 $ a = $
1
,$ b = $2
∴ $ a + b = 1 + 2 = $
3
∴ $ a + b $ 的平方根是
$\pm \sqrt{3}$
答案:
解:
∵ 圆的半径为 $ r = \frac{1}{2} $
∴ 圆的周长为 $ C = 2\pi r = \pi $
∵ $ 3 < \pi < 4 $,
∴ $ 3 - 2 < \pi - 2 < 4 - 2 $
即 $ 1 < \pi - 2 < 2 $
∴ 向右滚动一周后,点 A 所处的位置在 1 与 2 之间,即 $ a = 1 $,$ b = 2 $
∴ $ a + b = 1 + 2 = 3 $
∴ $ a + b $ 的平方根是 $ \pm \sqrt{3} $
∵ 圆的半径为 $ r = \frac{1}{2} $
∴ 圆的周长为 $ C = 2\pi r = \pi $
∵ $ 3 < \pi < 4 $,
∴ $ 3 - 2 < \pi - 2 < 4 - 2 $
即 $ 1 < \pi - 2 < 2 $
∴ 向右滚动一周后,点 A 所处的位置在 1 与 2 之间,即 $ a = 1 $,$ b = 2 $
∴ $ a + b = 1 + 2 = 3 $
∴ $ a + b $ 的平方根是 $ \pm \sqrt{3} $
17. 现有一组有规律的数:$1,-1,\sqrt {2},-\sqrt {2},\sqrt {3},-\sqrt {3},1,-1,\sqrt {2},-\sqrt {2},\sqrt {3},-\sqrt {3},... $,其中$1,-1,\sqrt {2},-\sqrt {2},\sqrt {3},-\sqrt {3}$这六个数按此规律重复出现.
(1)第50个数是什么数?
(2)把从第1个数开始的前2026个数相加,结果是多少?
(3)从第1个数起,把连续若干个数的平方相加,如果和为520,那么一共有多少个数的平方相加?
(1)第50个数是什么数?
(2)把从第1个数开始的前2026个数相加,结果是多少?
(3)从第1个数起,把连续若干个数的平方相加,如果和为520,那么一共有多少个数的平方相加?
答案:
解:
(1)
∵ $ 50 \div 6 = 8 \cdots \cdots 2 $,
∴ 第 50 个数是 -1
(2) $ 2026 \div 6 = 337 \cdots \cdots 4 $
且 $ 1 + (-1) + \sqrt{2} + (-\sqrt{2}) + \sqrt{3} + (-\sqrt{3}) = 0 $
∴ 从第 1 个数开始的前 2026 个数的和是 $ 337 \times 0 + 1 + (-1) + \sqrt{2} + (-\sqrt{2}) = 0 $
(3)
∵ $ 1^2 + (-1)^2 + (\sqrt{2})^2 + (-\sqrt{2})^2 + (\sqrt{3})^2 + (-\sqrt{3})^2 = 12 $,$ 520 \div 12 = 43 \cdots \cdots 4 $,$ 1^2 + (-1)^2 + (\sqrt{2})^2 = 4 $
∴ $ 43 \times 6 + 3 = 261 $,即一共有 261 个数的平方相加
(1)
∵ $ 50 \div 6 = 8 \cdots \cdots 2 $,
∴ 第 50 个数是 -1
(2) $ 2026 \div 6 = 337 \cdots \cdots 4 $
且 $ 1 + (-1) + \sqrt{2} + (-\sqrt{2}) + \sqrt{3} + (-\sqrt{3}) = 0 $
∴ 从第 1 个数开始的前 2026 个数的和是 $ 337 \times 0 + 1 + (-1) + \sqrt{2} + (-\sqrt{2}) = 0 $
(3)
∵ $ 1^2 + (-1)^2 + (\sqrt{2})^2 + (-\sqrt{2})^2 + (\sqrt{3})^2 + (-\sqrt{3})^2 = 12 $,$ 520 \div 12 = 43 \cdots \cdots 4 $,$ 1^2 + (-1)^2 + (\sqrt{2})^2 = 4 $
∴ $ 43 \times 6 + 3 = 261 $,即一共有 261 个数的平方相加
查看更多完整答案,请扫码查看


