《2025年赢在起跑线中学生快乐暑假七年级数学人教版河北少年儿童出版社》

9. 计算$\sqrt [3]{(-1)^{2}}-|1-\sqrt {2}|+\sqrt {16}$的结果为$6 - \sqrt{2}$.

答案： $ 6 - \sqrt{2} $

10. 黄金分割被广泛应用于艺术、建筑、设计等领域. 黄金分割比的确切值为$\frac {\sqrt {5}-1}{2}$，其中$\sqrt {5}-1$介于整数n和$n+1$之间，则n的值是______1.

答案： 1

11. 用“*”表示一种新运算：对于任意正实数a，b，都有$a*b=\sqrt {b}+1$. 例如$8*9=\sqrt {9}+1=4$，那么$15*196=$15，$m*(m*16)=$$\sqrt{5} + 1$.

答案： 15 $ \sqrt{5} + 1 $

12. 计算下列各式的值.
（1）$(\sqrt {3}-\sqrt {10})-2(2\sqrt {10}-\sqrt {3})$.
（2）$-\sqrt [3]{10}+|-\sqrt {5}|+\sqrt {81}+|-\sqrt [3]{10}|$.

答案： 解：
(1) 原式 $ = \sqrt{3} - \sqrt{10} - 4\sqrt{10} + 2\sqrt{3} $
$ = 3\sqrt{3} - 5\sqrt{10} $
(2) 原式 $ = -\sqrt[3]{10} + \sqrt{5} + 9 + \sqrt[3]{10} = \sqrt{5} + 9 $

13. 如图，一只蚂蚁从点A沿数轴向右爬行3个单位长度到达点B，点A表示$-\sqrt {2}$，设点B所表示的数为m.

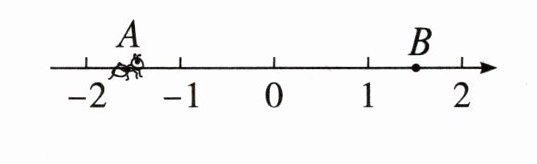
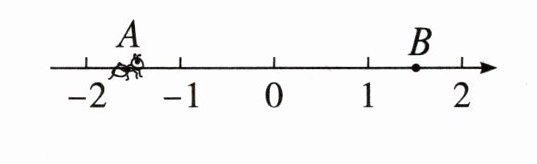
（1）求m的值.
m=$-\sqrt{2}+3$
（2）求$|m-2|+\sqrt {2}+3$的值.
$2\sqrt{2}+2$

答案： 解：
(1) 由题意，得 $ m = -\sqrt{2} + 3 $
(2) $ |m - 2| + \sqrt{2} + 3 = |-\sqrt{2} + 3 - 2| + \sqrt{2} + 3 = \sqrt{2} - 1 + \sqrt{2} + 3 = 2\sqrt{2} + 2 $

14. 对于任意的正数x，y定义运算$\otimes$为：$x\otimes y=\left\{\begin{array}{l} \sqrt {x}-\sqrt {y}(x≥y),\\ \sqrt {x}+\sqrt {y}(x＜y).\end{array}\right. $计算$(2\otimes 3)-(18\otimes 12)$的结果为 ………………………………………………………………………………………（B）
A. $-2\sqrt {2}-\sqrt {3}$
B. $3\sqrt {3}-2\sqrt {2}$
C. $6\sqrt {6}$
D. $-5\sqrt {6}$

答案： B

15. 在1，2，3，…，100这100个自然数的算术平方根和立方根中，无理数有186个.

答案： 186