《2025年快乐暑假天天练数学物理生物》

1. 在下列条件中,能画出平行四边形的是 ()
A. 以 60 cm 为一条对角线、20 cm 和 34 cm 为两条邻边
B. 以 6 cm 和 10 cm 为对角线、8 cm 为一条边
C. 以 20 cm 和 36 cm 为对角线、22 cm 为一条边
D. 以 6 cm 为一条对角线、3 cm 和 10 cm 为两条邻边

答案： C
**选项A：**
已知平行四边形一条对角线为$60cm$，两条邻边分别为$20cm$和$34cm$。
由于平行四边形的两条邻边与一条对角线可构成三角形，而$20 + 34 = 54\lt 60$，不满足三角形三边关系，所以不能画出平行四边形。
**选项B：**
已知平行四边形两条对角线分别为$6cm$和$10cm$，一条边为$8cm$。
因为平行四边形的对角线互相平分，所以两条对角线的一半分别为$6\div2 = 3cm$和$10\div2 = 5cm$。
此时$3 + 5 = 8$，不满足三角形三边关系，所以不能画出平行四边形。
**选项C：**
已知平行四边形两条对角线分别为$20cm$和$36cm$，一条边为$22cm$。
两条对角线的一半分别为$20\div2 = 10cm$和$36\div2 = 18cm$。
因为$10 + 18 = 28\gt 22$，$18 - 10 = 8\lt 22$，满足三角形三边关系，所以能画出平行四边形。
**选项D：**
已知平行四边形一条对角线为$6cm$，两条邻边分别为$3cm$和$10cm$。
$3 + 6 = 9\lt 10$，不满足三角形三边关系，所以不能画出平行四边形。

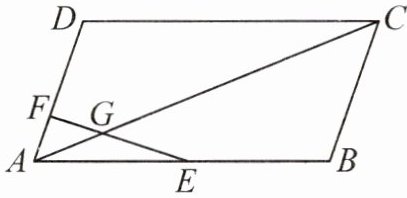
2. 如图,在平行四边形 ABCD 中,E 为 AB 的中点,F 为 AD 上一点,EF 交 AC 于点 G,AF= 2 cm,DF= 4 cm,AG= 3 cm,则 AC 的长为 ()

A. 9 cm
B. 14 cm
C. 15 cm
D. 18 cm

答案： C
本题可通过作辅助线构造相似三角形，再利用相似三角形的性质求出$AC$的长度。
**步骤一：作辅助线**
延长$FE$交$CB$的延长线于点$H$。
因为四边形$ABCD$是平行四边形，所以$AD// BC$，$AD = BC$。
由于$AD// BC$，所以$\angle AFE=\angle H$，$\angle FAE=\angle HBE$。
又因为$E$为$AB$的中点，即$AE = BE$。
根据“角角边”（$AAS$）定理，可得$\triangle AFE\cong\triangle BHE$。
**步骤二：求出$BH$的长度**
由$\triangle AFE\cong\triangle BHE$，根据全等三角形的对应边相等，可得$BH = AF = 2cm$。
已知$AF = 2cm$，$DF = 4cm$，所以$AD=AF + DF=2 + 4 = 6cm$，则$BC = AD = 6cm$。
那么$CH=BH + BC=2 + 6 = 8cm$。
**步骤三：证明$\triangle AFG\sim\triangle CHG$**
因为$AD// BC$，所以$\triangle AFG\sim\triangle CHG$。
**步骤四：根据相似三角形的性质求出$CG$的长度**
根据相似三角形对应边成比例，可得$\frac{AG}{CG}=\frac{AF}{CH}$。
已知$AF = 2cm$，$CH = 8cm$，$AG = 3cm$，代入$\frac{AG}{CG}=\frac{AF}{CH}$可得：
$\frac{3}{CG}=\frac{2}{8}$
交叉相乘可得：$2CG = 3\times8$
即$2CG = 24$，解得$CG = 12cm$。
**步骤五：求出$AC$的长度**
因为$AC = AG + CG$，$AG = 3cm$，$CG = 12cm$，所以$AC = 3 + 12 = 15cm$。

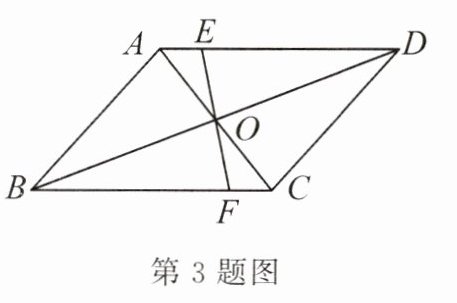
3. 如图,EF 过$□ ABCD$的对角线的交点 O,交 AD 于点 E,交 BC 于点 F,已知 AB= 4,BC= 5,OE= 1.5,那么四边形 EFCD 的周长是 ()


A. 10
B. 11
C. 12
D. 13

答案： C
由于$AD// BC$，则$\angle OAE=\angle OCF$，又因为$\angle AOE=\angle COF$，$OA = OC$，所以$\triangle AOE\cong\triangle COF$（$ASA$）。
所以$OE = OF = 1.5$，$AE = CF$。
那么$DE+CF=DE + AE=AD = 5$。
四边形$EFCD$的周长为$EF + FC+CD + DE=OE + OF+(DE + CF)+CD=1.5 + 1.5+5 + 4 = 12$。

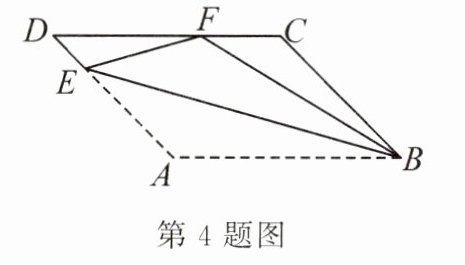
4. 如图,在$□ ABCD$中,点 E 在边 AD 上,以 BE 为折痕,将$\triangle ABE$向上翻折,点 A 正好落在 CD 边上的 F 点处,若$\triangle FDE$的周长为 14, $\triangle FCB$的周长为 22,则 FC 的长度为 ()


A. 4
B. 6
C. 5
D. 3

答案： A
由折叠可知$AE = EF$，$AB = BF$。
$\triangle FDE$的周长为$DE + EF + DF=DE + AE + DF = AD + DF = 14$，即$AD + DF = 14$。
$\triangle FCB$的周长为$FC + BC + BF=FC + AD + AB = 22$，即$FC + AD + CD = 22$。
又因为$CD = DF + FC$，所以$FC + AD+(DF + FC)=22$，把$AD + DF = 14$代入可得$14 + 2FC = 22$，
$2FC=22 - 14$，$2FC = 8$，解得$FC = 4$。