《2025年快乐暑假天天练数学物理生物》

3. 如图,在$□ ABCD$中,AB= 6 cm,$∠BCD$的平分线交 AD 于点 E,则 DE=

答案： $6cm$

4. 如图,把平行四边形 ABCD 折叠,使点 C 与点 A 重合,这时点 D 落在点$D_{1}$处,折痕为 EF,若$∠BAE= 55^{\circ }$,则$∠D_{1}AD= $____.

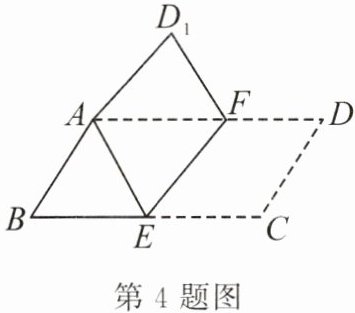
答案： $55^{\circ}$
因为四边形$ABCD$是平行四边形，所以$\angle BAD=\angle C$。
由折叠的性质可知$\angle D_{1}AE = \angle C$，所以$\angle D_{1}AE=\angle BAD$。
那么$\angle D_{1}AD+\angle DAE=\angle BAE+\angle DAE$，所以$\angle D_{1}AD=\angle BAE$。
已知$\angle BAE = 55^{\circ}$。

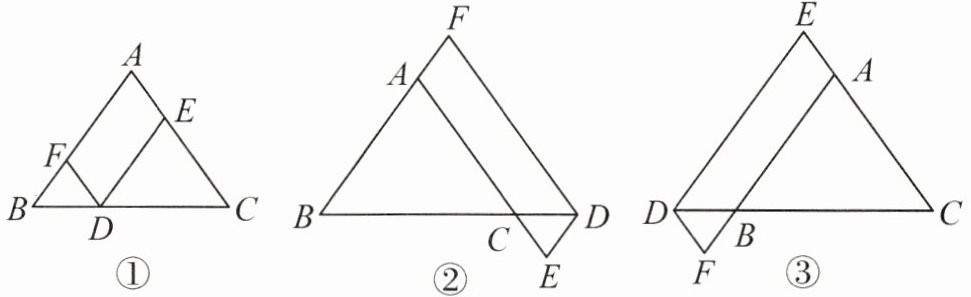
1. 在$\triangle ABC$中,AB= AC,点 D 在边 BC 所在的直线上,过点 D 作 DF$// AC$交直线 AB 于点 F,DE$// AB$交直线 AC 于点 E.
(1)当点 D 在边 BC 上时,如图①,求证:$DE+DF= AC;$
(2)当点 D 在边 BC 的延长线上时,如图②,当点 D 在边 BC 的反向延长线上时,如图③,请分别写出图②、图③中 DE,DF,AC 之间的数量关系,不需要证明;
(3)若 AC= 6,DE= 4,则 DF=

答案： 1. （1）
- 因为$DF// AC$，$DE// AB$，所以四边形$AFDE$是平行四边形，所以$DF = AE$。
- 又因为$DE// AB$，所以$\angle B=\angle EDC$。
- 因为$AB = AC$，所以$\angle B=\angle C$，则$\angle C=\angle EDC$，所以$DE = EC$。
- 那么$DE + DF=EC + AE=AC$。
2. （2）
- 图②：
- 因为$DF// AC$，$DE// AB$，所以四边形$AFDE$是平行四边形，所以$DF = AE$。
- 因为$DE// AB$，所以$\angle ABC=\angle EDC$，又$AB = AC$，所以$\angle ABC=\angle ACB=\angle ECD$，则$\angle EDC=\angle ECD$，所以$DE = EC$。
- 因为$AC = AE-EC$，所以$AC=DF - DE$。
- 图③：
- 因为$DF// AC$，$DE// AB$，所以四边形$AFDE$是平行四边形，所以$DE = AF$。
- 因为$DF// AC$，所以$\angle FDB=\angle C$，又$AB = AC$，所以$\angle ABC=\angle C$，$\angle ABC=\angle FBD$，则$\angle FDB=\angle FBD$，所以$DF = BF$。
- 因为$AC = AB=BF - AF$，所以$AC=DE - DF$。
3. （3）
- 当如图①的情况时，$DF=AC - DE$，已知$AC = 6$，$DE = 4$，则$DF=6 - 4=2$。
- 当如图②的情况时，$DF=AC + DE$，已知$AC = 6$，$DE = 4$，则$DF=6 + 4=10$。
1. （1）证明见上述解析。
2. （2）图②：$AC=DF - DE$；图③：$AC=DE - DF$。
3. （3）$2$或$10$。