《2025年快乐暑假天天练数学物理生物》

1. 已知一组数据75,80,80,85,90,那么这组数据的众数和中位数分别为 ()
A. 75,80
B. 80,85
C. 80,90
D. 80,80

答案： 中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（如果数据个数是奇数），如果数据个数是偶数，则是最中间两个数的平均数。将这组数据75，80，80，85，90从小到大排列为75，80，80，85，90，数据个数是5，为奇数，最中间的数是80，所以中位数是80。
D

2. 九年级某班12名同学练习定点投篮,每人各投10次,进球数量统计如下:

这12名同学进球数的众数是 ()
A. 3.75
B. 3
C. 3.5
D. 7

答案： B

3. 河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是 ()
A. 中位数是12.7%
B. 众数是15.3%
C. 平均数是15.98%
D. 方差是0

答案： 1. 首先明确中位数、众数、平均数和方差的概念：
- 中位数：将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数为这组数据的中位数；如果数据的个数是偶数，则中间两个数据的平均数为这组数据的中位数。
- 众数：一组数据中出现次数最多的数据叫做这组数据的众数。
- 平均数：$\overline{x}=\frac{x_{1} + x_{2}+\cdots+x_{n}}{n}$（$n$表示数据的个数，$x_{1},x_{2},\cdots,x_{n}$表示各个数据）。
- 方差：$s^{2}=\frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots+(x_{n}-\overline{x})^{2}]$，方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立。当一组数据都相等时，方差为$0$。
2. 然后对这组数据$12.7\%$，$14.5\%$，$15.3\%$，$15.3\%$，$17.1\%$进行分析：
- **中位数**：
- 数据个数$n = 5$，是奇数，将数据从小到大排列后，中间的数是$15.3\%$，所以中位数是$15.3\%$，A选项错误。
- **众数**：
- 在这组数据中$15.3\%$出现了$2$次，出现的次数最多，所以众数是$15.3\%$，B选项正确。
- **平均数**：
- $\overline{x}=\frac{12.7\% + 14.5\%+15.3\%+15.3\%+17.1\%}{5}=\frac{(12.7 + 14.5+15.3+15.3+17.1)\%}{5}=\frac{74.9\%}{5}=14.98\%$，C选项错误。
- **方差**：
- 因为这组数据中各个数据不都相等，所以数据有波动，方差不为$0$，D选项错误。
B

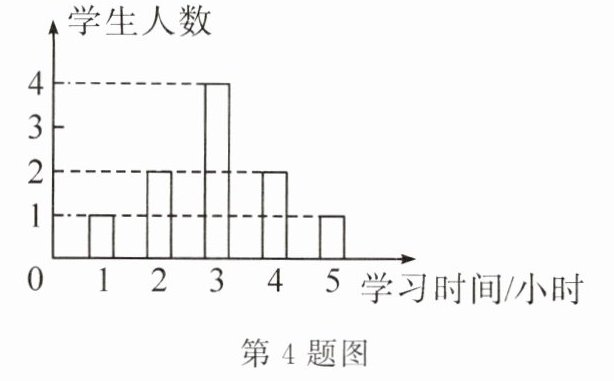
4. 李老师为了解学生周末学习时间的情况,在八(2)班中随机抽查了10名学生,绘制成下页图所示的条形统计图,则这10名学生周末学习的平均时间是 ()


A. 1小时
B. 2小时
C. 3小时
D. 4小时

答案： 加权平均数的计算公式为$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{k}f_{k}}{f_{1}+f_{2}+\cdots +f_{k}}$，其中$x_{1},x_{2},\cdots,x_{k}$表示各数据，$f_{1},f_{2},\cdots,f_{k}$表示各数据的权数。
从条形统计图中可知，学习$1$小时的有$1$人，学习$2$小时的有$2$人，学习$3$小时的有$4$人，学习$4$小时的有$2$人，学习$5$小时的有$1$人。
那么这$10$名学生周末学习的平均时间为：
$\begin{aligned}&\frac{1\times1 + 2\times2 + 3\times4 + 4\times2 + 5\times1}{1 + 2 + 4 + 2 + 1}\\=&\frac{1 + 4 + 12 + 8 + 5}{10}\\=&\frac{30}{10}\\=& 3（小时）\end{aligned}$
C