2025年快乐暑假天天练数学物理生物
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假天天练数学物理生物 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 当$ x = $____时,分式$ \frac { x ^ { 2 } - 9 } { x - 3 } $的值为0.
答案:
先令分子$x^2 - 9 = 0$,根据平方差公式$a^2-b^2=(a+b)(a-b)$,可得$(x + 3)(x - 3)=0$,则$x + 3 = 0$或$x - 3 = 0$,解得$x = - 3$或$x = 3$。
再考虑分母$x - 3\neq0$,即$x\neq3$。
综上,$x$的值只能为$-3$。
$-3$
再考虑分母$x - 3\neq0$,即$x\neq3$。
综上,$x$的值只能为$-3$。
$-3$
2. 某校九(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是____岁.
答案:
$15$
3. 如图,已知O是矩形ABCD对角线的交点,AE平分$ ∠BAD $,$ ∠AOD = 120 ^ { \circ } $,$ ∠AEO = $____.


答案:
因为四边形$ABCD$是矩形,所以$OA = OB$,$\angle BAD=\angle ABC = 90^{\circ}$。
已知$\angle AOD = 120^{\circ}$,则$\angle AOB = 180^{\circ}-\angle AOD=60^{\circ}$,所以$\triangle AOB$是等边三角形,那么$AB = OB$,$\angle ABO = 60^{\circ}$,所以$\angle OBE=\angle ABC - \angle ABO=90^{\circ}-60^{\circ}=30^{\circ}$。
因为$AE$平分$\angle BAD$,$\angle BAD = 90^{\circ}$,所以$\angle BAE=\angle EAD = 45^{\circ}$,则$\triangle ABE$是等腰直角三角形,所以$AB = BE$。
又因为$AB = OB$,所以$OB = BE$,则$\angle OEB=\angle BOE$。
根据三角形内角和为$180^{\circ}$,在$\triangle BOE$中,$\angle OEB=(180^{\circ}-\angle OBE)\div2=(180 - 30)^{\circ}\div2 = 75^{\circ}$。
因为$\angle AEB = 45^{\circ}$,所以$\angle AEO=\angle OEB-\angle AEB=75^{\circ}-45^{\circ}=30^{\circ}$。
$30^{\circ}$
已知$\angle AOD = 120^{\circ}$,则$\angle AOB = 180^{\circ}-\angle AOD=60^{\circ}$,所以$\triangle AOB$是等边三角形,那么$AB = OB$,$\angle ABO = 60^{\circ}$,所以$\angle OBE=\angle ABC - \angle ABO=90^{\circ}-60^{\circ}=30^{\circ}$。
因为$AE$平分$\angle BAD$,$\angle BAD = 90^{\circ}$,所以$\angle BAE=\angle EAD = 45^{\circ}$,则$\triangle ABE$是等腰直角三角形,所以$AB = BE$。
又因为$AB = OB$,所以$OB = BE$,则$\angle OEB=\angle BOE$。
根据三角形内角和为$180^{\circ}$,在$\triangle BOE$中,$\angle OEB=(180^{\circ}-\angle OBE)\div2=(180 - 30)^{\circ}\div2 = 75^{\circ}$。
因为$\angle AEB = 45^{\circ}$,所以$\angle AEO=\angle OEB-\angle AEB=75^{\circ}-45^{\circ}=30^{\circ}$。
$30^{\circ}$
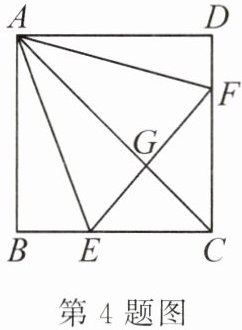
4. 如图,在正方形ABCD中,已知点E,F分别在BC,CD上,$ △AEF $是等边三角形,连接AC交EF于G,给出下列结论:①$ BE = DF $;②$ ∠DAF = 15 ^ { \circ } $;③AC垂直平分EF;④$ BE + DF = EF $.结论正确的有____.(只填序号)

答案:
因为四边形$ABCD$是正方形,所以$AB = AD$,$\angle B=\angle D = 90^{\circ}$。
又因为$\triangle AEF$是等边三角形,所以$AE = AF$。
在$Rt\triangle ABE$和$Rt\triangle ADF$中,$\left\{\begin{array}{l}AB = AD\\AE = AF\end{array}\right.$,根据$HL$定理(斜边和一条直角边对应相等的两个直角三角形全等),可得$Rt\triangle ABE\cong Rt\triangle ADF$,所以$BE = DF$,故①正确。
因为$\triangle AEF$是等边三角形,所以$\angle EAF = 60^{\circ}$,又因为$\angle BAD = 90^{\circ}$,所以$\angle BAE+\angle DAF=90^{\circ}-\angle EAF = 30^{\circ}$。
由$Rt\triangle ABE\cong Rt\triangle ADF$,可得$\angle BAE=\angle DAF$,所以$\angle DAF = 15^{\circ}$,故②正确。
因为$BC = CD$,$BE = DF$,所以$CE = CF$,又因为$AE = AF$,根据线段垂直平分线的判定定理(到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上),可知$AC$垂直平分$EF$,故③正确。
设$EC = x$,由勾股定理可得$EF=\sqrt{2}x$,设$BE = y$,则$AB = x + y$,$AE=\sqrt{(x + y)^{2}+y^{2}}$。
当$x = y$时,$BE+DF = 2y$,$EF=\sqrt{2}y$,$2y\neq\sqrt{2}y$,所以$BE + DF\neq EF$,故④错误。
①②③
又因为$\triangle AEF$是等边三角形,所以$AE = AF$。
在$Rt\triangle ABE$和$Rt\triangle ADF$中,$\left\{\begin{array}{l}AB = AD\\AE = AF\end{array}\right.$,根据$HL$定理(斜边和一条直角边对应相等的两个直角三角形全等),可得$Rt\triangle ABE\cong Rt\triangle ADF$,所以$BE = DF$,故①正确。
因为$\triangle AEF$是等边三角形,所以$\angle EAF = 60^{\circ}$,又因为$\angle BAD = 90^{\circ}$,所以$\angle BAE+\angle DAF=90^{\circ}-\angle EAF = 30^{\circ}$。
由$Rt\triangle ABE\cong Rt\triangle ADF$,可得$\angle BAE=\angle DAF$,所以$\angle DAF = 15^{\circ}$,故②正确。
因为$BC = CD$,$BE = DF$,所以$CE = CF$,又因为$AE = AF$,根据线段垂直平分线的判定定理(到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上),可知$AC$垂直平分$EF$,故③正确。
设$EC = x$,由勾股定理可得$EF=\sqrt{2}x$,设$BE = y$,则$AB = x + y$,$AE=\sqrt{(x + y)^{2}+y^{2}}$。
当$x = y$时,$BE+DF = 2y$,$EF=\sqrt{2}y$,$2y\neq\sqrt{2}y$,所以$BE + DF\neq EF$,故④错误。
①②③
1. 先化简,再求值:$ ( n - \frac { 1 } { n } ) ÷ \frac { n ^ { 2 } - 2 n + 1 } { n } $,其中,$ n = - 3 $.
答案:
本题可先对原式进行化简,再将$n = - 3$代入化简后的式子求值。
**步骤一:化简原式**
- 对$(n - \frac{1}{n})$进行通分:
$n - \frac{1}{n}=\frac{n^2}{n}-\frac{1}{n}=\frac{n^2 - 1}{n}$
- 对$\frac{n^2 - 2n + 1}{n}$的分子进行因式分解:
根据完全平方公式$a^2-2ab+b^2=(a-b)^2$,可得$n^2 - 2n + 1=(n - 1)^2$,则$\frac{n^2 - 2n + 1}{n}=\frac{(n - 1)^2}{n}$。
- 将化简后的式子代入原式并进行除法运算:
$(n - \frac{1}{n}) \div \frac{n^2 - 2n + 1}{n}=\frac{n^2 - 1}{n} \div \frac{(n - 1)^2}{n}$
根据除法运算法则,除以一个数等于乘以它的倒数,则$\frac{n^2 - 1}{n} \div \frac{(n - 1)^2}{n}=\frac{n^2 - 1}{n} \times \frac{n}{(n - 1)^2}$。
对$n^2 - 1$根据平方差公式$a^2-b^2=(a+b)(a-b)$进行因式分解,可得$n^2 - 1=(n + 1)(n - 1)$,则$\frac{n^2 - 1}{n} \times \frac{n}{(n - 1)^2}=\frac{(n + 1)(n - 1)}{n} \times \frac{n}{(n - 1)^2}$。
约分可得$\frac{n + 1}{n - 1}$。
**步骤二:代入求值**
将$n = - 3$代入$\frac{n + 1}{n - 1}$可得:
$\frac{-3 + 1}{-3 - 1}=\frac{-2}{-4}=\frac{1}{2}$
化简结果为$\frac{n + 1}{n - 1}$,值为$\frac{1}{2}$。
**步骤一:化简原式**
- 对$(n - \frac{1}{n})$进行通分:
$n - \frac{1}{n}=\frac{n^2}{n}-\frac{1}{n}=\frac{n^2 - 1}{n}$
- 对$\frac{n^2 - 2n + 1}{n}$的分子进行因式分解:
根据完全平方公式$a^2-2ab+b^2=(a-b)^2$,可得$n^2 - 2n + 1=(n - 1)^2$,则$\frac{n^2 - 2n + 1}{n}=\frac{(n - 1)^2}{n}$。
- 将化简后的式子代入原式并进行除法运算:
$(n - \frac{1}{n}) \div \frac{n^2 - 2n + 1}{n}=\frac{n^2 - 1}{n} \div \frac{(n - 1)^2}{n}$
根据除法运算法则,除以一个数等于乘以它的倒数,则$\frac{n^2 - 1}{n} \div \frac{(n - 1)^2}{n}=\frac{n^2 - 1}{n} \times \frac{n}{(n - 1)^2}$。
对$n^2 - 1$根据平方差公式$a^2-b^2=(a+b)(a-b)$进行因式分解,可得$n^2 - 1=(n + 1)(n - 1)$,则$\frac{n^2 - 1}{n} \times \frac{n}{(n - 1)^2}=\frac{(n + 1)(n - 1)}{n} \times \frac{n}{(n - 1)^2}$。
约分可得$\frac{n + 1}{n - 1}$。
**步骤二:代入求值**
将$n = - 3$代入$\frac{n + 1}{n - 1}$可得:
$\frac{-3 + 1}{-3 - 1}=\frac{-2}{-4}=\frac{1}{2}$
化简结果为$\frac{n + 1}{n - 1}$,值为$\frac{1}{2}$。
查看更多完整答案,请扫码查看


