2025年快乐暑假天天练数学物理生物
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假天天练数学物理生物 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5. 下列关于功、功率、机械效率的说法中正确的是()
A. 做功多的机器,其功率一定高
B. 功率小的机器做功慢
C. 功率大的机器,机械效率一定高
D. 机械效率高的机器做功一定多
A. 做功多的机器,其功率一定高
B. 功率小的机器做功慢
C. 功率大的机器,机械效率一定高
D. 机械效率高的机器做功一定多
答案:
A. 功率是表示做功快慢的物理量,功率的大小等于功与时间的比值,做功多,但时间不确定,其功率不一定高,故A错误;
B. 功率是表示做功快慢的物理量,功率小的机器做功慢,故B正确;
C. 功率和机械效率是两个不同的物理量,功率大的机器,机械效率不一定高,故C错误;
D. 机械效率是有用功与总功的比值,机械效率高说明有用功占总功的比例大,但做功不一定多,故D错误。
B
B. 功率是表示做功快慢的物理量,功率小的机器做功慢,故B正确;
C. 功率和机械效率是两个不同的物理量,功率大的机器,机械效率不一定高,故C错误;
D. 机械效率是有用功与总功的比值,机械效率高说明有用功占总功的比例大,但做功不一定多,故D错误。
B
1. 在水平地面上,工人用100N的水平推力推动重150N的箱子,4s内前进了6m,在这个过程中,木箱所受的重力对木箱做功为______J;工人对木箱做功为______J。
答案:
- 做功的两个必要因素是作用在物体上的力和物体在力的方向上通过的距离。
- 木箱所受重力的方向是竖直向下的,而木箱在水平方向上移动,在重力的方向上没有移动距离,根据$W = Gh$($h$是在重力方向上移动的距离),这里$h = 0$,所以重力对木箱做功$W_{G}=G\times h=150N\times0m = 0J$。
2. 然后分析工人推力做功的情况:
- 已知工人的水平推力$F = 100N$,木箱在推力方向上移动的距离$s = 6m$。
- 根据功的计算公式$W = Fs$,可得工人对木箱做功$W = Fs=100N\times6m = 600J$。
1. $0$ 2. $600$
- 木箱所受重力的方向是竖直向下的,而木箱在水平方向上移动,在重力的方向上没有移动距离,根据$W = Gh$($h$是在重力方向上移动的距离),这里$h = 0$,所以重力对木箱做功$W_{G}=G\times h=150N\times0m = 0J$。
2. 然后分析工人推力做功的情况:
- 已知工人的水平推力$F = 100N$,木箱在推力方向上移动的距离$s = 6m$。
- 根据功的计算公式$W = Fs$,可得工人对木箱做功$W = Fs=100N\times6m = 600J$。
1. $0$ 2. $600$
2. 如图所示,物体重为8N,轻杆可绕O点转动,若要使轻杆在水平位置平衡,在A点应施加的最小力的大小为______N,力的方向为______。
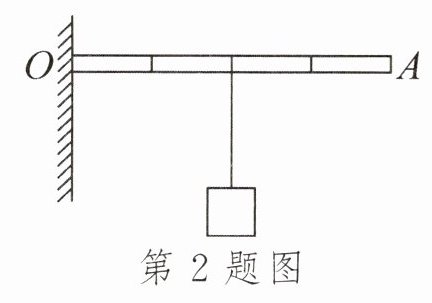

答案:
根据杠杆平衡条件$F_1L_1 = F_2L_2$,在阻力与阻力臂一定时,动力臂越大,动力越小。
由图可知,当力的方向垂直于杠杆$OA$向上(即竖直向上)时,动力臂$L_1$最大,此时动力$F$最小。
设杠杆每一格长度为$L$,则阻力臂$L_2 = 2L$,动力臂$L_1 = 4L$,阻力$F_2=G = 8N$。
根据杠杆平衡条件$F\times L_1=F_2\times L_2$,即$F\times4L = 8N\times2L$,解得$F = 4N$。
$4$;竖直向上
由图可知,当力的方向垂直于杠杆$OA$向上(即竖直向上)时,动力臂$L_1$最大,此时动力$F$最小。
设杠杆每一格长度为$L$,则阻力臂$L_2 = 2L$,动力臂$L_1 = 4L$,阻力$F_2=G = 8N$。
根据杠杆平衡条件$F\times L_1=F_2\times L_2$,即$F\times4L = 8N\times2L$,解得$F = 4N$。
$4$;竖直向上
3. 如图所示,把重力为600N的物体匀速推到斜面顶端,斜面长为3m,高为0.9m,实际推力为300N,那么物体与斜面之间的摩擦力是______N,斜面的机械效率是______。
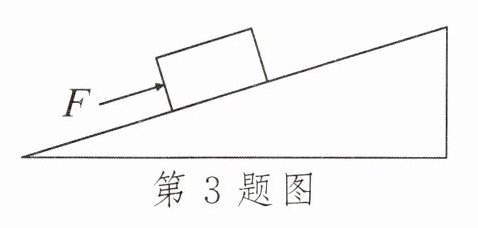

答案:
1. 首先求有用功$W_{有}$:
- 有用功是克服物体重力做的功,根据公式$W_{有}=Gh$(其中$G = 600N$,$h = 0.9m$),可得$W_{有}=600N\times0.9m = 540J$。
2. 然后求总功$W_{总}$:
- 总功是推力做的功,根据公式$W_{总}=Fs$(其中$F = 300N$,$s = 3m$),可得$W_{总}=300N\times3m = 900J$。
3. 接着求额外功$W_{额}$:
- 根据$W_{总}=W_{有}+W_{额}$,可得$W_{额}=W_{总}-W_{有}=900J - 540J = 360J$。
4. 再求摩擦力$f$:
- 额外功是克服摩擦力做的功,$W_{额}=fs$,则$f=\frac{W_{额}}{s}$,把$W_{额}=360J$,$s = 3m$代入可得$f=\frac{360J}{3m}=120N$。
5. 最后求斜面的机械效率$\eta$:
- 根据机械效率公式$\eta=\frac{W_{有}}{W_{总}}\times100\%$,把$W_{有}=540J$,$W_{总}=900J$代入可得$\eta=\frac{540J}{900J}\times100\% = 60\%$。
120;60%
- 有用功是克服物体重力做的功,根据公式$W_{有}=Gh$(其中$G = 600N$,$h = 0.9m$),可得$W_{有}=600N\times0.9m = 540J$。
2. 然后求总功$W_{总}$:
- 总功是推力做的功,根据公式$W_{总}=Fs$(其中$F = 300N$,$s = 3m$),可得$W_{总}=300N\times3m = 900J$。
3. 接着求额外功$W_{额}$:
- 根据$W_{总}=W_{有}+W_{额}$,可得$W_{额}=W_{总}-W_{有}=900J - 540J = 360J$。
4. 再求摩擦力$f$:
- 额外功是克服摩擦力做的功,$W_{额}=fs$,则$f=\frac{W_{额}}{s}$,把$W_{额}=360J$,$s = 3m$代入可得$f=\frac{360J}{3m}=120N$。
5. 最后求斜面的机械效率$\eta$:
- 根据机械效率公式$\eta=\frac{W_{有}}{W_{总}}\times100\%$,把$W_{有}=540J$,$W_{总}=900J$代入可得$\eta=\frac{540J}{900J}\times100\% = 60\%$。
120;60%
4. 某同学利用如图所示装置将重为500N的物体从一楼匀速提升到二楼,他在绳端施加的拉力F= 300N,每层楼高3m,不计绳重和摩擦。他做的有用功为______J,动滑轮重为______N。
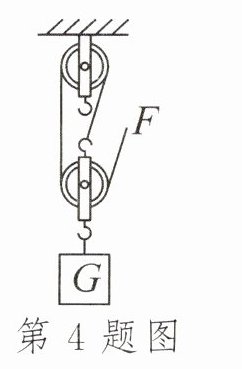

答案:
1. 首先求有用功:
- 有用功是克服物体重力所做的功,根据公式$W_{有}=Gh$,其中$G = 500N$,物体从一楼匀速提升到二楼,每层楼高$3m$,所以$h = 3m$。
- 则$W_{有}=Gh=500N\times3m = 1500J$。
2. 然后求动滑轮重:
- 由图可知,承担物重的绳子股数$n = 2$。
- 不计绳重和摩擦时,根据$F=\frac{G + G_{动}}{n}$,变形可得$G_{动}=nF - G$。
- 已知$F = 300N$,$G = 500N$,$n = 2$,则$G_{动}=2\times300N-500N=600N - 500N = 100N$。
1. $1500$ 2. $100$
- 有用功是克服物体重力所做的功,根据公式$W_{有}=Gh$,其中$G = 500N$,物体从一楼匀速提升到二楼,每层楼高$3m$,所以$h = 3m$。
- 则$W_{有}=Gh=500N\times3m = 1500J$。
2. 然后求动滑轮重:
- 由图可知,承担物重的绳子股数$n = 2$。
- 不计绳重和摩擦时,根据$F=\frac{G + G_{动}}{n}$,变形可得$G_{动}=nF - G$。
- 已知$F = 300N$,$G = 500N$,$n = 2$,则$G_{动}=2\times300N-500N=600N - 500N = 100N$。
1. $1500$ 2. $100$
查看更多完整答案,请扫码查看


