《2025年快乐暑假天天练数学物理生物》

5. 在连接 A 地与 B 地的线段上有四个不同的点 D,G,K,Q,下列四幅图中的实线分别表示某人从 A 地到 B 地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是 ()

答案： B
本题可利用三角形两边之和大于第三边，以及平移的性质来比较各行进路线的长度。
**选项A：**
将$\triangle CDE$平移，使得$CD$与$DE$的部分线段与$AD$、$DB$重合，可发现其行进路线长度等于$AB + 2$倍$\triangle CDE$的某两边（根据平移性质，对应线段相等），但通过后续比较可知不是最长。
- **选项B：**
在$\triangle AFG$中，$AF + FG＞AG$；在$\triangle BGH$中，$BH + HG＞BG$。
行进路线长度为$AF + FG + GH + HB$，因为$AF + FG＞AG$，$BH + HG＞BG$，所以$AF + FG + GH + HB＞AG + BG=AB$。
进一步分析，设$\angle FGA = 180^{\circ}-45^{\circ}-65^{\circ}=70^{\circ}$，$\angle HGB = 180^{\circ}-70^{\circ}-67^{\circ}=43^{\circ}$，通过角度关系和三角形边长关系可知其路线长度大于其他选项。
- **选项C：**
在$\triangle AIK$中，$AI + IK＞AK$；在$\triangle BKM$中，$BM + MK＞ BK$。
行进路线长度为$AI + IK + KM + MB$，$\angle MKB = 180^{\circ}-45^{\circ}-63^{\circ}=72^{\circ}$，但与选项$B$相比，$\angle H = 67^{\circ}$，$\angle M = 63^{\circ}$，根据大角对大边等性质可知其路线不是最长。
- **选项D：**
在$\triangle ANQ$中，$AN + NQ＞AQ$；在$\triangle BQP$中，$BP + PQ＞BQ$。
行进路线长度为$AN + NQ + QP + PB$，$\angle PQB = 180^{\circ}-47^{\circ}-61^{\circ}=72^{\circ}$，$\angle N = 65^{\circ}$，$\angle P = 61^{\circ}$，通过角度与边长关系比较，其路线长度不如选项$B$。

6. 如图,在$□ ABCD$中,AD= 6,AB= 4,DE 平分$∠ADC$交 BC 于点 E,则 BE 的长是()

A. 2
B. 3
C. 4
D. 5

答案： A
因为四边形$ABCD$是平行四边形，根据平行四边形的性质：平行四边形的对边平行且相等，所以$AD// BC$，$BC = AD = 6$，$CD = AB = 4$。
由于$AD// BC$，根据两直线平行，内错角相等，可得$\angle ADE=\angle DEC$。
又因为$DE$平分$\angle ADC$，所以$\angle ADE=\angle EDC$。
从而$\angle DEC=\angle EDC$，根据等角对等边，可知$EC = CD = 4$。
那么$BE=BC - EC$，把$BC = 6$，$EC = 4$代入可得$BE = 6 - 4=2$。

1. 如图,在$□ ABCD$中,对角线 AC,BD 相交于点 O,点 E,F 分别是边 AD,AB 上的点,连接 OE,OF,EF. 若 AB= 7,$BC= 5\sqrt {2},∠DAB= 45^{\circ }$,则$\triangle OEF$周长的最小值是____.

答案： $\frac{13\sqrt{2}}{2}$
作点$O$关于$AD$的对称点$M$，作点$O$关于$AB$的对称点$N$，连接$MN$，分别交$AD$、$AB$于点$E$、$F$，此时$\triangle OEF$的周长最小，周长为$OE + OF + EF=ME + EF + FN = MN$。
因为四边形$ABCD$是平行四边形，所以$OA = OC$，$OB = OD$，$AD// BC$。
已知$AB = 7$，$BC = 5\sqrt{2}$，$\angle DAB = 45^{\circ}$，根据平行四边形的性质$AD = BC = 5\sqrt{2}$。
由于点$M$与点$O$关于$AD$对称，点$N$与点$O$关于$AB$对称，所以$AM = AO$，$AN = AO$，$\angle MAD=\angle OAD$，$\angle NAB=\angle OAB$。
因为$\angle DAB = 45^{\circ}$，所以$\angle MAN = 2\angle DAB=90^{\circ}$。
过点$D$作$DH\perp AB$于点$H$，在$Rt\triangle ADH$中，$\angle DAB = 45^{\circ}$，$AD = 5\sqrt{2}$，根据三角函数$\sin\angle DAB=\frac{DH}{AD}$，$\cos\angle DAB=\frac{AH}{AD}$，可得$DH = AH = AD\sin45^{\circ}=5\sqrt{2}×\frac{\sqrt{2}}{2}=5$。
$HB=AB - AH=7 - 5 = 2$，在$Rt\triangle BDH$中，根据勾股定理$BD=\sqrt{DH^{2}+HB^{2}}=\sqrt{5^{2}+2^{2}}=\sqrt{25 + 4}=\sqrt{29}$。
又因为平行四边形对角线互相平分，所以$AO = OC$，$BO = OD=\frac{1}{2}BD$，$AM = AN = AO$。
根据平行四边形的性质$AC^{2}+BD^{2}=2(AB^{2}+BC^{2})$（平行四边形对角线平方和等于四条边平方和），将$AB = 7$，$BC = 5\sqrt{2}$代入可得：
$AC^{2}+(\sqrt{29})^{2}=2(7^{2}+(5\sqrt{2})^{2})$
$AC^{2}+29 = 2(49 + 50)$
$AC^{2}+29 = 198$
$AC^{2}=169$
$AC = 13$，则$AO=\frac{1}{2}AC=\frac{13}{2}$，所以$AM = AN=\frac{13}{2}$。
在$Rt\triangle MAN$中，根据勾股定理$MN=\sqrt{AM^{2}+AN^{2}}=\sqrt{(\frac{13}{2})^{2}+(\frac{13}{2})^{2}}=\frac{13\sqrt{2}}{2}$。

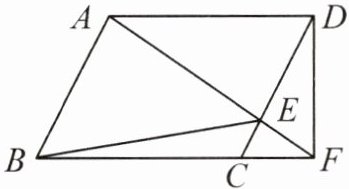
2. 如图,在$□ ABCD$中,点 E 在 CD 边上运动(不与 C,D 两点重合),连接 AE 并延长与 BC 的延长线交于点 F,连接 BE,DF. 若$\triangle BCE$的面积为 8,则$\triangle DEF$的面积为____.

答案： 8
因为四边形$ABCD$是平行四边形，所以$AD// BC$，$AB// CD$。
根据平行四边形的性质，$\triangle ADE$和$\triangle BCE$的高相等（设为$h_1$），$\triangle ABE$和$\triangle DCE$的高相等（设为$h_2$）。
$S_{\triangle ADF}=S_{\triangle ADE}+S_{\triangle DEF}$，$S_{\triangle ABF}=S_{\triangle ABE}+S_{\triangle BEF}$。
由于$AD// BC$，所以$S_{\triangle ADF}=S_{\triangle ABD}$（等底等高，$AD$为底，$AD$与$BC$间的距离为高），又因为$S_{\triangle ABD}=S_{\triangle ABC}$（平行四边形对角线平分面积）。
$S_{\triangle ABC}=S_{\triangle ABE}+S_{\triangle BCE}$，$S_{\triangle BEF}=S_{\triangle BCE}+S_{\triangle DEF}$（因为$S_{\triangle ADF}=S_{\triangle ABF}$，$S_{\triangle ADF}=S_{\triangle ADE}+S_{\triangle DEF}$，$S_{\triangle ABF}=S_{\triangle ABE}+S_{\triangle BEF}$，且$S_{\triangle ADE}=S_{\triangle ABE}$（$\triangle ADE$和$\triangle ABE$ 分别以$DE$、$BE$为底时，高$h_2$相等，$DE = BE$？ 不对，换个思路：
因为$AB// CD$，所以$S_{\triangle ADE}=S_{\triangle BDE}$（等底等高，以$DE$为底，$AB$与$CD$间距离为高）。
$S_{\triangle ADF}=S_{\triangle ADE}+S_{\triangle DEF}$，$S_{\triangle BCF}=S_{\triangle BCE}+S_{\triangle BEF}$，又因为$AD// BC$，$S_{\triangle ADF}=S_{\triangle BCF}$（$\triangle ADF$和$\triangle BCF$分别以$AD$、$BC$为底，$AD$与$BC$间距离为高，$AD = BC$）。
$S_{\triangle ADE}=S_{\triangle BDE}$，那么$S_{\triangle DEF}=S_{\triangle BCE}$。