《2025年快乐暑假天天练数学物理生物》

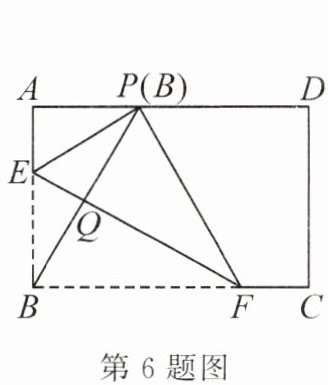
6. 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且$AE= \frac {1}{3}AB$,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.对于下列结论:①$EF= 2BE$;②$PF= 2PE$;③$FQ= 4EQ$;④$\triangle PBF$是等边三角形.正确的是 ()

A. ①②
B. ②③
C. ①③
D. ①④

答案： - 因为$AE=\frac{1}{3}AB$，所以$BE = 2AE$。
由折叠性质可知$PE = BE$，$\angle APE+\angle AEP = 90^{\circ}$，$\angle AEP+\angle BEF = 90^{\circ}$，所以$\angle APE=\angle BEF$。
又因为$\angle A=\angle EBF = 90^{\circ}$，所以$\triangle APE\sim\triangle BEF$，则$\frac{AE}{BF}=\frac{PE}{EF}$。
因为$PE = BE = 2AE$，所以$\frac{AE}{BF}=\frac{2AE}{EF}$，即$EF = 2BF$。
在$Rt\triangle BEF$中，$\angle EBF = 90^{\circ}$，$EF = 2BF$，所以$\angle BEF = 30^{\circ}$，则$EF = 2BE$，故①**正确**。
- 在$Rt\triangle PEF$中，$\angle EPF = \angle EBF = 90^{\circ}$，$\angle PEF=\angle BEF = 30^{\circ}$，所以$PF=\sqrt{3}PE$，故②**错误**。
- 由折叠可知$EF\perp BP$，$\angle EBQ=\angle BEF = 30^{\circ}$，所以$BE = 2EQ$，又因为$EF = 2BE$，所以$EF = 4EQ$，则$FQ = 3EQ$，故③**错误**。
- 由折叠可知$PB = PF$，$\angle EFB=\angle EFP = 60^{\circ}$，所以$\angle PFB = 60^{\circ}$，则$\triangle PBF$是等边三角形，故④**正确**。
D

1. 一个纳米粒子的直径为35纳米,若用科学记数法表示,则为____米.(1纳米$=10^{-9}$米)

答案： $3.5\times10^{-8}$

2. 若$x^{2}-2x= 1$,则$x^{2}+x^{-2}= $____.

答案： **步骤一：由$x^{2}-2x = 1$求出$x - \frac{1}{x}$的值**
已知$x^{2}-2x = 1$，因为$x = 0$时，$x^{2}-2x = 0\neq1$，所以$x\neq0$。
等式两边同时除以$x$，可得$x - 2 = \frac{1}{x}$，移项得到$x - \frac{1}{x} = 2$。
**步骤二：根据完全平方公式求出$x^{2}+x^{-2}$的值**
根据负指数幂的定义可知$x^{-2}=\frac{1}{x^{2}}$，所以$x^{2}+x^{-2}=x^{2}+\frac{1}{x^{2}}$。
对$x - \frac{1}{x} = 2$两边同时平方，根据完全平方公式$(a-b)^2=a^2-2ab+b^2$可得$(x - \frac{1}{x})^2 = 2^2$，即$x^{2}-2\times x\times\frac{1}{x}+\frac{1}{x^{2}} = 4$，化简可得$x^{2}-2+\frac{1}{x^{2}} = 4$。
移项可得$x^{2}+\frac{1}{x^{2}} = 4 + 2 = 6$，即$x^{2}+x^{-2}= 6$。
$6$

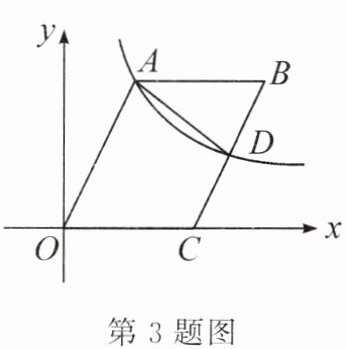
3. 如图,以$//ogram ABCO$的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A,C的坐标分别是$(2,4),(3,0)$,过点A的反比例函数$y= \frac {k}{x}$的图象交BC于D,连接AD,则四边形AOCD的面积是____.

答案： 首先求反比例函数表达式：
已知$A(2,4)$在反比例函数$y = \frac{k}{x}$的图象上，将$A(2,4)$代入$y=\frac{k}{x}$，根据反比例函数$k = xy$，可得$k=2\times4 = 8$，所以反比例函数解析式为$y=\frac{8}{x}$。
然后求$B$点坐标：
因为四边形$ABCO$是平行四边形，$O(0,0)$，$C(3,0)$，$A(2,4)$，根据平行四边形对边平行且相等，可得$B$点坐标为$(2 + 3,4)$，即$B(5,4)$。
接着求直线$BC$的解析式：
设直线$BC$的解析式为$y=mx + n$，把$B(5,4)$，$C(3,0)$代入$y = mx + n$得$\begin{cases}5m + n=4\\3m + n=0\end{cases}$，
用$5m + n=4$减去$3m + n=0$：$(5m + n)-(3m + n)=4 - 0$，
即$5m + n-3m - n=4$，$2m=4$，解得$m = 2$。
把$m = 2$代入$3m + n=0$，得$3\times2 + n=0$，$n=-6$。
所以直线$BC$的解析式为$y = 2x-6$。
再求$D$点坐标：
联立$\begin{cases}y = 2x-6\\y=\frac{8}{x}\end{cases}$，即$2x-6=\frac{8}{x}$，
方程两边同乘$x$得$2x^{2}-6x - 8 = 0$，化简为$x^{2}-3x - 4 = 0$，
分解因式得$(x - 4)(x+1)=0$，解得$x_{1}=4$，$x_{2}=-1$（舍去，因为$D$在第一象限）。
当$x = 4$时，$y=\frac{8}{4}=2$，所以$D(4,2)$。
最后求四边形$AOCD$的面积：
$S_{//ogram ABCO}=OC\times y_{A}=3\times4 = 12$，
$S_{\triangle ABD}=\frac{1}{2}\times(5 - 4)\times(4 - 2)=1$，
所以$S_{四边形AOCD}=S_{//ogram ABCO}-S_{\triangle ABD}=12 - 1=11$。
$11$