《2025年快乐暑假天天练数学物理生物》

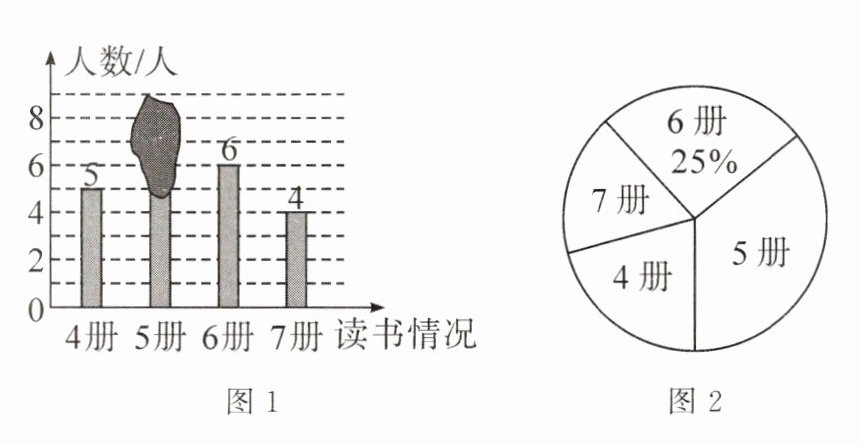
1. 老师随机抽查了本学期学生阅读课外书册数的情况,绘制成条形统计图(如图1)和不完整的扇形统计图(如图2),其中条形统计图被墨迹遮盖了一部分.
(1)求条形统计图中被遮盖的数,并写出册数的中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没有改变,则最多补查了____人.

答案： $(1)$求被遮盖的数和册数的中位数
- **步骤一：计算抽查的总人数**
已知读$6$册的人数为$6$人，且读$6$册的人数占总人数的$25\%$，根据“部分量$\div$该部分量所占百分比$=$总量”，可得抽查的总人数为$6\div25\% = 24$人。
- **步骤二：计算被遮盖的数（读$5$册的人数）**
已知读$4$册的有$5$人，读$6$册的有$6$人，读$7$册的有$4$人，那么读$5$册的人数为$24-(5 + 6 + 4)=24 - 15 = 9$人。
- **步骤三：求册数的中位数**
将数据从小到大排列：$4$册、$4$册、$\cdots$（$5$个$4$册），$5$册、$5$册、$\cdots$（$9$个$5$册），$6$册、$6$册、$\cdots$（$6$个$6$册），$7$册、$7$册、$\cdots$（$4$个$7$册）。
总共有$24$个数据，中位数是第$12$、$13$个数据的平均数，第$12$、$13$个数据都是$5$册，所以中位数是$5$册。
$(2)$计算最多补查的人数
- 原来的数据有$24$个，中位数是第$12$、$13$个数据的平均数（$5$册）。
- 补查后中位数不变，因为最少读了$6$册，要使中位数不变，那么补查后数据的个数最多为$27$个（此时第$14$、$15$个数据还是$5$册）。
- 所以最多补查了$27 - 24 = 3$人。
$(1)$被遮盖的数是$9$，册数的中位数是$5$册；$(2)3$。

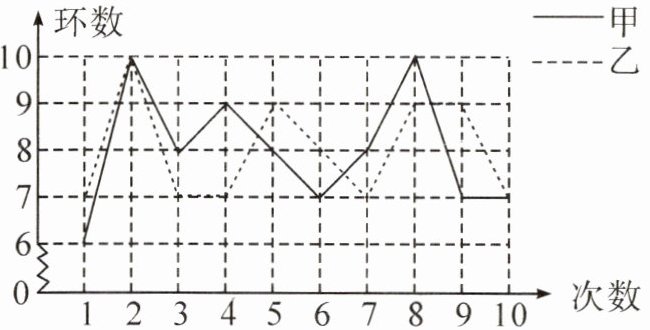
2. 甲、乙两名射击运动员进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.
根据图中信息,回答下列问题:
(1)甲的平均数是____,乙的中位数是____;
(2)分别计算甲、乙成绩的方差,从计算结果来分析,你认为哪位运动员的射击成绩更稳定?

答案： （1）计算甲的平均数和乙的中位数
- **计算甲的平均数：**
根据平均数公式$\bar{x}=\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}$（其中$n$是数据个数，$x_{i}$是第$i$个数据）。
甲射击$10$次的成绩分别为$6$、$10$、$8$、$9$、$8$、$7$、$8$、$10$、$7$、$7$。
则甲的平均数$\bar{x}_{甲}=\frac{6 + 10 + 8 + 9 + 8 + 7 + 8 + 10 + 7 + 7}{10}=\frac{80}{10}=8$。
- **计算乙的中位数：**
将乙射击$10$次的成绩从小到大排列：$7$、$7$、$7$、$7$、$8$、$9$、$9$、$9$、$10$、$10$。
中位数是按顺序排列的一组数据中居于中间位置的数，如果数据有奇数个，则正中间的数字为中位数；如果数据有偶数个，则中间两位数的平均数为中位数。
这里$n = 10$（偶数），中间的两个数是第$5$个数和第$6$个数，即$8$和$9$。
所以乙的中位数$=\frac{8 + 9}{2}=8.5$。
（2）计算甲、乙成绩的方差并比较稳定性
方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$。
- **计算甲的方差：**
$\bar{x}_{甲}=8$，$n = 10$。
$s_{甲}^{2}=\frac{1}{10}[(6 - 8)^{2}+(10 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}+(7 - 8)^{2}+(8 - 8)^{2}+(10 - 8)^{2}+(7 - 8)^{2}+(7 - 8)^{2}]$
$=\frac{1}{10}[(-2)^{2}+2^{2}+0^{2}+1^{2}+0^{2}+(-1)^{2}+0^{2}+2^{2}+(-1)^{2}+(-1)^{2}]$
$=\frac{1}{10}(4 + 4+0 + 1+0 + 1+0 + 4+1 + 1)$
$=\frac{1}{10}\times16 = 1.6$。
- **计算乙的平均数：**
乙射击$10$次的成绩分别为$7$、$7$、$7$、$7$、$8$、$9$、$9$、$9$、$10$、$10$。
$\bar{x}_{乙}=\frac{7 + 7 + 7 + 7 + 8 + 9 + 9 + 9 + 10 + 10}{10}=\frac{83}{10}=8.3$。
- **计算乙的方差：**
$s_{乙}^{2}=\frac{1}{10}[(7 - 8.3)^{2}+(7 - 8.3)^{2}+(7 - 8.3)^{2}+(7 - 8.3)^{2}+(8 - 8.3)^{2}+(9 - 8.3)^{2}+(9 - 8.3)^{2}+(9 - 8.3)^{2}+(10 - 8.3)^{2}+(10 - 8.3)^{2}]$
$=\frac{1}{10}[(-1.3)^{2}+(-1.3)^{2}+(-1.3)^{2}+(-1.3)^{2}+(-0.3)^{2}+0.7^{2}+0.7^{2}+0.7^{2}+1.7^{2}+1.7^{2}]$
$=\frac{1}{10}(1.69+1.69+1.69+1.69+0.09+0.49+0.49+0.49+2.89+2.89)$
$=\frac{1}{10}\times13.3 = 1.33$。
因为方差越小，数据的波动越小，成绩越稳定，$s_{甲}^{2}=1.6$，$s_{乙}^{2}=1.33$，$s_{甲}^{2}＞s_{乙}^{2}$，所以乙运动员的射击成绩更稳定。
(1) $8$；$8.5$
(2) 甲的方差$s_{甲}^{2}=1.6$，乙的方差$s_{乙}^{2}=1.33$，乙运动员的射击成绩更稳定。