2025年快乐暑假天天练数学物理生物
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假天天练数学物理生物 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列有理式:$\frac {x-1}{3},\frac {b^{2}}{a+1},\frac {2x+y}{π},-\frac {1}{m-2},\frac {1}{2}+a,\frac {(x-y)^{2}}{(x+y)^{2}},2-\frac {1}{x},-\frac {5}{11}$.分式共有 ()
A. 2个
B. 3个
C. 4个
D. 5个
A. 2个
B. 3个
C. 4个
D. 5个
答案:
C
2. 函数$y= \frac {\sqrt {1+2x}}{x-1}$中,自变量x的取值范围是 ()
A.$x≥-\frac {1}{2}$
B.$x≠1$
C.$x>1$
D.$x≥-\frac {1}{2}且x≠1$
A.$x≥-\frac {1}{2}$
B.$x≠1$
C.$x>1$
D.$x≥-\frac {1}{2}且x≠1$
答案:
D
3. 已知直线$y= kx-2经过点(3,1)$,则这条直线还经过的点是下面的 ()
A.$(2,0)$
B.$(0,2)$
C.$(1,3)$
D.$(3,-1)$
A.$(2,0)$
B.$(0,2)$
C.$(1,3)$
D.$(3,-1)$
答案:
选项A:当$x = 2$时,$y = 2 - 2 = 0$,所以点$(2,0)$在直线上。
选项B:当$x = 0$时,$y = 0 - 2 = -2\neq2$,所以点$(0,2)$不在直线上。
选项C:当$x = 1$时,$y = 1 - 2 = -1\neq3$,所以点$(1,3)$不在直线上。
选项D:当$x = 3$时,$y = 3 - 2 = 1\neq -1$,所以点$(3,-1)$不在直线上。
A
选项B:当$x = 0$时,$y = 0 - 2 = -2\neq2$,所以点$(0,2)$不在直线上。
选项C:当$x = 1$时,$y = 1 - 2 = -1\neq3$,所以点$(1,3)$不在直线上。
选项D:当$x = 3$时,$y = 3 - 2 = 1\neq -1$,所以点$(3,-1)$不在直线上。
A
4. 某校对部分参加夏令营的中学生的年龄(单位:岁)进行统计,结果如下表:

则这些学生年龄的众数和中位数分别是 ()
A. 16,15
B. 16,14
C. 15,15
D. 14,15

则这些学生年龄的众数和中位数分别是 ()
A. 16,15
B. 16,14
C. 15,15
D. 14,15
答案:
众数是一组数据中出现次数最多的数据。在这组数据中,$16$岁出现的次数最多($3$次),所以众数是$16$。
中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(如果数据个数是奇数),或者最中间两个数的平均数(如果数据个数是偶数)。
- 首先计算总人数:$1 + 2 + 2 + 3 + 1=9$(人),$9$是奇数。
- 然后将年龄从小到大排列:$13$,$14$,$14$,$15$,$15$,$16$,$16$,$16$,$17$。
- 最中间的数是第$5$个数,即$15$,所以中位数是$15$。
A
中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(如果数据个数是奇数),或者最中间两个数的平均数(如果数据个数是偶数)。
- 首先计算总人数:$1 + 2 + 2 + 3 + 1=9$(人),$9$是奇数。
- 然后将年龄从小到大排列:$13$,$14$,$14$,$15$,$15$,$16$,$16$,$16$,$17$。
- 最中间的数是第$5$个数,即$15$,所以中位数是$15$。
A
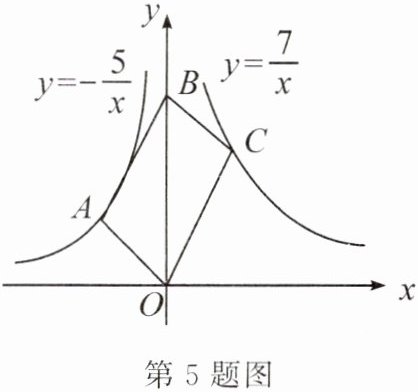
5. 如图,平行四边形OABC的顶点O,B在y轴上,顶点A在反比例函数$y= -\frac {5}{x}$上,顶点C在反比例函数$y= \frac {7}{x}$上,则平行四边形OABC的面积是 ()
A. 8
B. 10
C. 12
D.$\frac {31}{2}$

A. 8
B. 10
C. 12
D.$\frac {31}{2}$
答案:
过点$A$作$AD\perp y$轴于点$D$,过点$C$作$CE\perp y$轴于点$E$。
因为四边形$OABC$是平行四边形,所以$OA = BC$,$OA// BC$,则$\angle AOD=\angle CBE$。
又因为$\angle ADO=\angle BEC = 90^{\circ}$,所以$\triangle AOD\cong\triangle CBE(AAS)$。
根据反比例函数$k$的几何意义:对于反比例函数$y=\frac{k}{x}(k\neq0)$,过双曲线上任意一点作$x$轴、$y$轴的垂线,所得矩形的面积为$\vert k\vert$,三角形的面积为$\frac{1}{2}\vert k\vert$。
对于$y = -\frac{5}{x}$,$S_{\triangle AOD}=\frac{1}{2}\times\vert - 5\vert=\frac{5}{2}$;对于$y=\frac{7}{x}$,$S_{\triangle OCE}=\frac{1}{2}\times\vert7\vert=\frac{7}{2}$。
$S_{矩形ODCE}=S_{\triangle AOD}+S_{四边形ADCB}+S_{\triangle OCE}$,$S_{//ogram OABC}=S_{四边形ADCB}+S_{\triangle AOD}+S_{\triangle BEC}$,又因为$\triangle AOD\cong\triangle CBE$,所以$S_{//ogram OABC}=S_{\triangle AOD}+S_{\triangle OCE}+S_{四边形ADCB}=S_{矩形ODCE}$。
$S_{矩形ODCE}=\frac{5}{2}+\frac{7}{2}+S_{四边形ADCB}$,而$S_{//ogram OABC}=S_{\triangle AOD}+S_{\triangle BEC}+S_{四边形ADCB}$,因为$\triangle AOD\cong\triangle CBE$,所以$S_{//ogram OABC}=\frac{1}{2}\times\vert - 5\vert+\frac{1}{2}\times\vert7\vert+\frac{1}{2}\times\vert - 5\vert+\frac{1}{2}\times\vert7\vert$
$S_{//ogram OABC}=\frac{5 + 7}{2}+\frac{5 + 7}{2}=12$。
C
因为四边形$OABC$是平行四边形,所以$OA = BC$,$OA// BC$,则$\angle AOD=\angle CBE$。
又因为$\angle ADO=\angle BEC = 90^{\circ}$,所以$\triangle AOD\cong\triangle CBE(AAS)$。
根据反比例函数$k$的几何意义:对于反比例函数$y=\frac{k}{x}(k\neq0)$,过双曲线上任意一点作$x$轴、$y$轴的垂线,所得矩形的面积为$\vert k\vert$,三角形的面积为$\frac{1}{2}\vert k\vert$。
对于$y = -\frac{5}{x}$,$S_{\triangle AOD}=\frac{1}{2}\times\vert - 5\vert=\frac{5}{2}$;对于$y=\frac{7}{x}$,$S_{\triangle OCE}=\frac{1}{2}\times\vert7\vert=\frac{7}{2}$。
$S_{矩形ODCE}=S_{\triangle AOD}+S_{四边形ADCB}+S_{\triangle OCE}$,$S_{//ogram OABC}=S_{四边形ADCB}+S_{\triangle AOD}+S_{\triangle BEC}$,又因为$\triangle AOD\cong\triangle CBE$,所以$S_{//ogram OABC}=S_{\triangle AOD}+S_{\triangle OCE}+S_{四边形ADCB}=S_{矩形ODCE}$。
$S_{矩形ODCE}=\frac{5}{2}+\frac{7}{2}+S_{四边形ADCB}$,而$S_{//ogram OABC}=S_{\triangle AOD}+S_{\triangle BEC}+S_{四边形ADCB}$,因为$\triangle AOD\cong\triangle CBE$,所以$S_{//ogram OABC}=\frac{1}{2}\times\vert - 5\vert+\frac{1}{2}\times\vert7\vert+\frac{1}{2}\times\vert - 5\vert+\frac{1}{2}\times\vert7\vert$
$S_{//ogram OABC}=\frac{5 + 7}{2}+\frac{5 + 7}{2}=12$。
C
查看更多完整答案,请扫码查看


