《2025年快乐暑假天天练数学物理生物》

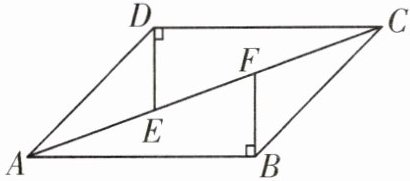
2. 如图,已知 AC 是平行四边形 ABCD 的对角线,过点 D 作 DE⊥DC,交 AC 于点 E,过点 B 作 BF⊥AB,交 AC 于点 F.
求证:CE= AF.

答案： 因为四边形$ABCD$是平行四边形，根据平行四边形的性质可知$AD = BC$，$AD// BC$，所以$\angle DAE=\angle BCF$。
又因为$DE\perp DC$，$BF\perp AB$，$AB// DC$，所以$\angle EDC=\angle FBA = 90^{\circ}$，进而可得$\angle ADE=\angle CBF$。
在$\triangle ADE$和$\triangle CBF$中，$\begin{cases}\angle DAE=\angle BCF\\AD = BC\\\angle ADE=\angle CBF\end{cases}$，根据“角 - 边 - 角”（$ASA$）全等判定定理，可得$\triangle ADE\cong\triangle CBF$。
由全等三角形的性质可知$AE = CF$。
因为$AE + EF=CF + EF$（等式的性质），所以$CE = AF$。
在平行四边形$ABCD$中，$AD = BC$，$AD// BC$，所以$\angle DAE=\angle BCF$。
因为$DE\perp DC$，$BF\perp AB$，$AB// DC$，所以$\angle EDC=\angle FBA = 90^{\circ}$，则$\angle ADE=\angle CBF$。
在$\triangle ADE$和$\triangle CBF$中，$\begin{cases}\angle DAE=\angle BCF\\AD = BC\\\angle ADE=\angle CBF\end{cases}$，所以$\triangle ADE\cong\triangle CBF(ASA)$，所以$AE = CF$。
因为$AE + EF=CF + EF$，所以$CE = AF$。
综上，$CE = AF$得证。

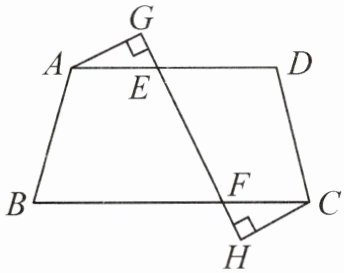
3. 如图,在四边形 ABCD 中,AD$//$BC,点 E,F 分别在 AD,BC 上,AE= CF,过点 A,C 分别作 EF 的垂线,垂足分别为 G,H.
(1)求证:$\triangle AGE\cong \triangle CHF;$
(2)连接 AC,线段 GH 与 AC 是否互相平分? 请说明理由.

答案： $(1)$ 证明$\triangle AGE\cong \triangle CHF$
已知$AG\perp EF$，$CH\perp EF$，所以$\angle AGE = \angle CHF = 90^{\circ}$。
因为$AD// BC$，根据两直线平行，内错角相等，可得$\angle AEG=\angle CFH$。
在$\triangle AGE$和$\triangle CHF$中：
$\begin{cases}\angle AGE=\angle CHF\\\angle AEG=\angle CFH\\AE = CF\end{cases}$
根据“$AAS$”（两角及其中一角的对边对应相等的两个三角形全等），可以得出$\triangle AGE\cong\triangle CHF$。
$(2)$ 判断线段$GH$与$AC$是否互相平分
连接$AH$、$CG$。
由$(1)$知$\triangle AGE\cong\triangle CHF$，所以$AG = CH$。
又因为$AG\perp EF$，$CH\perp EF$，所以$AG// CH$（垂直于同一条直线的两条直线互相平行）。
一组对边平行且相等的四边形是平行四边形，因为$AG = CH$且$AG// CH$，所以四边形$AHCG$是平行四边形。
根据平行四边形的性质：平行四边形的对角线互相平分，因为$AC$、$GH$是平行四边形$AHCG$的对角线 ，所以线段$GH$与$AC$互相平分。
$(1)$ 证明如上，可证$\triangle AGE\cong\triangle CHF(AAS)$。
$(2)$ 线段$GH$与$AC$互相平分，理由如上。