《2025年快乐暑假天天练数学物理生物》

1. 先化简$(\frac {1}{x-1}-\frac {1}{x+1})÷\frac {x}{2x^{2}-2}$的值,然后选择一个你喜欢的x的值代入求原式的值.

答案： 1. 首先化简$(\frac{1}{x - 1}-\frac{1}{x + 1})\div\frac{x}{2x^{2}-2}$：
- 对括号内的式子进行通分，$\frac{1}{x - 1}-\frac{1}{x + 1}=\frac{x + 1-(x - 1)}{(x - 1)(x + 1)}$。
- 去括号得$\frac{x + 1 - x+1}{(x - 1)(x + 1)}=\frac{2}{(x - 1)(x + 1)}$。
- 对$2x^{2}-2$进行因式分解，$2x^{2}-2 = 2(x^{2}-1)=2(x - 1)(x + 1)$。
- 则原式变为$\frac{2}{(x - 1)(x + 1)}\div\frac{x}{2(x - 1)(x + 1)}$。
- 根据除法运算法则，除以一个数等于乘以它的倒数，即$\frac{2}{(x - 1)(x + 1)}\times\frac{2(x - 1)(x + 1)}{x}$。
- 约分后得到$\frac{4}{x}$。
2. 然后确定$x$的取值范围：
- 要使原式有意义，则分母不能为$0$。
- 在$\frac{1}{x - 1}$中，$x-1\neq0$，即$x\neq1$；在$\frac{1}{x + 1}$中，$x + 1\neq0$，即$x\neq - 1$；在$\frac{x}{2x^{2}-2}$中，$2x^{2}-2\neq0$，也就是$x\neq\pm1$，且$x\neq0$。
3. 最后取值代入：
- 不妨取$x = 2$（只要满足$x\neq\pm1$且$x\neq0$即可）。
- 当$x = 2$时，$\frac{4}{x}=\frac{4}{2}=2$。
化简结果为$\frac{4}{x}$，当$x = 2$时，原式的值为$2$。

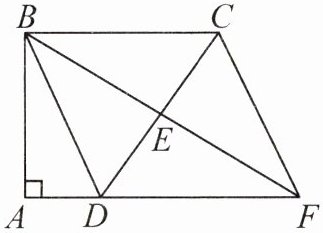
2. 如图,在四边形ABCD中,$∠A= ∠ABC= 90^{\circ }$,E是边CD的中点,连接BE并延长,求证:四边形BDFC是平行四边形.

答案： 本题可通过证明三角形全等，得到对应边相等，再结合平行四边形的判定定理进行证明。
**步骤一：证明$\triangle BEC\cong\triangle FED$**
已知$E$是边$CD$的中点，所以$CE = DE$。
因为$\angle BEC$与$\angle FED$是对顶角，根据对顶角的性质：对顶角相等，可得$\angle BEC=\angle FED$。
又因为$BC// AF$，根据两直线平行，内错角相等，可得$\angle BCE=\angle FDE$。
在$\triangle BEC$和$\triangle FED$中，$\begin{cases}\angle BEC = \angle FED\\CE = DE\\\angle BCE = \angle FDE\end{cases}$，根据“角 - 边 - 角”（$ASA$）全等判定定理，可得$\triangle BEC\cong\triangle FED$。
**步骤二：根据全等三角形的性质得到对应边相等**
根据全等三角形的性质：全等三角形的对应边相等，由$\triangle BEC\cong\triangle FED$，可得$BE = FE$。
**步骤三：根据平行四边形的判定定理证明四边形$BDFC$是平行四边形**
因为$CE = DE$，$BE = FE$，即四边形$BDFC$的对角线互相平分。
根据平行四边形的判定定理：对角线互相平分的四边形是平行四边形，所以四边形$BDFC$是平行四边形。
在$\triangle BEC$和$\triangle FED$中，
$\because E$是$CD$中点，$\therefore CE = DE$，
$\because BC// AF$，$\therefore\angle BCE=\angle FDE$，
又$\because\angle BEC=\angle FED$（对顶角相等），
$\therefore\triangle BEC\cong\triangle FED(ASA)$，
$\therefore BE = FE$，
又$\because CE = DE$，
$\therefore$四边形$BDFC$是平行四边形（对角线互相平分的四边形是平行四边形）。

3. 学校新到一批实验器材需要整理,若实验管理员李老师单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务.
(1)王师傅单独整理这批实验器材需要多少分钟完成?
(2)学校要求王师傅的工作时间不能超过30分钟,要完成整理这批器材,李老师至少要工作多少分钟?

答案： 1. 设王师傅单独整理这批实验器材需要$x$分钟完成，将工作总量看作单位“$1$”。
- 已知李老师单独整理需要$40$分钟完成，则李老师的工作效率为$\frac{1}{40}$，王师傅的工作效率为$\frac{1}{x}$。
- 根据李老师与王师傅共同整理$20$分钟，王师傅再单独整理$20$分钟完成任务，可列方程：$20\times(\frac{1}{40}+\frac{1}{x}) + 20\times\frac{1}{x}=1$。
- 去括号得：$\frac{20}{40}+\frac{20}{x}+\frac{20}{x}=1$，即$\frac{1}{2}+\frac{40}{x}=1$。
- 移项得：$\frac{40}{x}=1 - \frac{1}{2}$，$\frac{40}{x}=\frac{1}{2}$。
- 解得$x = 80$。
- 经检验，当$x = 80$时，原分式方程分母不为$0$，所以$x = 80$是原方程的解，即王师傅单独整理这批实验器材需要$80$分钟完成。
2. 设李老师要工作$y$分钟。
- 李老师的工作效率为$\frac{1}{40}$，王师傅的工作效率为$\frac{1}{80}$。
- 王师傅工作时间不能超过$30$分钟，根据工作总量为$1$，可列不等式：$\frac{1}{40}y+\frac{1}{80}\times30\geqslant1$。
- 化简不等式得：$\frac{y}{40}+\frac{30}{80}\geqslant1$，通分得到$\frac{2y}{80}+\frac{30}{80}\geqslant1$，即$\frac{2y + 30}{80}\geqslant1$。
- 两边同时乘以$80$得：$2y+30\geqslant80$。
- 移项得：$2y\geqslant80 - 30$，$2y\geqslant50$。
- 解得$y\geqslant25$。
1. 王师傅单独整理这批实验器材需要$80$分钟完成。
2. 李老师至少要工作$25$分钟。