2. 观察下列图形,图1中有3个三角形,图2中有5个三角形,图3中有7个三角形……依此规律下去,则第5个图形中三角形的个数是
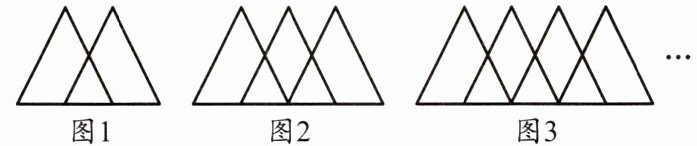
A.9个
B.11个
C.13个
D.15个
B

A.9个
B.11个
C.13个
D.15个
答案:
【解析】:
首先观察给出的图形序列,分析三角形个数的变化规律。
图1中有3个三角形,图2中有5个三角形,图3中有7个三角形。
可以看出,每个图形比前一个图形多2个三角形。
设第$n$个图形中三角形的个数为$a_n$,根据观察,可以建立如下数列:
$a_1 = 3$,
$a_2 = 5 = a_1 + 2$,
$a_3 = 7 = a_2 + 2$,
由此可以推断出这是一个等差数列,公差为2。
因此,第$n$个图形中三角形的个数可以表示为:
$a_n = a_1 + (n - 1) × 2 = 3 + (n - 1) × 2 = 2n + 1$,
将$n=5$代入上述公式,得到第5个图形中三角形的个数:
$a_5 = 2 × 5 + 1 = 11$。
【答案】:B. 11个。
首先观察给出的图形序列,分析三角形个数的变化规律。
图1中有3个三角形,图2中有5个三角形,图3中有7个三角形。
可以看出,每个图形比前一个图形多2个三角形。
设第$n$个图形中三角形的个数为$a_n$,根据观察,可以建立如下数列:
$a_1 = 3$,
$a_2 = 5 = a_1 + 2$,
$a_3 = 7 = a_2 + 2$,
由此可以推断出这是一个等差数列,公差为2。
因此,第$n$个图形中三角形的个数可以表示为:
$a_n = a_1 + (n - 1) × 2 = 3 + (n - 1) × 2 = 2n + 1$,
将$n=5$代入上述公式,得到第5个图形中三角形的个数:
$a_5 = 2 × 5 + 1 = 11$。
【答案】:B. 11个。
例 2 填空题
(1)一个等腰三角形的两边长分别是3和7,则它的周长为
(2)已知三角形的三边长分别为2,x,10,若 x 为整数,则这样的三角形个数为
(3)如图,AD 是$\triangle ABC$的边 BC 上的中线,已知$AB= 5\ \text{cm}$,$AC= 3\ \text{cm}$,则$\triangle ABD与\triangle ACD$的周长之差为
(4)如图,若 H 是$\triangle ABC$三条高 AD,BE,CF 的交点,则$\triangle HBC$中 BC 边上的高是
(1)一个等腰三角形的两边长分别是3和7,则它的周长为
17
.(2)已知三角形的三边长分别为2,x,10,若 x 为整数,则这样的三角形个数为
3
.(3)如图,AD 是$\triangle ABC$的边 BC 上的中线,已知$AB= 5\ \text{cm}$,$AC= 3\ \text{cm}$,则$\triangle ABD与\triangle ACD$的周长之差为
2
cm.(4)如图,若 H 是$\triangle ABC$三条高 AD,BE,CF 的交点,则$\triangle HBC$中 BC 边上的高是
HD
,$\triangle BHA$中 BH 边上的高是AF
.
答案:
【解析】:
(1)本题考查三角形三边关系以及等腰三角形性质。
首先,根据三角形三边关系,任意两边之和大于第三边。
对于等腰三角形,若两边长分别为3和7,需要判断哪个是腰。
若3为腰,则三边长为3,3,7,但$3 + 3 < 7$,不满足三角形三边关系。
若7为腰,则三边长为7,7,3,满足$7 + 7 > 3$且$7 + 3 > 7$,因此周长为$7 + 7 + 3 = 17$。
(2)本题考查三角形三边关系。
根据三角形三边关系,有$10 - 2 < x < 10 + 2$,即$8 < x < 12$。
由于$x$为整数,因此$x$可以取9,10,11,共有3个这样的三角形。
(3)本题考查对三角形中线的认识。
由于$AD$是$\triangle ABC$的边$BC$上的中线,根据中线的定义,$BD = CD$。
$\triangle ABD$的周长为$AB + BD + AD$,$\triangle ACD$的周长为$AC + CD + AD$。
由于$BD = CD$,且$AD$为公共边,因此$\triangle ABD$与$\triangle ACD$的周长之差为$AB - AC = 5 - 3 = 2 \text{cm}$。
(4)本题考查三角形高线的定义。
由于$H$是$\triangle ABC$三条高$AD$,$BE$,$CF$的交点,根据高线的定义,$HD$垂直于$BC$,因此$HD$是$\triangle HBC$中$BC$边上的高。
同理,$AF$垂直于$BH$的延长线,因此$AF$是$\triangle BHA$中$BH$边上的高。
【答案】:
(1)17
(2)3
(3)2
(4)$HD$;$AF$
(1)本题考查三角形三边关系以及等腰三角形性质。
首先,根据三角形三边关系,任意两边之和大于第三边。
对于等腰三角形,若两边长分别为3和7,需要判断哪个是腰。
若3为腰,则三边长为3,3,7,但$3 + 3 < 7$,不满足三角形三边关系。
若7为腰,则三边长为7,7,3,满足$7 + 7 > 3$且$7 + 3 > 7$,因此周长为$7 + 7 + 3 = 17$。
(2)本题考查三角形三边关系。
根据三角形三边关系,有$10 - 2 < x < 10 + 2$,即$8 < x < 12$。
由于$x$为整数,因此$x$可以取9,10,11,共有3个这样的三角形。
(3)本题考查对三角形中线的认识。
由于$AD$是$\triangle ABC$的边$BC$上的中线,根据中线的定义,$BD = CD$。
$\triangle ABD$的周长为$AB + BD + AD$,$\triangle ACD$的周长为$AC + CD + AD$。
由于$BD = CD$,且$AD$为公共边,因此$\triangle ABD$与$\triangle ACD$的周长之差为$AB - AC = 5 - 3 = 2 \text{cm}$。
(4)本题考查三角形高线的定义。
由于$H$是$\triangle ABC$三条高$AD$,$BE$,$CF$的交点,根据高线的定义,$HD$垂直于$BC$,因此$HD$是$\triangle HBC$中$BC$边上的高。
同理,$AF$垂直于$BH$的延长线,因此$AF$是$\triangle BHA$中$BH$边上的高。
【答案】:
(1)17
(2)3
(3)2
(4)$HD$;$AF$
3. 若一个三角形的两边长分别为3,7,则第三边的长可以是
A.3
B.4
C.7
D.10
C
A.3
B.4
C.7
D.10
答案:
【解析】:
本题主要考查三角形的三边关系,即任意两边之和大于第三边,任意两边之差小于第三边。这是三角形存在的基本条件。
已知三角形的两边长分别为3和7,设第三边长为$x$。
根据三角形的三边关系,我们可以得到以下不等式组:
$3 + 7 > x$,即 $x < 10$;
$7 - 3 < x$,即 $x > 4$。
综合以上两个不等式,我们得到第三边$x$的取值范围为:
$4 < x < 10$。
接下来,我们将选项中的数值代入这个范围进行检验:
A. $3$:不满足 $4 < x < 10$,故A选项错误;
B. $4$:不满足 $4 < x < 10$(注意等号不取),故B选项错误;
C. $7$:满足 $4 < x < 10$,故C选项正确;
D. $10$:不满足 $4 < x < 10$,故D选项错误。
【答案】:
C
本题主要考查三角形的三边关系,即任意两边之和大于第三边,任意两边之差小于第三边。这是三角形存在的基本条件。
已知三角形的两边长分别为3和7,设第三边长为$x$。
根据三角形的三边关系,我们可以得到以下不等式组:
$3 + 7 > x$,即 $x < 10$;
$7 - 3 < x$,即 $x > 4$。
综合以上两个不等式,我们得到第三边$x$的取值范围为:
$4 < x < 10$。
接下来,我们将选项中的数值代入这个范围进行检验:
A. $3$:不满足 $4 < x < 10$,故A选项错误;
B. $4$:不满足 $4 < x < 10$(注意等号不取),故B选项错误;
C. $7$:满足 $4 < x < 10$,故C选项正确;
D. $10$:不满足 $4 < x < 10$,故D选项错误。
【答案】:
C
4. 如图,$CD\perp AB$交 AB 的延长线于点 D,已知$\angle ABC$是钝角,则
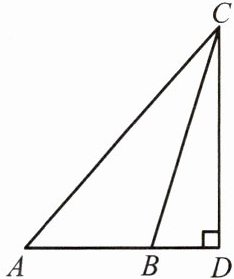
A.线段 CD 是$\triangle ABC$的 AC 边上的高线
B.线段 CD 是$\triangle ABC$的 AB 边上的高线
C.线段 AD 是$\triangle ABC$的 BC 边上的高线
D.线段 AD 是$\triangle ABC$的 AC 边上的高线
B

A.线段 CD 是$\triangle ABC$的 AC 边上的高线
B.线段 CD 是$\triangle ABC$的 AB 边上的高线
C.线段 AD 是$\triangle ABC$的 BC 边上的高线
D.线段 AD 是$\triangle ABC$的 AC 边上的高线
答案:
【解析】:本题考查了三角形高线的定义。
三角形的高线是从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段。
在本题中,$CD\perp AB$,即线段$CD$是从$\triangle ABC$的顶点$C$向对边$AB$(或$AB$的延长线)作的垂线,所以线段$CD$是$\triangle ABC$的$AB$边上的高线。
A选项,线段$CD$不是$\triangle ABC$的$AC$边上的高线,因为$AC$边上的高线应该是从$B$点向$AC$作垂线,故A错误。
C选项,线段$AD$不是$\triangle ABC$的$BC$边上的高线,因为$BC$边上的高线应该是从$A$点向$BC$作垂线,故C错误。
D选项,线段$AD$不是$\triangle ABC$的$AC$边上的高线,因为$AC$边上的高线应该是从$B$点向$AC$作垂线,故D错误。
【答案】:B
三角形的高线是从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段。
在本题中,$CD\perp AB$,即线段$CD$是从$\triangle ABC$的顶点$C$向对边$AB$(或$AB$的延长线)作的垂线,所以线段$CD$是$\triangle ABC$的$AB$边上的高线。
A选项,线段$CD$不是$\triangle ABC$的$AC$边上的高线,因为$AC$边上的高线应该是从$B$点向$AC$作垂线,故A错误。
C选项,线段$AD$不是$\triangle ABC$的$BC$边上的高线,因为$BC$边上的高线应该是从$A$点向$BC$作垂线,故C错误。
D选项,线段$AD$不是$\triangle ABC$的$AC$边上的高线,因为$AC$边上的高线应该是从$B$点向$AC$作垂线,故D错误。
【答案】:B
例 3 如图,BD 是$\triangle ABC$的角平分线,$ED// BC$交 AB 于点 E.
(1)若$\angle A= 44^\circ$,$\angle3= 60^\circ$,求$\angle BED$的度数;
(2)若$\angle A-\angle2= 31^\circ$,$\angle EDC= 76^\circ$,求$\angle ADB$的度数.
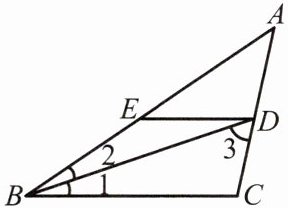
(1)若$\angle A= 44^\circ$,$\angle3= 60^\circ$,求$\angle BED$的度数;
(2)若$\angle A-\angle2= 31^\circ$,$\angle EDC= 76^\circ$,求$\angle ADB$的度数.

答案:
(1)解:
∵BD是△ABC的角平分线
∴∠1=∠2
∵ED//BC
∴∠2=∠1(两直线平行,内错角相等),∠AED=∠ABC,∠ADE=∠C=∠3=60°
在△AED中,∠A=44°,∠ADE=60°
∴∠AED=180°-∠A-∠ADE=180°-44°-60°=76°
∴∠ABC=∠AED=76°
∵∠1=∠2,∠ABC=∠1+∠2=76°
∴∠2=38°
∵∠BED+∠AED=180°
∴∠BED=180°-∠AED=180°-76°=104°
(2)解:
∵ED//BC
∴∠EDC+∠C=180°(两直线平行,同旁内角互补)
∵∠EDC=76°
∴∠C=180°-∠EDC=180°-76°=104°=∠3
∵∠A-∠2=31°
∴∠A=∠2+31°
∵BD是△ABC的角平分线
∴∠1=∠2
在△ABC中,∠A+∠ABC+∠C=180°
∠ABC=∠1+∠2=2∠2
∴∠2+31°+2∠2+104°=180°
3∠2=45°
∠2=15°
∴∠A=15°+31°=46°
在△ABD中,∠A+∠2+∠ADB=180°
∴∠ADB=180°-∠A-∠2=180°-46°-15°=119°
(1)解:
∵BD是△ABC的角平分线
∴∠1=∠2
∵ED//BC
∴∠2=∠1(两直线平行,内错角相等),∠AED=∠ABC,∠ADE=∠C=∠3=60°
在△AED中,∠A=44°,∠ADE=60°
∴∠AED=180°-∠A-∠ADE=180°-44°-60°=76°
∴∠ABC=∠AED=76°
∵∠1=∠2,∠ABC=∠1+∠2=76°
∴∠2=38°
∵∠BED+∠AED=180°
∴∠BED=180°-∠AED=180°-76°=104°
(2)解:
∵ED//BC
∴∠EDC+∠C=180°(两直线平行,同旁内角互补)
∵∠EDC=76°
∴∠C=180°-∠EDC=180°-76°=104°=∠3
∵∠A-∠2=31°
∴∠A=∠2+31°
∵BD是△ABC的角平分线
∴∠1=∠2
在△ABC中,∠A+∠ABC+∠C=180°
∠ABC=∠1+∠2=2∠2
∴∠2+31°+2∠2+104°=180°
3∠2=45°
∠2=15°
∴∠A=15°+31°=46°
在△ABD中,∠A+∠2+∠ADB=180°
∴∠ADB=180°-∠A-∠2=180°-46°-15°=119°
5. 如图,在$\triangle ABC$中,$\angle ABC$,$\angle ACB$的平分线 BE,CD 相交于点 F,$\angle ABC= 42^\circ$,$\angle A= 60^\circ$,则$\angle BFC$的度数为(
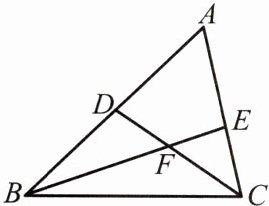
A.$118^\circ$
B.$119^\circ$
C.$120^\circ$
D.$121^\circ$
C
)
A.$118^\circ$
B.$119^\circ$
C.$120^\circ$
D.$121^\circ$
答案:
【解析】:本题可根据三角形内角和定理求出$\angle ACB$的度数,再利用角平分线的性质求出$\angle FBC$与$\angle FCB$的度数和,最后根据三角形内角和定理求出$\angle BFC$的度数。
步骤一:求$\angle ACB$的度数
在$\triangle ABC$中,已知$\angle A = 60^{\circ}$,$\angle ABC = 42^{\circ}$,根据三角形内角和定理:三角形内角和为$180^{\circ}$,可得$\angle ACB$的度数为:
$\angle ACB=180^{\circ}-\angle A - \angle ABC=180^{\circ}-60^{\circ}-42^{\circ}=78^{\circ}$
步骤二:求$\angle FBC$与$\angle FCB$的度数和
因为$BE$平分$\angle ABC$,$CD$平分$\angle ACB$,所以$\angle FBC=\frac{1}{2}\angle ABC$,$\angle FCB=\frac{1}{2}\angle ACB$。
则$\angle FBC + \angle FCB=\frac{1}{2}(\angle ABC + \angle ACB)=\frac{1}{2}×(42^{\circ}+78^{\circ})=\frac{1}{2}×120^{\circ}=60^{\circ}$。
步骤三:求$\angle BFC$的度数
在$\triangle BFC$中,根据三角形内角和定理,可得$\angle BFC$的度数为:
$\angle BFC=180^{\circ}-(\angle FBC + \angle FCB)=180^{\circ}-60^{\circ}=120^{\circ}$
【答案】:C
步骤一:求$\angle ACB$的度数
在$\triangle ABC$中,已知$\angle A = 60^{\circ}$,$\angle ABC = 42^{\circ}$,根据三角形内角和定理:三角形内角和为$180^{\circ}$,可得$\angle ACB$的度数为:
$\angle ACB=180^{\circ}-\angle A - \angle ABC=180^{\circ}-60^{\circ}-42^{\circ}=78^{\circ}$
步骤二:求$\angle FBC$与$\angle FCB$的度数和
因为$BE$平分$\angle ABC$,$CD$平分$\angle ACB$,所以$\angle FBC=\frac{1}{2}\angle ABC$,$\angle FCB=\frac{1}{2}\angle ACB$。
则$\angle FBC + \angle FCB=\frac{1}{2}(\angle ABC + \angle ACB)=\frac{1}{2}×(42^{\circ}+78^{\circ})=\frac{1}{2}×120^{\circ}=60^{\circ}$。
步骤三:求$\angle BFC$的度数
在$\triangle BFC$中,根据三角形内角和定理,可得$\angle BFC$的度数为:
$\angle BFC=180^{\circ}-(\angle FBC + \angle FCB)=180^{\circ}-60^{\circ}=120^{\circ}$
【答案】:C
6. 在$\triangle ABC$中,$\angle A比它相邻的外角小10^\circ$,则$\angle B+\angle C$为
A.$85^\circ$
B.$95^\circ$
C.$100^\circ$
D.$110^\circ$
B
A.$85^\circ$
B.$95^\circ$
C.$100^\circ$
D.$110^\circ$
答案:
解:设∠A的度数为x,则与∠A相邻的外角的度数为x+10°。
因为∠A与它相邻的外角互补,所以x + (x + 10°) = 180°,
解得x = 85°,即∠A = 85°。
在△ABC中,∠B + ∠C = 180° - ∠A = 180° - 85° = 95°。
答案:B
因为∠A与它相邻的外角互补,所以x + (x + 10°) = 180°,
解得x = 85°,即∠A = 85°。
在△ABC中,∠B + ∠C = 180° - ∠A = 180° - 85° = 95°。
答案:B
7. 具备下列条件的四个三角形中,不是直角三角形的是
A.$\angle A= \angle B= \frac{1}{2}\angle C$
B.$\angle A-\angle B= 90^\circ$
C.$\angle A+\angle B= \angle C$
D.$\angle A= 90^\circ-\angle B$
B
A.$\angle A= \angle B= \frac{1}{2}\angle C$
B.$\angle A-\angle B= 90^\circ$
C.$\angle A+\angle B= \angle C$
D.$\angle A= 90^\circ-\angle B$
答案:
【解析】:
本题主要考察三角形的内角和定理以及直角三角形的性质。
A选项:由给定条件 $\angle A = \angle B = \frac{1}{2}\angle C$,设 $\angle A = x$,则 $\angle B = x$,$\angle C = 2x$。根据三角形内角和为$180^\circ$,有 $x + x + 2x = 180^\circ$,解得 $x = 45^\circ$,$\angle C = 90^\circ$。因此,这是一个直角三角形,不符合题意。
B选项:由给定条件 $\angle A - \angle B = 90^\circ$,移项得 $\angle A = \angle B + 90^\circ$。代入三角形内角和公式 $\angle A + \angle B + \angle C = 180^\circ$,得 $\angle B + 90^\circ + \angle B + \angle C = 180^\circ$,即 $2\angle B + \angle C = 90^\circ$。由于 $\angle B$ 和 $\angle C$ 都必须是正数,因此 $\angle A$ 必然大于 $90^\circ$,这意味着三角形不是直角三角形,符合题意。
C选项:由给定条件 $\angle A + \angle B = \angle C$,结合三角形内角和公式,得 $2\angle C = 180^\circ$,解得 $\angle C = 90^\circ$。因此,这是一个直角三角形,不符合题意。
D选项:由给定条件 $\angle A = 90^\circ - \angle B$,移项并结合三角形内角和公式,可以推出 $\angle C = 90^\circ$。因此,这也是一个直角三角形,不符合题意。
综上所述,只有B选项的三角形不是直角三角形。
【答案】:
B
本题主要考察三角形的内角和定理以及直角三角形的性质。
A选项:由给定条件 $\angle A = \angle B = \frac{1}{2}\angle C$,设 $\angle A = x$,则 $\angle B = x$,$\angle C = 2x$。根据三角形内角和为$180^\circ$,有 $x + x + 2x = 180^\circ$,解得 $x = 45^\circ$,$\angle C = 90^\circ$。因此,这是一个直角三角形,不符合题意。
B选项:由给定条件 $\angle A - \angle B = 90^\circ$,移项得 $\angle A = \angle B + 90^\circ$。代入三角形内角和公式 $\angle A + \angle B + \angle C = 180^\circ$,得 $\angle B + 90^\circ + \angle B + \angle C = 180^\circ$,即 $2\angle B + \angle C = 90^\circ$。由于 $\angle B$ 和 $\angle C$ 都必须是正数,因此 $\angle A$ 必然大于 $90^\circ$,这意味着三角形不是直角三角形,符合题意。
C选项:由给定条件 $\angle A + \angle B = \angle C$,结合三角形内角和公式,得 $2\angle C = 180^\circ$,解得 $\angle C = 90^\circ$。因此,这是一个直角三角形,不符合题意。
D选项:由给定条件 $\angle A = 90^\circ - \angle B$,移项并结合三角形内角和公式,可以推出 $\angle C = 90^\circ$。因此,这也是一个直角三角形,不符合题意。
综上所述,只有B选项的三角形不是直角三角形。
【答案】:
B
查看更多完整答案,请扫码查看


