4. 如图,某小区花坛的形状是左右对称的六边形ABCDEF,若∠AFC+∠DCF= 150°,则∠E+∠D的度数为 (
A.200°
B.210°
C.230°
D.250°
B
)A.200°
B.210°
C.230°
D.250°
答案:
【解析】:本题可根据轴对称图形的性质以及多边形内角和定理来求解$\angle E + \angle D$的度数。
步骤一:分析六边形$ABCDEF$的性质
已知六边形$ABCDEF$是左右对称的轴对称图形,根据轴对称图形的性质可知,对称轴两侧的对应角相等,即$\angle A=\angle D$,$\angle B=\angle E$,$\angle AFC=\angle EFC$,$\angle DCF=\angle BCF$。
步骤二:求出$\angle BCF + \angle EFC$的度数
已知$\angle AFC + \angle DCF = 150^{\circ}$,因为$\angle AFC=\angle EFC$,$\angle DCF=\angle BCF$,所以$\angle BCF + \angle EFC = \angle AFC + \angle DCF = 150^{\circ}$。
步骤三:利用多边形内角和定理求出$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F$的度数
根据多边形内角和定理:$n$边形内角和为$(n - 2)×180^{\circ}$($n\geqslant 3$且$n$为整数),对于六边形$ABCDEF$,$n = 6$,则其内角和为$(6 - 2)×180^{\circ}= 720^{\circ}$,即$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F = 720^{\circ}$。
步骤四:求出$\angle A + \angle B + \angle D + \angle E$的度数
因为$\angle C = \angle BCF + \angle DCF$,$\angle F = \angle AFC + \angle EFC$,且$\angle BCF + \angle EFC = 150^{\circ}$,$\angle AFC + \angle DCF = 150^{\circ}$,所以$\angle C + \angle F = 150^{\circ}+150^{\circ}= 300^{\circ}$。
将$\angle C + \angle F = 300^{\circ}$代入$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F = 720^{\circ}$,可得$\angle A + \angle B + \angle D + \angle E = 720^{\circ}- 300^{\circ}= 420^{\circ}$。
步骤五:求出$\angle E + \angle D$的度数
由$\angle A=\angle D$,$\angle B=\angle E$,可得$2(\angle E + \angle D)= 420^{\circ}$,则$\angle E + \angle D = 210^{\circ}$。
【答案】:B
步骤一:分析六边形$ABCDEF$的性质
已知六边形$ABCDEF$是左右对称的轴对称图形,根据轴对称图形的性质可知,对称轴两侧的对应角相等,即$\angle A=\angle D$,$\angle B=\angle E$,$\angle AFC=\angle EFC$,$\angle DCF=\angle BCF$。
步骤二:求出$\angle BCF + \angle EFC$的度数
已知$\angle AFC + \angle DCF = 150^{\circ}$,因为$\angle AFC=\angle EFC$,$\angle DCF=\angle BCF$,所以$\angle BCF + \angle EFC = \angle AFC + \angle DCF = 150^{\circ}$。
步骤三:利用多边形内角和定理求出$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F$的度数
根据多边形内角和定理:$n$边形内角和为$(n - 2)×180^{\circ}$($n\geqslant 3$且$n$为整数),对于六边形$ABCDEF$,$n = 6$,则其内角和为$(6 - 2)×180^{\circ}= 720^{\circ}$,即$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F = 720^{\circ}$。
步骤四:求出$\angle A + \angle B + \angle D + \angle E$的度数
因为$\angle C = \angle BCF + \angle DCF$,$\angle F = \angle AFC + \angle EFC$,且$\angle BCF + \angle EFC = 150^{\circ}$,$\angle AFC + \angle DCF = 150^{\circ}$,所以$\angle C + \angle F = 150^{\circ}+150^{\circ}= 300^{\circ}$。
将$\angle C + \angle F = 300^{\circ}$代入$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F = 720^{\circ}$,可得$\angle A + \angle B + \angle D + \angle E = 720^{\circ}- 300^{\circ}= 420^{\circ}$。
步骤五:求出$\angle E + \angle D$的度数
由$\angle A=\angle D$,$\angle B=\angle E$,可得$2(\angle E + \angle D)= 420^{\circ}$,则$\angle E + \angle D = 210^{\circ}$。
【答案】:B
5. 如图,直线l是四边形ABCD的对称轴,若线段AC= 8cm,线段BD= 6cm,则阴影部分的面积为$
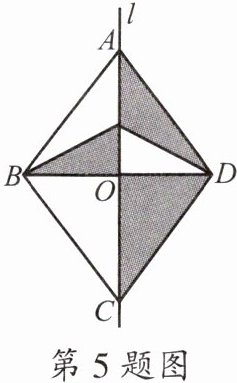
12
cm^2.$
答案:
【解析】:本题可根据轴对称的性质,得出阴影部分面积与四边形面积的关系,进而求出阴影部分的面积。
步骤一:分析轴对称的性质
已知直线$l$是四边形$ABCD$的对称轴,根据轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,且这两个图形全等。
所以四边形$ABCD$沿直线$l$对折后,直线$l$两侧的图形能够完全重合,即四边形$ABCD$被直线$l$分成的两部分面积相等。
步骤二:确定阴影部分面积与四边形面积的关系
观察图形可知,阴影部分是四边形$ABCD$的一半,所以阴影部分的面积等于四边形$ABCD$面积的一半。
步骤三:计算四边形$ABCD$的面积
因为直线$l$是四边形$ABCD$的对称轴,$AC$、$BD$相交于点$O$,根据轴对称的性质可知$AC$被直线$l$垂直平分,$BD$也被直线$l$垂直平分,且$AC\perp BD$(对称轴与对应点所连线段垂直)。
此时四边形$ABCD$的面积可以看作是四个直角三角形的面积之和,这四个直角三角形两两全等。
以$\triangle AOB$、$\triangle BOC$、$\triangle COD$、$\triangle DOA$为例,$AC = 8cm$,则$AO=OC=\frac{1}{2}AC = \frac{1}{2}×8 = 4cm$;$BD = 6cm$,则$BO = OD=\frac{1}{2}BD=\frac{1}{2}×6 = 3cm$。
根据三角形面积公式$S=\frac{1}{2}ah$(其中$a$为底,$h$为高),可得$\triangle AOB$的面积为$\frac{1}{2}× AO× BO=\frac{1}{2}×4×3 = 6cm^2$。
那么四边形$ABCD$的面积为$4×\triangle AOB$的面积,即$4×6 = 24cm^2$。
步骤四:计算阴影部分的面积
因为阴影部分的面积等于四边形$ABCD$面积的一半,所以阴影部分的面积为$\frac{1}{2}×24 = 12cm^2$。
【答案】:$12$
步骤一:分析轴对称的性质
已知直线$l$是四边形$ABCD$的对称轴,根据轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,且这两个图形全等。
所以四边形$ABCD$沿直线$l$对折后,直线$l$两侧的图形能够完全重合,即四边形$ABCD$被直线$l$分成的两部分面积相等。
步骤二:确定阴影部分面积与四边形面积的关系
观察图形可知,阴影部分是四边形$ABCD$的一半,所以阴影部分的面积等于四边形$ABCD$面积的一半。
步骤三:计算四边形$ABCD$的面积
因为直线$l$是四边形$ABCD$的对称轴,$AC$、$BD$相交于点$O$,根据轴对称的性质可知$AC$被直线$l$垂直平分,$BD$也被直线$l$垂直平分,且$AC\perp BD$(对称轴与对应点所连线段垂直)。
此时四边形$ABCD$的面积可以看作是四个直角三角形的面积之和,这四个直角三角形两两全等。
以$\triangle AOB$、$\triangle BOC$、$\triangle COD$、$\triangle DOA$为例,$AC = 8cm$,则$AO=OC=\frac{1}{2}AC = \frac{1}{2}×8 = 4cm$;$BD = 6cm$,则$BO = OD=\frac{1}{2}BD=\frac{1}{2}×6 = 3cm$。
根据三角形面积公式$S=\frac{1}{2}ah$(其中$a$为底,$h$为高),可得$\triangle AOB$的面积为$\frac{1}{2}× AO× BO=\frac{1}{2}×4×3 = 6cm^2$。
那么四边形$ABCD$的面积为$4×\triangle AOB$的面积,即$4×6 = 24cm^2$。
步骤四:计算阴影部分的面积
因为阴影部分的面积等于四边形$ABCD$面积的一半,所以阴影部分的面积为$\frac{1}{2}×24 = 12cm^2$。
【答案】:$12$
例 3 如图,△ABC和△A'B'C'关于直线MN对称,点A',B',C'分别是点A,B,C的对称点,线段AA',BB',CC'与直线MN有什么关系?
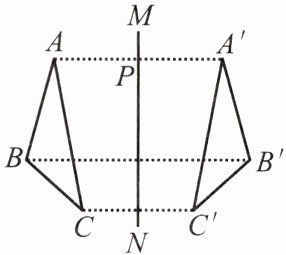
归纳:
轴对称的性质:
(1)成轴对称的两个图形是全等图形;
(2)轴对称图形的对称轴,是其任意一对对称点所连线段的垂直平分线;
(3)轴对称图形的对应线段(如AC和A'C')的交点(或其延长线的交点)必在对称轴上.

归纳:
轴对称的性质:
(1)成轴对称的两个图形是全等图形;
(2)轴对称图形的对称轴,是其任意一对对称点所连线段的垂直平分线;
(3)轴对称图形的对应线段(如AC和A'C')的交点(或其延长线的交点)必在对称轴上.
答案:
【解析】:本题主要考查轴对称的性质。
根据轴对称的性质,如果两个图形关于某条直线对称,那么这条直线就是这两个图形对称点所连线段的垂直平分线。
在本题中,$\bigtriangleup ABC$和$\bigtriangleup A'B'C'$关于直线$MN$对称,点$A'$,$B'$,$C'$分别是点$A$,$B$,$C$的对称点。
对于线段$AA'$,由于$A$和$A'$是关于直线$MN$的对称点,根据轴对称的性质,直线$MN$就是线段$AA'$的垂直平分线。
同理,对于线段$BB'$和$CC'$,由于$B$和$B'$,$C$和$C'$也是关于直线$MN$的对称点,所以直线$MN$也是线段$BB'$和$CC'$的垂直平分线。
【答案】:线段$AA'$,$BB'$,$CC'$与直线$MN$的关系是:直线$MN$垂直平分线段$AA'$,$BB'$,$CC'$。
根据轴对称的性质,如果两个图形关于某条直线对称,那么这条直线就是这两个图形对称点所连线段的垂直平分线。
在本题中,$\bigtriangleup ABC$和$\bigtriangleup A'B'C'$关于直线$MN$对称,点$A'$,$B'$,$C'$分别是点$A$,$B$,$C$的对称点。
对于线段$AA'$,由于$A$和$A'$是关于直线$MN$的对称点,根据轴对称的性质,直线$MN$就是线段$AA'$的垂直平分线。
同理,对于线段$BB'$和$CC'$,由于$B$和$B'$,$C$和$C'$也是关于直线$MN$的对称点,所以直线$MN$也是线段$BB'$和$CC'$的垂直平分线。
【答案】:线段$AA'$,$BB'$,$CC'$与直线$MN$的关系是:直线$MN$垂直平分线段$AA'$,$BB'$,$CC'$。
6. 如图,直线a是五边形ABCDE的对称轴,根据轴对称的性质可知:
(1)线段AB的对应线段是
(2)点C的对应点是
(3)∠ABC的对应角是
(4)连接BE,则线段BE被直线a
(1)线段AB的对应线段是
AE
;(2)点C的对应点是
D
;(3)∠ABC的对应角是
∠AED
;(4)连接BE,则线段BE被直线a
垂直平分
.
答案:
【解析】:
题目考查轴对称图形的性质,即如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,对应线段相等,对应角相等。
(1)观察图形可知,线段$AB$与线段$AE$关于直线$a$对称,所以线段$AB$的对应线段是$AE$。
(2)点$C$与点$D$关于直线$a$对称,所以点$C$的对应点是$D$。
(3)根据轴对称的性质,对应角相等,$\angle ABC$与$\angle AED$关于直线$a$对称,所以$\angle ABC$的对应角是$\angle AED$。
(4)因为直线$a$是五边形$ABCDE$的对称轴,$B$与$E$关于直线$a$对称,所以连接$BE$,线段$BE$被直线$a$垂直平分。
【答案】:
(1)$AE$;
(2)$D$;
(3)$\angle AED$;
(4)垂直平分。
题目考查轴对称图形的性质,即如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,对应线段相等,对应角相等。
(1)观察图形可知,线段$AB$与线段$AE$关于直线$a$对称,所以线段$AB$的对应线段是$AE$。
(2)点$C$与点$D$关于直线$a$对称,所以点$C$的对应点是$D$。
(3)根据轴对称的性质,对应角相等,$\angle ABC$与$\angle AED$关于直线$a$对称,所以$\angle ABC$的对应角是$\angle AED$。
(4)因为直线$a$是五边形$ABCDE$的对称轴,$B$与$E$关于直线$a$对称,所以连接$BE$,线段$BE$被直线$a$垂直平分。
【答案】:
(1)$AE$;
(2)$D$;
(3)$\angle AED$;
(4)垂直平分。
7. 如图,直线l是四边形ABCD的对称轴,且AB= CD,有下面的结论:①AB⊥BC;②AC⊥BD;③AB//CD;④AO= CO.其中正确的结论有______.(填序号)
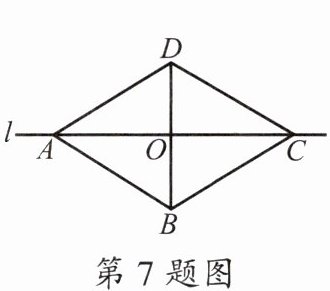

②③④
答案:
解:
∵直线l是四边形ABCD的对称轴,
∴AD=AB,CD=CB,∠DAO=∠BAO,∠DCO=∠BCO,
∵AB=CD,
∴AD=AB=CB=CD,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,∠DCA=∠BCA,
∵∠DAO=∠BAO,∠DCO=∠BCO,
∴∠DAO=∠BAO=∠DCO=∠BCO,
∵AD=CD,∠DAO=∠DCO,∠AOD=∠COB,
∴△AOD≌△COB(AAS),
∴AO=CO,④正确;
∵AD=AB,AO=AO,∠DAO=∠BAO,
∴△ADO≌△ABO(SAS),
∴∠AOD=∠AOB,
∵∠AOD+∠AOB=180°,
∴∠AOD=∠AOB=90°,
∴AC⊥BD,②正确;
∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形,
∴AB//CD,③正确;
无法得出AB⊥BC,①错误。
正确的结论有②③④。
答案:②③④
∵直线l是四边形ABCD的对称轴,
∴AD=AB,CD=CB,∠DAO=∠BAO,∠DCO=∠BCO,
∵AB=CD,
∴AD=AB=CB=CD,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,∠DCA=∠BCA,
∵∠DAO=∠BAO,∠DCO=∠BCO,
∴∠DAO=∠BAO=∠DCO=∠BCO,
∵AD=CD,∠DAO=∠DCO,∠AOD=∠COB,
∴△AOD≌△COB(AAS),
∴AO=CO,④正确;
∵AD=AB,AO=AO,∠DAO=∠BAO,
∴△ADO≌△ABO(SAS),
∴∠AOD=∠AOB,
∵∠AOD+∠AOB=180°,
∴∠AOD=∠AOB=90°,
∴AC⊥BD,②正确;
∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形,
∴AB//CD,③正确;
无法得出AB⊥BC,①错误。
正确的结论有②③④。
答案:②③④
1. 垂直平分线的性质定理:线段垂直平分线上的点与这条线段两个端点的距离
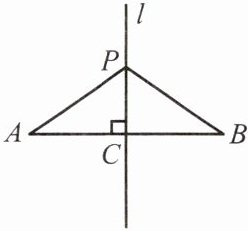
符号语言:
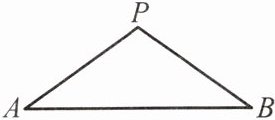
如图,$\because$ 直线$l\perp AB$,垂足为$C$,$AC= CB$,点$P在l$上,$\therefore PA= PB$.
相等
.
符号语言:
如图,$\because$ 直线$l\perp AB$,垂足为$C$,$AC= CB$,点$P在l$上,$\therefore PA= PB$.
答案:
【解析】:本题主要考查线段垂直平分线的性质定理。
线段垂直平分线的性质定理为:线段垂直平分线上的点与这条线段两个端点的距离相等。
在本题的图中,直线$l$垂直平分线段$AB$,垂足为$C$,且$AC = CB$,点$P$在直线$l$上,根据上述性质定理,就可以得出$PA = PB$。
【答案】:相等
线段垂直平分线的性质定理为:线段垂直平分线上的点与这条线段两个端点的距离相等。
在本题的图中,直线$l$垂直平分线段$AB$,垂足为$C$,且$AC = CB$,点$P$在直线$l$上,根据上述性质定理,就可以得出$PA = PB$。
【答案】:相等
2. 垂直平分线的判定定理:与线段两个端点距离相等的点在这条线段的
符号语言:
如图,$\because PA= PB$,
$\therefore$ 点$P在AB$的垂直平分线上.
注意:
线段的垂直平分线可以看成与$A,B$两点的距离相等的点的集合.
垂直平分线
上.符号语言:
如图,$\because PA= PB$,
$\therefore$ 点$P在AB$的垂直平分线上.

注意:
线段的垂直平分线可以看成与$A,B$两点的距离相等的点的集合.
答案:
【解析】:本题考查线段的垂直平分线的判定定理,该定理说明与一条线段的两个端点距离相等的点位于这条线段的垂直平分线上。
【答案】:垂直平分线。
【答案】:垂直平分线。
3. 如果两个命题的题设与结论正好相反,那么我们把这两个命题叫作
注:一般地,原命题成立时,它的逆命题可能成立,也可能不成立.
互为逆命题
. 如果把其中一个叫作原命题,那么另一个命题叫作它的逆命题
.注:一般地,原命题成立时,它的逆命题可能成立,也可能不成立.
答案:
【解析】:本题主要考察了命题及其关系,特别是原命题与逆命题的定义。根据命题的定义,一个命题由题设和结论两部分组成。当两个命题的题设与结论正好相反时,这两个命题被称为互为逆命题。
【答案】:互为逆命题;逆命题。
【答案】:互为逆命题;逆命题。
4. 如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作
互逆定理
. 其中一个定理叫作另一个定理的逆定理
.
答案:
【解析】:
本题考查的是对定理与逆定理,以及互逆定理的理解。在数学中,如果一个定理的逆命题也是真命题,那么这两个定理具有特殊的关系,它们被称为互逆定理。其中一个定理可以被称为另一个定理的逆定理。
【答案】:
互逆定理;逆定理。
本题考查的是对定理与逆定理,以及互逆定理的理解。在数学中,如果一个定理的逆命题也是真命题,那么这两个定理具有特殊的关系,它们被称为互逆定理。其中一个定理可以被称为另一个定理的逆定理。
【答案】:
互逆定理;逆定理。
例1 选择题
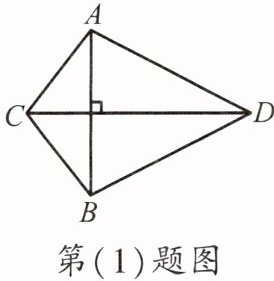
(1)如图,$CD是线段AB$的垂直平分线,若$AC= 1.6\,\text{cm}$,$BD= 2.3\,\text{cm}$,则四边形$ACBD$的周长为(
A.$3.9\,\text{cm}$ B.$7.8\,\text{cm}$ C.$4\,\text{cm}$ D.$4.6\,\text{cm}$
(2)如图,在$\triangle ABC$中,$AC的垂直平分线ED交AC于点E$,交$AB于点D$,$CE= 4$,$\triangle BCD$的周长是12,则$\triangle ABC$的周长为(
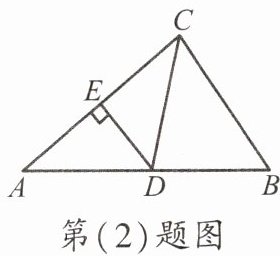
A.20 B.18 C.16 D.14
分析:利用垂直平分线性质的关键是找到垂直平分线上的点,由该点到线段两端点距离相等来进行等量关系的转化,易得(1)小题中$AC= BC$,$AD= BD$,从而得四边形$ACBD$的周长;(2)小题中$AE= CE$,$DC= AD$,从而易得$\triangle ABC$的周长.
(1)如图,$CD是线段AB$的垂直平分线,若$AC= 1.6\,\text{cm}$,$BD= 2.3\,\text{cm}$,则四边形$ACBD$的周长为(
B
)A.$3.9\,\text{cm}$ B.$7.8\,\text{cm}$ C.$4\,\text{cm}$ D.$4.6\,\text{cm}$
(2)如图,在$\triangle ABC$中,$AC的垂直平分线ED交AC于点E$,交$AB于点D$,$CE= 4$,$\triangle BCD$的周长是12,则$\triangle ABC$的周长为(
A
)

A.20 B.18 C.16 D.14
分析:利用垂直平分线性质的关键是找到垂直平分线上的点,由该点到线段两端点距离相等来进行等量关系的转化,易得(1)小题中$AC= BC$,$AD= BD$,从而得四边形$ACBD$的周长;(2)小题中$AE= CE$,$DC= AD$,从而易得$\triangle ABC$的周长.
答案:
(1)解:
∵CD是线段AB的垂直平分线,
∴AC=BC=1.6cm,AD=BD=2.3cm,
∴四边形ACBD的周长=AC+BC+BD+AD=1.6+1.6+2.3+2.3=7.8cm,
故选B。
(2)解:
∵ED是AC的垂直平分线,CE=4,
∴AC=2CE=8,AD=DC,
∵△BCD的周长是12,即BC+CD+BD=12,
∴BC+AD+BD=BC+AB=12,
∴△ABC的周长=AB+BC+AC=12+8=20,
故选A。
(1)解:
∵CD是线段AB的垂直平分线,
∴AC=BC=1.6cm,AD=BD=2.3cm,
∴四边形ACBD的周长=AC+BC+BD+AD=1.6+1.6+2.3+2.3=7.8cm,
故选B。
(2)解:
∵ED是AC的垂直平分线,CE=4,
∴AC=2CE=8,AD=DC,
∵△BCD的周长是12,即BC+CD+BD=12,
∴BC+AD+BD=BC+AB=12,
∴△ABC的周长=AB+BC+AC=12+8=20,
故选A。
查看更多完整答案,请扫码查看


