4.如图,CD是$\triangle ABC$的中线,DE是$\triangle ACD$的中线,EF是$\triangle ADE$的中线.若$\triangle AEF的面积是1\ \text{cm}^2$,则$\triangle ABC$的面积为
8
$\text{cm}^2$.
答案:
解:
∵EF是△ADE的中线,
∴S△ADE=2S△AEF=2×1=2 cm2.
∵DE是△ACD的中线,
∴S△ACD=2S△ADE=2×2=4 cm2.
∵CD是△ABC的中线,
∴S△ABC=2S△ACD=2×4=8 cm2.
8
∵EF是△ADE的中线,
∴S△ADE=2S△AEF=2×1=2 cm2.
∵DE是△ACD的中线,
∴S△ACD=2S△ADE=2×2=4 cm2.
∵CD是△ABC的中线,
∴S△ABC=2S△ACD=2×4=8 cm2.
8
5.如图,AD,CE都是$\triangle ABC$的中线,连接ED,$\triangle ABC的面积是10\ \text{cm}^2$,则$\triangle BDE$的面积是 (
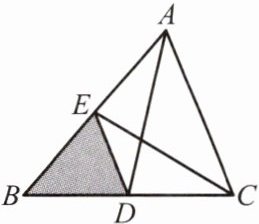
A.$1.25\ \text{cm}^2$
B.$2\ \text{cm}^2$
C.$2.5\ \text{cm}^2$
D.$5\ \text{cm}^2$
C
)
A.$1.25\ \text{cm}^2$
B.$2\ \text{cm}^2$
C.$2.5\ \text{cm}^2$
D.$5\ \text{cm}^2$
答案:
解:
∵AD是△ABC的中线,
∴BD=DC,
∴S△ABD=S△ADC=1/2S△ABC=5cm²。
∵CE是△ABC的中线,
∴AE=EB,
∴S△BEC=1/2S△ABC=5cm²。
∵ED是△BEC的中线(D为BC中点),
∴S△BDE=1/2S△BEC=2.5cm²。
答案:C
∵AD是△ABC的中线,
∴BD=DC,
∴S△ABD=S△ADC=1/2S△ABC=5cm²。
∵CE是△ABC的中线,
∴AE=EB,
∴S△BEC=1/2S△ABC=5cm²。
∵ED是△BEC的中线(D为BC中点),
∴S△BDE=1/2S△BEC=2.5cm²。
答案:C
1.三角形的内角和定理:三角形的内角和等于
符号语言:
在△ABC中,
∠A+∠B+∠C= 180°.

$180^{\circ}$
.符号语言:
在△ABC中,
∠A+∠B+∠C= 180°.

答案:
【解析】:
本题考查三角形内角和定理的内容及表示方式。三角形内角和定理是三角形的基本性质,即三角形的三个内角之和等于一个固定值。在符号语言中,我们通常使用角度的符号(如∠A、∠B、∠C)来表示三角形的各个内角,并使用等式来表示它们之间的关系。
【答案】:
$180^{\circ}$
本题考查三角形内角和定理的内容及表示方式。三角形内角和定理是三角形的基本性质,即三角形的三个内角之和等于一个固定值。在符号语言中,我们通常使用角度的符号(如∠A、∠B、∠C)来表示三角形的各个内角,并使用等式来表示它们之间的关系。
【答案】:
$180^{\circ}$
2.三角形的内角和定理的推论.
(1)推论一:直角三角形的两个锐角
符号语言:在Rt△ABC中,∵ ∠C= 90°,
∴ ∠A+∠B= 90°.
(2)推论二:有两个角互余的三角形是
符号语言:在△ABC中,∵ ∠A+∠B= 90°,
∴ △ABC是直角三角形.
(1)推论一:直角三角形的两个锐角
互余
.符号语言:在Rt△ABC中,∵ ∠C= 90°,
∴ ∠A+∠B= 90°.
(2)推论二:有两个角互余的三角形是
直角
三角形.符号语言:在△ABC中,∵ ∠A+∠B= 90°,
∴ △ABC是直角三角形.
答案:
【解析】:
本题考查的是对三角形内角和定理的推论的理解和应用。
对于推论一,需要理解直角三角形的两个锐角是互余的,即它们的角度和为90°。
对于推论二,需要理解如果一个三角形有两个角互余,那么这个三角形一定是直角三角形。
【答案】:
(1) 推论一: 直角三角形的两个锐角互余。
符号语言: 在$Rt \bigtriangleup ABC$中,
∵ $\angle C= 90{^\circ}$,
∴ $\angle A+\angle B= 90{^\circ}$。
(2) 推论二: 有两个角互余的三角形是直角三角形。
符号语言: 在$\bigtriangleup ABC$中,
∵ $\angle A+\angle B= 90{^\circ}$,
∴ $\bigtriangleup ABC$是直角三角形。
本题考查的是对三角形内角和定理的推论的理解和应用。
对于推论一,需要理解直角三角形的两个锐角是互余的,即它们的角度和为90°。
对于推论二,需要理解如果一个三角形有两个角互余,那么这个三角形一定是直角三角形。
【答案】:
(1) 推论一: 直角三角形的两个锐角互余。
符号语言: 在$Rt \bigtriangleup ABC$中,
∵ $\angle C= 90{^\circ}$,
∴ $\angle A+\angle B= 90{^\circ}$。
(2) 推论二: 有两个角互余的三角形是直角三角形。
符号语言: 在$\bigtriangleup ABC$中,
∵ $\angle A+\angle B= 90{^\circ}$,
∴ $\bigtriangleup ABC$是直角三角形。
例1 如图,AD是△ABC的角平分线,∠B= 45°,∠ADC= 75°,求∠BAC,∠C的度数.
分析:由∠ADC的度数可知∠ADB的度数,再由∠B的度数及三角形内角和为180°可得到∠BAD的度数.由AD为角平分线得到∠BAC的度数,再由三角形内角和为180°可得到∠C的度数.

分析:由∠ADC的度数可知∠ADB的度数,再由∠B的度数及三角形内角和为180°可得到∠BAD的度数.由AD为角平分线得到∠BAC的度数,再由三角形内角和为180°可得到∠C的度数.

答案:
解:
∵∠ADC=75°,∠ADC+∠ADB=180°
∴∠ADB=180°-75°=105°
在△ABD中,∠B=45°,∠ADB=105°
∠BAD=180°-∠B-∠ADB=180°-45°-105°=30°
∵AD是△ABC的角平分线
∴∠BAC=2∠BAD=2×30°=60°
在△ABC中,∠BAC=60°,∠B=45°
∠C=180°-∠BAC-∠B=180°-60°-45°=75°
答:∠BAC=60°,∠C=75°
∵∠ADC=75°,∠ADC+∠ADB=180°
∴∠ADB=180°-75°=105°
在△ABD中,∠B=45°,∠ADB=105°
∠BAD=180°-∠B-∠ADB=180°-45°-105°=30°
∵AD是△ABC的角平分线
∴∠BAC=2∠BAD=2×30°=60°
在△ABC中,∠BAC=60°,∠B=45°
∠C=180°-∠BAC-∠B=180°-60°-45°=75°
答:∠BAC=60°,∠C=75°
1.如图,墙上钉着三根木条a,b,c,量得∠1= 70°,∠2= 100°,那么木条a,b所在直线所夹的锐角的度数是(
A.5°
B.10°
C.30°
D.70°
B
)A.5°
B.10°
C.30°
D.70°
答案:
【解析】:本题可根据平角的定义求出与$\angle1$和$\angle2$相邻的角的度数,再利用三角形内角和定理求出木条$a$,$b$所在直线所夹的锐角的度数。
步骤一:求出与$\angle1$和$\angle2$相邻的角的度数
观察图形可知,$\angle1$与它相邻的角组成一个平角,因为平角的度数为$180^{\circ}$,已知$\angle1 = 70^{\circ}$,所以与$\angle1$相邻的角的度数为$180^{\circ} - 70^{\circ} = 110^{\circ}$。
同理,$\angle2$与它相邻的角组成一个平角,已知$\angle2 = 100^{\circ}$,所以与$\angle2$相邻的角的度数为$180^{\circ} - 100^{\circ} = 80^{\circ}$。
步骤二:求出木条$a$,$b$所在直线所夹的锐角的度数
设木条$a$,$b$所在直线所夹的锐角为$\angle3$,由上述计算可知,与$\angle1$相邻的角、与$\angle2$相邻的角和$\angle3$组成一个三角形。
根据三角形内角和定理:三角形的内角和等于$180^{\circ}$,可得$\angle3 + 80^{\circ} + 110^{\circ} = 180^{\circ}$,移项可得$\angle3 = 180^{\circ} - 80^{\circ} - 110^{\circ} = 10^{\circ}$。
【答案】:B。
步骤一:求出与$\angle1$和$\angle2$相邻的角的度数
观察图形可知,$\angle1$与它相邻的角组成一个平角,因为平角的度数为$180^{\circ}$,已知$\angle1 = 70^{\circ}$,所以与$\angle1$相邻的角的度数为$180^{\circ} - 70^{\circ} = 110^{\circ}$。
同理,$\angle2$与它相邻的角组成一个平角,已知$\angle2 = 100^{\circ}$,所以与$\angle2$相邻的角的度数为$180^{\circ} - 100^{\circ} = 80^{\circ}$。
步骤二:求出木条$a$,$b$所在直线所夹的锐角的度数
设木条$a$,$b$所在直线所夹的锐角为$\angle3$,由上述计算可知,与$\angle1$相邻的角、与$\angle2$相邻的角和$\angle3$组成一个三角形。
根据三角形内角和定理:三角形的内角和等于$180^{\circ}$,可得$\angle3 + 80^{\circ} + 110^{\circ} = 180^{\circ}$,移项可得$\angle3 = 180^{\circ} - 80^{\circ} - 110^{\circ} = 10^{\circ}$。
【答案】:B。
2.(2023·遂宁)若一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
答案:
解:设三角形三个内角的度数分别为$x$,$2x$,$3x$。
因为三角形内角和为$180^{\circ}$,所以$x + 2x + 3x = 180^{\circ}$。
解得$6x = 180^{\circ}$,$x = 30^{\circ}$。
则三个内角分别为$30^{\circ}$,$2×30^{\circ}=60^{\circ}$,$3×30^{\circ}=90^{\circ}$。
所以这个三角形是直角三角形。
答案:B
因为三角形内角和为$180^{\circ}$,所以$x + 2x + 3x = 180^{\circ}$。
解得$6x = 180^{\circ}$,$x = 30^{\circ}$。
则三个内角分别为$30^{\circ}$,$2×30^{\circ}=60^{\circ}$,$3×30^{\circ}=90^{\circ}$。
所以这个三角形是直角三角形。
答案:B
3.(2022·贺州)如图,在Rt△ABC中,∠C= 90°,∠B= 56°,则∠A的度数为(
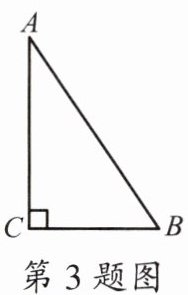
A.34°
B.44°
C.124°
D.134°
A
)
A.34°
B.44°
C.124°
D.134°
答案:
【解析】:本题可根据三角形内角和定理来求解$\angle A$的度数。
三角形内角和定理为:三角形的内角和等于$180^{\circ}$。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 56^{\circ}$,设$\angle A$的度数为$x$,根据三角形内角和定理可得$\angle A+\angle B+\angle C = 180^{\circ}$,即$x + 56^{\circ}+ 90^{\circ}= 180^{\circ}$,通过求解这个方程就能得到$\angle A$的度数。
【答案】:解:因为在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 56^{\circ}$,
根据三角形内角和为$180^{\circ}$,
所以$\angle A=180^{\circ}-\angle C - \angle B$
$=180^{\circ}- 90^{\circ}- 56^{\circ}$
$=34^{\circ}$
故选A。
三角形内角和定理为:三角形的内角和等于$180^{\circ}$。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 56^{\circ}$,设$\angle A$的度数为$x$,根据三角形内角和定理可得$\angle A+\angle B+\angle C = 180^{\circ}$,即$x + 56^{\circ}+ 90^{\circ}= 180^{\circ}$,通过求解这个方程就能得到$\angle A$的度数。
【答案】:解:因为在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 56^{\circ}$,
根据三角形内角和为$180^{\circ}$,
所以$\angle A=180^{\circ}-\angle C - \angle B$
$=180^{\circ}- 90^{\circ}- 56^{\circ}$
$=34^{\circ}$
故选A。
4.如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C= 30°,AC//EF,则∠1的度数为(
A.30°
B.45°
C.60°
D.75°
C
)A.30°
B.45°
C.60°
D.75°
答案:
解:在△ABC中,∠ABC=90°,∠C=30°,
∴∠A=180°-∠ABC-∠C=180°-90°-30°=60°。
∵AC//EF,
∴∠1=∠A=60°。
答案:C
∴∠A=180°-∠ABC-∠C=180°-90°-30°=60°。
∵AC//EF,
∴∠1=∠A=60°。
答案:C
例2 如图,在△ABC中,∠ABC,∠ACB的平分线BD,CE相交于点O.
(1)若∠ABC= 32°,∠ACB= 58°,则∠BOC的度数是
(2)若∠A= 76°,求∠BOC的度数;

(3)若∠A= α,∠BOC= β,请猜想α与β之间的数量关系,并说明理由.

注意:本题第(3)问的结论可作为常用结论记住.
(1)若∠ABC= 32°,∠ACB= 58°,则∠BOC的度数是
135°
;(2)若∠A= 76°,求∠BOC的度数;

解:∵∠A=76°,
∴∠ABC+∠ACB=180°-∠A=104°.
∵BD,CE分别平分∠ABC,∠ACB,
∴∠OBC=1/2∠ABC,∠OCB=1/2∠ACB,
∴∠OBC+∠OCB=1/2(∠ABC+∠ACB)=52°,
∴∠BOC=180°-(∠OBC+∠OCB)=128°.
∴∠ABC+∠ACB=180°-∠A=104°.
∵BD,CE分别平分∠ABC,∠ACB,
∴∠OBC=1/2∠ABC,∠OCB=1/2∠ACB,
∴∠OBC+∠OCB=1/2(∠ABC+∠ACB)=52°,
∴∠BOC=180°-(∠OBC+∠OCB)=128°.
(3)若∠A= α,∠BOC= β,请猜想α与β之间的数量关系,并说明理由.

注意:本题第(3)问的结论可作为常用结论记住.
解:β=90°+1/2α.
理由:∵∠A=α,
∴∠ABC+∠ACB=180°-α.
∵BD,CE分别平分∠ABC,∠ACB,
∴∠OBC=1/2∠ABC,∠OCB=1/2∠ACB,
∴∠OBC+∠OCB=1/2(∠ABC+∠ACB)=1/2(180°-α)=90°-1/2α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-1/2α)=90°+1/2α,
即β=90°+1/2α.
理由:∵∠A=α,
∴∠ABC+∠ACB=180°-α.
∵BD,CE分别平分∠ABC,∠ACB,
∴∠OBC=1/2∠ABC,∠OCB=1/2∠ACB,
∴∠OBC+∠OCB=1/2(∠ABC+∠ACB)=1/2(180°-α)=90°-1/2α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-1/2α)=90°+1/2α,
即β=90°+1/2α.
答案:
(1) 135°
(2) 解:
∵∠A=76°,
∴∠ABC+∠ACB=180°-∠A=104°.
∵BD,CE分别平分∠ABC,∠ACB,
∴∠OBC=1/2∠ABC,∠OCB=1/2∠ACB,
∴∠OBC+∠OCB=1/2(∠ABC+∠ACB)=52°,
∴∠BOC=180°-(∠OBC+∠OCB)=128°.
(3) 解:β=90°+1/2α.
理由:
∵∠A=α,
∴∠ABC+∠ACB=180°-α.
∵BD,CE分别平分∠ABC,∠ACB,
∴∠OBC=1/2∠ABC,∠OCB=1/2∠ACB,
∴∠OBC+∠OCB=1/2(∠ABC+∠ACB)=1/2(180°-α)=90°-1/2α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-1/2α)=90°+1/2α,
即β=90°+1/2α.
(1) 135°
(2) 解:
∵∠A=76°,
∴∠ABC+∠ACB=180°-∠A=104°.
∵BD,CE分别平分∠ABC,∠ACB,
∴∠OBC=1/2∠ABC,∠OCB=1/2∠ACB,
∴∠OBC+∠OCB=1/2(∠ABC+∠ACB)=52°,
∴∠BOC=180°-(∠OBC+∠OCB)=128°.
(3) 解:β=90°+1/2α.
理由:
∵∠A=α,
∴∠ABC+∠ACB=180°-α.
∵BD,CE分别平分∠ABC,∠ACB,
∴∠OBC=1/2∠ABC,∠OCB=1/2∠ACB,
∴∠OBC+∠OCB=1/2(∠ABC+∠ACB)=1/2(180°-α)=90°-1/2α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-1/2α)=90°+1/2α,
即β=90°+1/2α.
查看更多完整答案,请扫码查看


