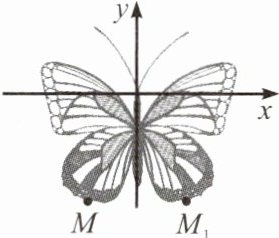
1. (2024·绵阳) 蝴蝶颜色炫丽,翩翩起舞时非常美丽,深受人们喜爱,它的图案具有对称美,如图,蝴蝶图案关于 $ y $ 轴对称,点 $ M $ 的对应点为 $ M_1 $,若点 $ M $ 的坐标为 $ (-2,-3) $,则点 $ M_1 $ 的坐标为(
A.$ (2,-3) $
B.$ (-3,2) $
C.$ (-2,3) $
D.$ (2,3) $
A
)
A.$ (2,-3) $
B.$ (-3,2) $
C.$ (-2,3) $
D.$ (2,3) $
答案:
【解析】:本题可根据关于$y$轴对称的点的坐标特征来求解点$M_1$的坐标。
关于$y$轴对称的点的坐标特征为:纵坐标不变,横坐标互为相反数。
已知点$M$的坐标为$(-2,-3)$,点$M$与点$M_1$关于$y$轴对称,那么点$M_1$的纵坐标与点$M$的纵坐标相同,即为$-3$;点$M_1$的横坐标是点$M$横坐标的相反数,$-2$的相反数是$2$,所以点$M_1$的横坐标为$2$。
因此,点$M_1$的坐标为$(2,-3)$。
【答案】:A。
关于$y$轴对称的点的坐标特征为:纵坐标不变,横坐标互为相反数。
已知点$M$的坐标为$(-2,-3)$,点$M$与点$M_1$关于$y$轴对称,那么点$M_1$的纵坐标与点$M$的纵坐标相同,即为$-3$;点$M_1$的横坐标是点$M$横坐标的相反数,$-2$的相反数是$2$,所以点$M_1$的横坐标为$2$。
因此,点$M_1$的坐标为$(2,-3)$。
【答案】:A。
2. (2022·贵港) 若点 $ A(a,-1) $ 与点 $ B(2,b) $ 关于 $ y $ 轴对称,则 $ a-b $ 的值是(
A.-1
B.-3
C.1
D.2
A
)A.-1
B.-3
C.1
D.2
答案:
【解析】:
本题主要考查平面直角坐标系中关于y轴对称的点的坐标性质。
在平面直角坐标系中,如果两点关于y轴对称,则它们的横坐标互为相反数,纵坐标相同。
根据题意,点$A(a, -1)$与点$B(2, b)$关于y轴对称,
所以我们可以得到以下两个等式:
$a = -2$ (因为点A和点B的横坐标互为相反数)
$b = -1$ (因为点A和点B的纵坐标相同)
接着我们可以求出$a-b$的值:
$a-b = (-2) - (-1) = -2 + 1 = -1$。
【答案】:
A
本题主要考查平面直角坐标系中关于y轴对称的点的坐标性质。
在平面直角坐标系中,如果两点关于y轴对称,则它们的横坐标互为相反数,纵坐标相同。
根据题意,点$A(a, -1)$与点$B(2, b)$关于y轴对称,
所以我们可以得到以下两个等式:
$a = -2$ (因为点A和点B的横坐标互为相反数)
$b = -1$ (因为点A和点B的纵坐标相同)
接着我们可以求出$a-b$的值:
$a-b = (-2) - (-1) = -2 + 1 = -1$。
【答案】:
A
例 2 如图,四边形 $ ABCD $ 各顶点的坐标分别为 $ A(-2,3) $, $ B(-3,1) $, $ C(1,-2) $, $ D(2,2) $.
(1) 画出四边形 $ ABCD $ 关于 $ y $ 轴对称的四边形 $ A'B'C'D' $;
(2) 求四边形 $ ABCD $ 的面积.
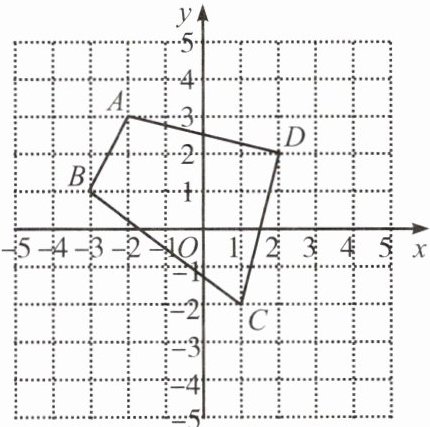
分析:(1) 分别找出 $ A $, $ B $, $ C $, $ D $ 四点关于 $ y $ 轴的对称点 $ A' $, $ B' $, $ C' $, $ D' $,然后依次连接即可;(2) 根据四边形 $ ABCD $ 的面积= 大正方形的面积-大正方形四个角上三角形的面积计算即可.
(1) 画出四边形 $ ABCD $ 关于 $ y $ 轴对称的四边形 $ A'B'C'D' $;
(2) 求四边形 $ ABCD $ 的面积.

分析:(1) 分别找出 $ A $, $ B $, $ C $, $ D $ 四点关于 $ y $ 轴的对称点 $ A' $, $ B' $, $ C' $, $ D' $,然后依次连接即可;(2) 根据四边形 $ ABCD $ 的面积= 大正方形的面积-大正方形四个角上三角形的面积计算即可.
答案:
(1) 解:关于y轴对称的点的坐标特征是横坐标互为相反数,纵坐标不变。
所以点A(-2,3)关于y轴的对称点A'(2,3);
点B(-3,1)关于y轴的对称点B'(3,1);
点C(1,-2)关于y轴的对称点C'(-1,-2);
点D(2,2)关于y轴的对称点D'(-2,2)。
在坐标系中描出A'、B'、C'、D',依次连接各点,得到四边形A'B'C'D'。
(2) 解:以点A(-2,3)、B(-3,1)、C(1,-2)、D(2,2)为顶点,构造一个边长为5的大正方形(以x=-3到x=2,y=-2到y=3为边界),其面积为5×5=25。
大正方形四个角上三角形的面积分别为:
左上角三角形(以A、(-3,3)、B为顶点):底为1,高为2,面积=1/2×1×2=1;
右上角三角形(以D、(2,3)、(3,2)为顶点):底为1,高为1,面积=1/2×1×1=0.5;
左下角三角形(以B、(-3,-2)、C为顶点):底为4,高为3,面积=1/2×4×3=6;
右下角三角形(以C、(2,-2)、D为顶点):底为1,高为4,面积=1/2×1×4=2。
四边形ABCD的面积=大正方形面积 - 四个三角形面积=25 - (1 + 0.5 + 6 + 2)=25 - 9.5=15.5。
答:四边形ABCD的面积为15.5。
(1) 解:关于y轴对称的点的坐标特征是横坐标互为相反数,纵坐标不变。
所以点A(-2,3)关于y轴的对称点A'(2,3);
点B(-3,1)关于y轴的对称点B'(3,1);
点C(1,-2)关于y轴的对称点C'(-1,-2);
点D(2,2)关于y轴的对称点D'(-2,2)。
在坐标系中描出A'、B'、C'、D',依次连接各点,得到四边形A'B'C'D'。
(2) 解:以点A(-2,3)、B(-3,1)、C(1,-2)、D(2,2)为顶点,构造一个边长为5的大正方形(以x=-3到x=2,y=-2到y=3为边界),其面积为5×5=25。
大正方形四个角上三角形的面积分别为:
左上角三角形(以A、(-3,3)、B为顶点):底为1,高为2,面积=1/2×1×2=1;
右上角三角形(以D、(2,3)、(3,2)为顶点):底为1,高为1,面积=1/2×1×1=0.5;
左下角三角形(以B、(-3,-2)、C为顶点):底为4,高为3,面积=1/2×4×3=6;
右下角三角形(以C、(2,-2)、D为顶点):底为1,高为4,面积=1/2×1×4=2。
四边形ABCD的面积=大正方形面积 - 四个三角形面积=25 - (1 + 0.5 + 6 + 2)=25 - 9.5=15.5。
答:四边形ABCD的面积为15.5。
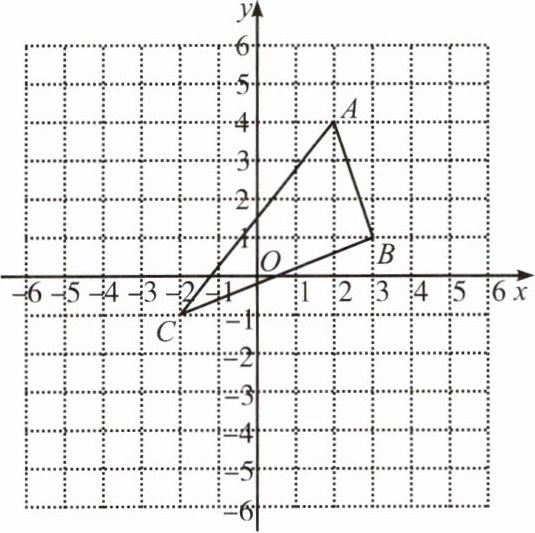
3. 如图,在平面直角坐标系中, $ A(2,4) $, $ B(3,1) $, $ C(-2,-1) $.
(1) 在图中作出 $ \triangle ABC $ 关于 $ y $ 轴的对称图形 $ \triangle A_1B_1C_1 $,并直接写出点 $ C_1 $ 的坐标;
(2) 求 $ \triangle ABC $ 的面积;
(3) 点 $ P(a,a-2) $ 与点 $ Q $ 关于 $ x $ 轴对称,若 $ PQ= 8 $,直接写出点 $ P $ 的坐标.
(1) 在图中作出 $ \triangle ABC $ 关于 $ y $ 轴的对称图形 $ \triangle A_1B_1C_1 $,并直接写出点 $ C_1 $ 的坐标;
(2) 求 $ \triangle ABC $ 的面积;
(3) 点 $ P(a,a-2) $ 与点 $ Q $ 关于 $ x $ 轴对称,若 $ PQ= 8 $,直接写出点 $ P $ 的坐标.

答案:
(1) 图略,$C_1(2,-1)$;
(2) 解:利用坐标网格,以$A(2,4)$,$B(3,1)$,$C(-2,-1)$为顶点,构建矩形,矩形长为$3 - (-2) = 5$,宽为$4 - (-1) = 5$,面积为$5×5 = 25$。减去三个直角三角形面积:$\frac{1}{2}×5×5 = 12.5$,$\frac{1}{2}×1×3 = 1.5$,$\frac{1}{2}×4×4 = 8$,$25 - 12.5 - 1.5 - 8 = 3$,即$\triangle ABC$面积为$3$;
(3) $(4,2)$或$(-4,-6)$。
(1) 图略,$C_1(2,-1)$;
(2) 解:利用坐标网格,以$A(2,4)$,$B(3,1)$,$C(-2,-1)$为顶点,构建矩形,矩形长为$3 - (-2) = 5$,宽为$4 - (-1) = 5$,面积为$5×5 = 25$。减去三个直角三角形面积:$\frac{1}{2}×5×5 = 12.5$,$\frac{1}{2}×1×3 = 1.5$,$\frac{1}{2}×4×4 = 8$,$25 - 12.5 - 1.5 - 8 = 3$,即$\triangle ABC$面积为$3$;
(3) $(4,2)$或$(-4,-6)$。
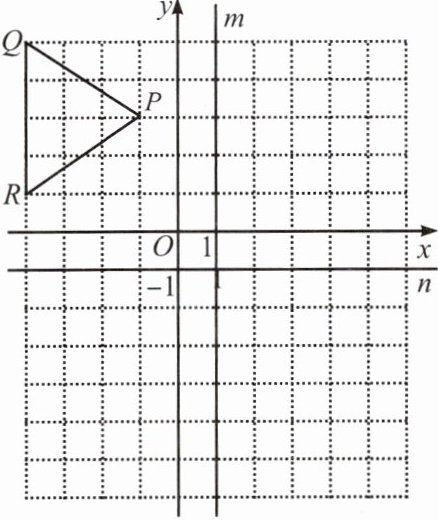
例 3 如图,在平面直角坐标系中, $ \triangle PQR $ 三点均在格点上.
(1) 分别画出 $ \triangle PQR $ 关于直线 $ m(x= 1) $ 和直线 $ n(y= -1) $ 对称的图形;
(2) 若点 $ A(x,y) $ 在 $ \triangle PQR $ 上,写出点 $ A $ 分别关于直线 $ m $ 和直线 $ n $ 对称的对应点 $ A_1 $, $ A_2 $ 的坐标.
归纳:
(1) 点 $ P(x,y) $ 关于直线 $ x= a $ 对称的点的坐标为 $ P_1(2a-x,y) $;
(2) 点 $ P(x,y) $ 关于直线 $ y= a $ 对称的点的坐标为 $ P_2(x,2a-y) $;
(3) 两点 $ M(x,m) $, $ N(x,n) $ 关于直线 $ y= \frac{m+n}{2} $ 对称;
(4) 两点 $ M(m,y) $, $ N(n,y) $ 关于直线 $ x= \frac{m+n}{2} $ 对称.
(1) 分别画出 $ \triangle PQR $ 关于直线 $ m(x= 1) $ 和直线 $ n(y= -1) $ 对称的图形;
(2) 若点 $ A(x,y) $ 在 $ \triangle PQR $ 上,写出点 $ A $ 分别关于直线 $ m $ 和直线 $ n $ 对称的对应点 $ A_1 $, $ A_2 $ 的坐标.

归纳:
(1) 点 $ P(x,y) $ 关于直线 $ x= a $ 对称的点的坐标为 $ P_1(2a-x,y) $;
(2) 点 $ P(x,y) $ 关于直线 $ y= a $ 对称的点的坐标为 $ P_2(x,2a-y) $;
(3) 两点 $ M(x,m) $, $ N(x,n) $ 关于直线 $ y= \frac{m+n}{2} $ 对称;
(4) 两点 $ M(m,y) $, $ N(n,y) $ 关于直线 $ x= \frac{m+n}{2} $ 对称.
答案:
【解析】:本题主要考查平面直角坐标系中轴对称图形的绘制以及点关于直线的对称点坐标的求解。对于(1),需要根据轴对称的性质,分别找出$\triangle PQR$各点关于直线$m(x = 1)$和直线$n(y = -1)$的对称点,然后顺次连接这些对称点得到对称图形。对于(2),利用所归纳的点关于直线对称的坐标规律来求解点$A$的对称点坐标。
(1)根据轴对称的性质,分别找出$\triangle PQR$各点关于直线$m(x = 1)$和直线$n(y = -1)$的对称点,然后顺次连接这些对称点得到对称图形(图略)。
(2)已知点$A(x,y)$,根据点关于直线对称的坐标规律:
点$P(x,y)$关于直线$x = a$对称的点的坐标为$P_1(2a - x,y)$,直线$m$的方程为$x = 1$,即$a = 1$,那么点$A(x,y)$关于直线$m$对称的对应点$A_1$的坐标为$(2×1 - x,y)$,即$A_1(2 - x,y)$。
点$P(x,y)$关于直线$y = a$对称的点的坐标为$P_2(x,2a - y)$,直线$n$的方程为$y = -1$,即$a = -1$,那么点$A(x,y)$关于直线$n$对称的对应点$A_2$的坐标为$(x,2×(-1) - y)$,即$A_2(x,-2 - y)$。
【答案】:
(1)图略;
(2)$A_1(2 - x,y)$,$A_2(x,-2 - y)$。
(1)根据轴对称的性质,分别找出$\triangle PQR$各点关于直线$m(x = 1)$和直线$n(y = -1)$的对称点,然后顺次连接这些对称点得到对称图形(图略)。
(2)已知点$A(x,y)$,根据点关于直线对称的坐标规律:
点$P(x,y)$关于直线$x = a$对称的点的坐标为$P_1(2a - x,y)$,直线$m$的方程为$x = 1$,即$a = 1$,那么点$A(x,y)$关于直线$m$对称的对应点$A_1$的坐标为$(2×1 - x,y)$,即$A_1(2 - x,y)$。
点$P(x,y)$关于直线$y = a$对称的点的坐标为$P_2(x,2a - y)$,直线$n$的方程为$y = -1$,即$a = -1$,那么点$A(x,y)$关于直线$n$对称的对应点$A_2$的坐标为$(x,2×(-1) - y)$,即$A_2(x,-2 - y)$。
【答案】:
(1)图略;
(2)$A_1(2 - x,y)$,$A_2(x,-2 - y)$。
查看更多完整答案,请扫码查看


