例2 如图,CA= CD,∠B= ∠E,∠BCE= ∠ACD.求证:AB= DE.
分析:首先证明∠ACB= ∠DCE,这是解决问题的关键,然后运用"AAS"定理证明△ABC≌△DEC,即可解决问题.
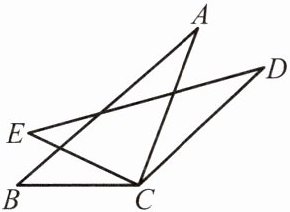
分析:首先证明∠ACB= ∠DCE,这是解决问题的关键,然后运用"AAS"定理证明△ABC≌△DEC,即可解决问题.

答案:
【解析】:根据题目所给条件,我们需要证明$∠ACB= ∠DCE$,然后通过$AAS$(角-角-边)定理证明两个三角形全等,从而得出$AB=DE$。
证明$∠ACB= ∠DCE$:
由于$∠BCE= ∠ACD$,并且$∠BCA+∠ACE=∠ACE+∠DCE$(因为$∠BCE$和$∠ACD$都是外部角,且相等),
所以可以得出$∠ACB= ∠DCE$。
运用$AAS$定理证明三角形全等:
在$△ABC$和$△DEC$中,
已知$∠B= ∠E$,$∠ACB= ∠DCE$,且$CA= CD$,
根据$AAS$定理,我们可以得出$△ABC≌△DEC$。
根据全等三角形的性质,对应边相等,所以$AB= DE$。
【答案】:证明:
∵$∠BCE= ∠ACD$,$∠BCA+∠ACE=∠ACE+∠DCE$,
∴$∠ACB= ∠DCE$,
在$△ABC$与$△DEC$中,
$\left\{\begin{matrix}∠B= ∠E,\\∠ACB= ∠DCE,\\CA= CD.\end{matrix}\right.$
∴$△ABC≌△DEC(AAS)$,
∴$AB= DE$。
证明$∠ACB= ∠DCE$:
由于$∠BCE= ∠ACD$,并且$∠BCA+∠ACE=∠ACE+∠DCE$(因为$∠BCE$和$∠ACD$都是外部角,且相等),
所以可以得出$∠ACB= ∠DCE$。
运用$AAS$定理证明三角形全等:
在$△ABC$和$△DEC$中,
已知$∠B= ∠E$,$∠ACB= ∠DCE$,且$CA= CD$,
根据$AAS$定理,我们可以得出$△ABC≌△DEC$。
根据全等三角形的性质,对应边相等,所以$AB= DE$。
【答案】:证明:
∵$∠BCE= ∠ACD$,$∠BCA+∠ACE=∠ACE+∠DCE$,
∴$∠ACB= ∠DCE$,
在$△ABC$与$△DEC$中,
$\left\{\begin{matrix}∠B= ∠E,\\∠ACB= ∠DCE,\\CA= CD.\end{matrix}\right.$
∴$△ABC≌△DEC(AAS)$,
∴$AB= DE$。
3.(2024·八中七下期中)如图,在△ABC 和△BDE 中,再添两个条件不能使△ABC 和△BDE 全等的是 (
A.AB= BD,AE= DC
B.AB= BD,DE= AC
C.BE= BC,∠E= ∠C
D.∠EAF= ∠CDF,DE= AC
B
)A.AB= BD,AE= DC
B.AB= BD,DE= AC
C.BE= BC,∠E= ∠C
D.∠EAF= ∠CDF,DE= AC
答案:
【解析】:本题考查三角形全等的判定定理。
三角形全等的判定定理有SSS(边边边)、SAS(边角边)、ASA(角边角)、AAS(角角边)和HL(斜边、直角边)。
A选项:$AB=BD$,$AE=DC$,由于$AE+AD=DC+AD$,可以得到$AC=BE$,再加上$\angle BDE=\angle BAC$,$\angle B=\angle B$,可以利用SAS定理证明$\triangle ABC\cong \triangle BDE$,故A选项不符合题意。
B选项:$AB=BD$,$DE=AC$,由于$\angle BDE=\angle BAC$,$\angle B=\angle B$,这里只给出了两边和一个非夹角,不能构成三角形全等的条件,故B选项符合题意。
C选项:$BE=BC$,$\angle E=\angle C$,再加上公共边$\angle B=\angle B$,可以利用ASA定理证明$\triangle ABC\cong \triangle BDE$,故C选项不符合题意。
D选项:$\angle EAF=\angle CDF$,由于$\angle EAF=\angle BDE$,$\angle CDF=\angle BAC$,可以得到$\angle BDE=\angle BAC$,再加上$DE=AC$,$\angle B=\angle B$,可以利用AAS定理证明$\triangle ABC\cong \triangle BDE$,故D选项不符合题意。
【答案】:B。
三角形全等的判定定理有SSS(边边边)、SAS(边角边)、ASA(角边角)、AAS(角角边)和HL(斜边、直角边)。
A选项:$AB=BD$,$AE=DC$,由于$AE+AD=DC+AD$,可以得到$AC=BE$,再加上$\angle BDE=\angle BAC$,$\angle B=\angle B$,可以利用SAS定理证明$\triangle ABC\cong \triangle BDE$,故A选项不符合题意。
B选项:$AB=BD$,$DE=AC$,由于$\angle BDE=\angle BAC$,$\angle B=\angle B$,这里只给出了两边和一个非夹角,不能构成三角形全等的条件,故B选项符合题意。
C选项:$BE=BC$,$\angle E=\angle C$,再加上公共边$\angle B=\angle B$,可以利用ASA定理证明$\triangle ABC\cong \triangle BDE$,故C选项不符合题意。
D选项:$\angle EAF=\angle CDF$,由于$\angle EAF=\angle BDE$,$\angle CDF=\angle BAC$,可以得到$\angle BDE=\angle BAC$,再加上$DE=AC$,$\angle B=\angle B$,可以利用AAS定理证明$\triangle ABC\cong \triangle BDE$,故D选项不符合题意。
【答案】:B。
4. 如图,EF,BG,DH 都垂直于 FH,AE⊥AB 且 AE= AB,BC⊥CD 且 BC= CD,请按照图中所标注的数据,计算图中阴影部分的面积 S 是
59
.
答案:
证明:
∵EF⊥FH,BG⊥FH,DH⊥FH,AE⊥AB,
∴∠EFA=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,
∴∠FEA=∠BAG,
在△EFA和△AGB中,
∠EFA=∠AGB,∠FEA=∠BAG,AE=AB,
∴△EFA≌△AGB(AAS),
∴AF=BG=3,AG=EF=6,
同理可证△BGC≌△CHD(AAS),
∴CG=DH=4,CH=BG=3,
∴FH=FA+AG+GC+CH=3+6+4+3=16,
S=梯形EFHD面积-△EFA面积-△BGC面积-△DHC面积
=1/2×(EF+DH)×FH -1/2×EF×AF -1/2×BG×CG -1/2×DH×CH
=1/2×(6+4)×16 -1/2×6×3 -1/2×3×4 -1/2×4×3
=80 -9 -6 -6=59
59
∵EF⊥FH,BG⊥FH,DH⊥FH,AE⊥AB,
∴∠EFA=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,
∴∠FEA=∠BAG,
在△EFA和△AGB中,
∠EFA=∠AGB,∠FEA=∠BAG,AE=AB,
∴△EFA≌△AGB(AAS),
∴AF=BG=3,AG=EF=6,
同理可证△BGC≌△CHD(AAS),
∴CG=DH=4,CH=BG=3,
∴FH=FA+AG+GC+CH=3+6+4+3=16,
S=梯形EFHD面积-△EFA面积-△BGC面积-△DHC面积
=1/2×(EF+DH)×FH -1/2×EF×AF -1/2×BG×CG -1/2×DH×CH
=1/2×(6+4)×16 -1/2×6×3 -1/2×3×4 -1/2×4×3
=80 -9 -6 -6=59
59
5. 如图,在△ACB 中,∠ACB= 90°,AC= BC,点 C 的坐标为(-2,0),点 A 的坐标为(-6,3),则点 B 的坐标是
(1,4)
.
答案:
解:过点A作AD⊥x轴于D,过点B作BE⊥x轴于E。
∵点C的坐标为(-2,0),点A的坐标为(-6,3),
∴OC=2,OD=6,AD=3,
∴CD=OD-OC=6-2=4。
∵∠ACB=90°,
∴∠ACD+∠BCE=90°。
∵AD⊥x轴,BE⊥x轴,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE。
在△ADC和△CEB中,
∠ADC=∠CEB,
∠CAD=∠BCE,
AC=BC,
∴△ADC≌△CEB(AAS),
∴AD=CE=3,CD=BE=4。
∵OC=2,
∴OE=CE-OC=3-2=1,
∴点B的坐标为(1,4)。
答案:(1,4)
∵点C的坐标为(-2,0),点A的坐标为(-6,3),
∴OC=2,OD=6,AD=3,
∴CD=OD-OC=6-2=4。
∵∠ACB=90°,
∴∠ACD+∠BCE=90°。
∵AD⊥x轴,BE⊥x轴,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE。
在△ADC和△CEB中,
∠ADC=∠CEB,
∠CAD=∠BCE,
AC=BC,
∴△ADC≌△CEB(AAS),
∴AD=CE=3,CD=BE=4。
∵OC=2,
∴OE=CE-OC=3-2=1,
∴点B的坐标为(1,4)。
答案:(1,4)
探究3 用"ASA""AAS"证明
例3 如图,已知∠1= ∠2,∠3= ∠4,求证:ED= EC.
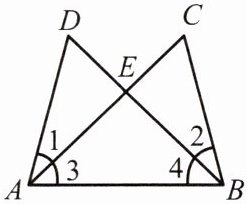
例3 如图,已知∠1= ∠2,∠3= ∠4,求证:ED= EC.

答案:
证明:
在△ABD和△ABC中,
∵∠1=∠2,AB=AB(公共边),∠3=∠4,
∴△ABD≌△ABC(ASA).
∴AD=AC.
在△ADE和△ACE中,
∵AD=AC,∠1=∠2,AE=AE(公共边),
∴△ADE≌△ACE(SAS).
∴ED=EC.
在△ABD和△ABC中,
∵∠1=∠2,AB=AB(公共边),∠3=∠4,
∴△ABD≌△ABC(ASA).
∴AD=AC.
在△ADE和△ACE中,
∵AD=AC,∠1=∠2,AE=AE(公共边),
∴△ADE≌△ACE(SAS).
∴ED=EC.
6. 如图,点 A 在 DE 上,AC= EC,∠1= ∠2= ∠3,则 DE= (
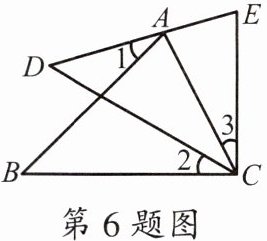
A.AB
B.BC
C.DC
D.AC
A
) 
A.AB
B.BC
C.DC
D.AC
答案:
证明:
∵∠1=∠2,∠AFD=∠CFB(对顶角相等),
∴∠D=∠B(三角形内角和定理)。
∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,即∠ACB=∠ECD。
在△ABC和△EDC中,
∠B=∠D,
∠ACB=∠ECD,
AC=EC,
∴△ABC≌△EDC(AAS)。
∴DE=AB。
答案:A
∵∠1=∠2,∠AFD=∠CFB(对顶角相等),
∴∠D=∠B(三角形内角和定理)。
∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,即∠ACB=∠ECD。
在△ABC和△EDC中,
∠B=∠D,
∠ACB=∠ECD,
AC=EC,
∴△ABC≌△EDC(AAS)。
∴DE=AB。
答案:A
7. 如图,在△ABC 中,AD⊥BC 于点 D,BE⊥AC 于点 E,AD,BE 相交于点 H,且 HD= DC= 3,AH= 1,则△ABC 的面积是
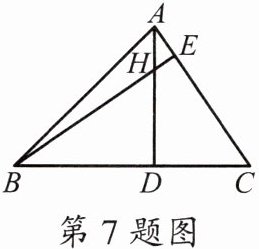
14
.
答案:
证明:
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BDH=∠AEH=90°。
∵∠AHE=∠BHD,
∴∠DAC=∠DBH。
在△ADC和△BDH中,
∠DAC=∠DBH,∠ADC=∠BDH,DC=HD,
∴△ADC≌△BDH(AAS)。
∴AD=BD。
∵AH=1,HD=3,
∴AD=AH+HD=4,
∴BD=AD=4。
∵DC=3,
∴BC=BD+DC=7。
∴S△ABC=1/2×BC×AD=1/2×7×4=14。
14
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BDH=∠AEH=90°。
∵∠AHE=∠BHD,
∴∠DAC=∠DBH。
在△ADC和△BDH中,
∠DAC=∠DBH,∠ADC=∠BDH,DC=HD,
∴△ADC≌△BDH(AAS)。
∴AD=BD。
∵AH=1,HD=3,
∴AD=AH+HD=4,
∴BD=AD=4。
∵DC=3,
∴BC=BD+DC=7。
∴S△ABC=1/2×BC×AD=1/2×7×4=14。
14
三角形全等的基本事实:三边分别相等的两个三角形
全等
(可以简写成“边边边”或“SSS”).
答案:
【解析】:本题考查三角形全等的基本事实“SSS”,即三边分别相等的两个三角形全等。题目给出了在$\bigtriangleup ABC$和$\bigtriangleup DEF$中,三边分别对应相等的情况,要求根据“SSS”判定定理得出两个三角形全等的结论。
【答案】:全等
【答案】:全等
例1 如图,在△ABC 中,$AB= AC$,D 是 BC 的中点.
求证:$△ABD\cong △ACD.$
分析:要证$△ABD\cong △ACD$,可以看这两个三角形的三条边是否相等.
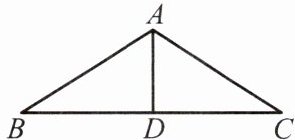
注意:两个三角形的公共边是一组对应边.
求证:$△ABD\cong △ACD.$
分析:要证$△ABD\cong △ACD$,可以看这两个三角形的三条边是否相等.

注意:两个三角形的公共边是一组对应边.
答案:
【解析】:本题考查全等三角形的判定定理——“SSS”(三边全等)。题目给出了$AB=AC$,且$D$是$BC$的中点,即$BD=CD$,同时$AD$是两个三角形的公共边,由此可以利用“SSS”定理证明两个三角形全等。
【答案】:证明:
∵$D$是$BC$的中点,
∴$BD=CD$,
在$\bigtriangleup ABD$和$\bigtriangleup ACD$中,
$\left\{\begin{matrix}AB=AC,\\BD=CD,\\AD=AD.\end{matrix}\right.$
∴$\bigtriangleup ABD\cong\bigtriangleup ACD(SSS)$。
【答案】:证明:
∵$D$是$BC$的中点,
∴$BD=CD$,
在$\bigtriangleup ABD$和$\bigtriangleup ACD$中,
$\left\{\begin{matrix}AB=AC,\\BD=CD,\\AD=AD.\end{matrix}\right.$
∴$\bigtriangleup ABD\cong\bigtriangleup ACD(SSS)$。
查看更多完整答案,请扫码查看


