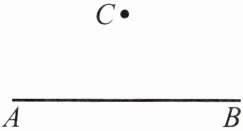
例1 如图,已知直线AB及直线AB外一点C.利用直尺和圆规过点C作直线AB的平行线CD.
分析:前面知道"同位角相
分析:前面知道"同位角相
等
,两直线平行".故可以利用这个结论,要过点C作直线AB的平行线CD.则需先作出截线,再作出相等的同位角即可.
答案:
解:作法:
1. 过点C任意作一条直线CE,交AB于点E;
2. 以点E为圆心,任意长为半径画弧,分别交EC于点F,交EB于点G;
3. 以点C为圆心,同样长为半径画弧,交CE于点H;
4. 以点H为圆心,FG长为半径画弧,交前弧于点D;
5. 过点C、D作直线CD。
则直线CD即为所求作的直线AB的平行线。
1. 过点C任意作一条直线CE,交AB于点E;
2. 以点E为圆心,任意长为半径画弧,分别交EC于点F,交EB于点G;
3. 以点C为圆心,同样长为半径画弧,交CE于点H;
4. 以点H为圆心,FG长为半径画弧,交前弧于点D;
5. 过点C、D作直线CD。
则直线CD即为所求作的直线AB的平行线。
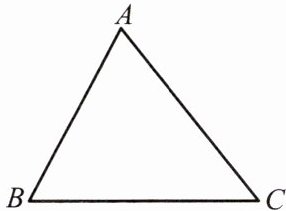
1.如图,用直尺和圆规作一条直线,使这条直线过△ABC的顶点A,并且与边BC平行.

答案:
解:
1. 以点B为圆心,任意长为半径画弧,分别交BA、BC于点D、E;
2. 以点A为圆心,BD长为半径画弧,交BA于点F;
3. 以点F为圆心,DE长为半径画弧,与步骤2中所画弧交于点G;
4. 过点A、G作直线AG。
则直线AG即为所求作的过顶点A且平行于边BC的直线。
1. 以点B为圆心,任意长为半径画弧,分别交BA、BC于点D、E;
2. 以点A为圆心,BD长为半径画弧,交BA于点F;
3. 以点F为圆心,DE长为半径画弧,与步骤2中所画弧交于点G;
4. 过点A、G作直线AG。
则直线AG即为所求作的过顶点A且平行于边BC的直线。
例2 如图,已知线段a,b和∠α,求作△ABC,使AB= a,AC= b,∠A= ∠α.
分析:先作一个角等于已知角,再在角的两边分别截取线段AB= a,AC= b,然后连接BC即得.
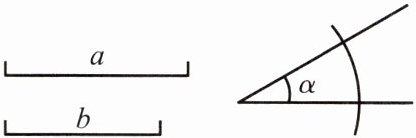
分析:先作一个角等于已知角,再在角的两边分别截取线段AB= a,AC= b,然后连接BC即得.
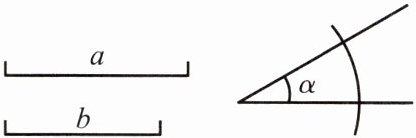
答案:
解:作法:
1. 作∠MAN=∠α;
2. 在射线AM上截取AB=a;
3. 在射线AN上截取AC=b;
4. 连接BC。
则△ABC即为所求作的三角形。
1. 作∠MAN=∠α;
2. 在射线AM上截取AB=a;
3. 在射线AN上截取AC=b;
4. 连接BC。
则△ABC即为所求作的三角形。
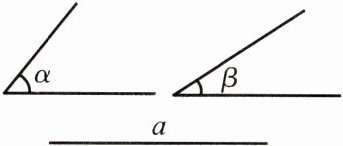
2.已知∠α,∠β和线段a,求作一个三角形,使它的两个角分别等于∠α,∠β并且两角的夹边等于a.

答案:
【解析】:
本题主要考查了利用全等三角形的判定定理来构造三角形,以及作一个角等于已知角的方法。
根据题意,需要构造一个三角形,使其两个角分别等于$\angle\alpha$和$\angle\beta$,且这两个角的夹边等于$a$。
为了构造这样的三角形,可以先作一条长度为$a$的线段,然后在这条线段的两个端点分别作出$\angle\alpha$和$\angle\beta$,从而得到满足条件的三角形。
为了确保所作三角形的准确性,可以利用全等三角形的判定定理。具体来说,可以通过证明所作三角形与某个已知三角形全等来验证其正确性。
图略,
先作一条长度为$a$的线段$AB$。
在点$A$处,利用作图工具作出$\angle\alpha$,使其一边与线段$AB$重合。
在点$B$处,同样利用作图工具作出$\angle\beta$,使其一边与线段$AB$的另一端重合。
延长$\angle\alpha$和$\angle\beta$的另一边,使它们相交于点$C$。
连接线段$AC$和$BC$,得到三角形$ABC$。
这个三角形$ABC$就是满足题目要求的三角形,即它的两个角分别等于$\angle\alpha$和$\angle\beta$,且这两个角的夹边等于$a$。
【答案】:
作法:
①作线段$AB=a$;
②在$AB$的同旁作$\angle DAB=\angle\alpha$,作$\angle EBA=\angle\beta$,$AD$,$BE$交于点$C$。
则$\bigtriangleup ABC$就是所求作的三角形。
本题主要考查了利用全等三角形的判定定理来构造三角形,以及作一个角等于已知角的方法。
根据题意,需要构造一个三角形,使其两个角分别等于$\angle\alpha$和$\angle\beta$,且这两个角的夹边等于$a$。
为了构造这样的三角形,可以先作一条长度为$a$的线段,然后在这条线段的两个端点分别作出$\angle\alpha$和$\angle\beta$,从而得到满足条件的三角形。
为了确保所作三角形的准确性,可以利用全等三角形的判定定理。具体来说,可以通过证明所作三角形与某个已知三角形全等来验证其正确性。
图略,
先作一条长度为$a$的线段$AB$。
在点$A$处,利用作图工具作出$\angle\alpha$,使其一边与线段$AB$重合。
在点$B$处,同样利用作图工具作出$\angle\beta$,使其一边与线段$AB$的另一端重合。
延长$\angle\alpha$和$\angle\beta$的另一边,使它们相交于点$C$。
连接线段$AC$和$BC$,得到三角形$ABC$。
这个三角形$ABC$就是满足题目要求的三角形,即它的两个角分别等于$\angle\alpha$和$\angle\beta$,且这两个角的夹边等于$a$。
【答案】:
作法:
①作线段$AB=a$;
②在$AB$的同旁作$\angle DAB=\angle\alpha$,作$\angle EBA=\angle\beta$,$AD$,$BE$交于点$C$。
则$\bigtriangleup ABC$就是所求作的三角形。
1.我们已经学过判定全等三角形的方法有
SSS
、SAS
、ASA
、AAS
.
答案:
SSS、SAS、ASA、AAS
2.判定直角三角形全等的方法:
符号语言:
在Rt△ABC和Rt△DEF中,
∵$\left\{\begin{array}{l} AB= DE,\\ AC= DF,\end{array} \right.$
∴Rt△ABC≌Rt△DEF(HL).
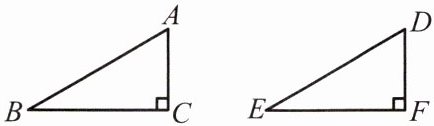
注意:前面学习的“SAS”“ASA”“AAS”“SSS”与“HL”均可以判定直角三角形全等.
斜边
和一直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).符号语言:
在Rt△ABC和Rt△DEF中,
∵$\left\{\begin{array}{l} AB= DE,\\ AC= DF,\end{array} \right.$
∴Rt△ABC≌Rt△DEF(HL).
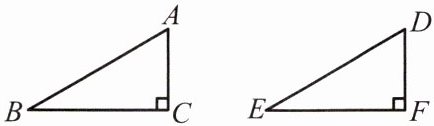
注意:前面学习的“SAS”“ASA”“AAS”“SSS”与“HL”均可以判定直角三角形全等.
答案:
【解析】:本题考查直角三角形全等的判定方法,特别是“斜边、直角边”(HL)定理。根据题目描述,需要填写与一直角边分别相等的两个直角三角形全等的另一条件,即斜边。
【答案】:斜边
【答案】:斜边
查看更多完整答案,请扫码查看


