《2025年巅峰对决八年级数学上册人教版》

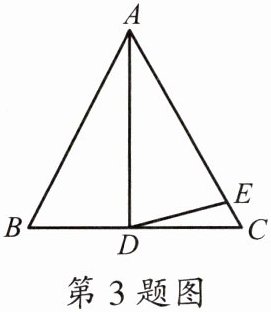
3.如图,在△ABC 中,AB= AC= BC,∠BAD= 30°,AE= AD,则∠CDE 的度数是(C)


A.10°
B.12.5°
C.15°
D.20°

答案： 解：
∵AB=AC=BC，
∴△ABC是等边三角形，
∴∠BAC=∠B=∠C=60°．
∵∠BAD=30°，
∴∠DAE=∠BAC - ∠BAD=60° - 30°=30°．
∵AE=AD，
∴△ADE是等腰三角形，
∴∠ADE=∠AED=(180° - ∠DAE)/2=(180° - 30°)/2=75°．
∵∠ADC是△ABD的外角，
∴∠ADC=∠B + ∠BAD=60° + 30°=90°．
∵∠ADC=∠ADE + ∠CDE，
∴∠CDE=∠ADC - ∠ADE=90° - 75°=15°．
答案：C

4.如图,在△ABC 中,AB= AC,∠A= 120°,BC= 6 cm,AB 的垂直平分线交 BC 于点 M,交 AB 于点 E,AC 的垂直平分线交 BC 于点 N,交 AC 于点 F,则 MN的长为(C)
A.4 cm
B.3 cm
C.2 cm
D.1 cm

答案： 【解析】：本题可先连接$AM$、$AN$，根据线段垂直平分线的性质得到$MA = MB$，$NA = NC$，再结合等腰三角形的性质以及三角形内角和定理求出$\angle B$、$\angle C$、$\angle BAM$、$\angle CAN$的度数，进而推出$\triangle AMN$是等边三角形，最后求出$MN$的长度。
步骤一：求$\angle B$和$\angle C$的度数
已知在$\triangle ABC$中，$AB = AC$，$\angle A = 120^{\circ}$，根据等腰三角形两底角相等以及三角形内角和为$180^{\circ}$，可得：
$\angle B=\angle C=\frac{1}{2}×(180^{\circ}-\angle A)=\frac{1}{2}×(180 - 120)^{\circ}= 30^{\circ}$
步骤二：根据线段垂直平分线的性质得到相关线段相等
因为$ME$是$AB$的垂直平分线，$NF$是$AC$的垂直平分线，根据线段垂直平分线上的点到这条线段的两个端点的距离相等，可得：
$MA = MB$，$NA = NC$
步骤三：求$\angle BAM$和$\angle CAN$的度数
由于$MA = MB$，所以$\angle B = \angle BAM = 30^{\circ}$；同理，因为$NA = NC$，所以$\angle C = \angle CAN = 30^{\circ}$。
步骤四：求$\angle MAN$的度数
根据三角形内角和定理，可得：
$\angle MAN=\angle A - \angle BAM - \angle CAN=120^{\circ}- 30^{\circ}- 30^{\circ}= 60^{\circ}$
步骤五：求$\angle AMN$和$\angle ANM$的度数
在$\triangle ABM$中，$\angle AMN$是$\triangle ABM$的外角，根据三角形外角等于与它不相邻的两个内角之和，可得：
$\angle AMN=\angle B + \angle BAM = 30^{\circ}+ 30^{\circ}= 60^{\circ}$
同理，在$\triangle ACN$中，$\angle ANM=\angle C + \angle CAN = 30^{\circ}+ 30^{\circ}= 60^{\circ}$
步骤六：证明$\triangle AMN$是等边三角形
因为$\angle AMN = \angle ANM = \angle MAN = 60^{\circ}$，根据三个角都相等的三角形是等边三角形，所以$\triangle AMN$是等边三角形。
步骤七：求$MN$的长度
因为$\angle B = \angle BAM = 30^{\circ}$，所以$BM = AM$，又因为$\triangle AMN$是等边三角形，所以$AM = MN = AN$，那么$BM = MN = CN$。
已知$BC = 6cm$，即$BM + MN + CN = 6cm$，所以$MN = \frac{1}{3}× BC = \frac{1}{3}× 6 = 2cm$。
【答案】：C

例3 如图,C 是线段 AB 上的一点,△ACD 和△BCE 都是等边三角形.
(1)求证:AE= DB;
(2)若 AE 交 CD 于点 M,BD 交 CE 于点 N,连接 MN,试判断△MCN 的形状,并说明理由.

答案： 【解析】：
(1) 本题可通过证明三角形全等得出对应边相等，进而证明$AE = DB$。
已知$\triangle ACD$和$\triangle BCE$都是等边三角形，根据等边三角形的性质可知$AC = CD$，$CE = CB$，$\angle ACD = \angle BCE = 60^{\circ}$，由此可推出$\angle ACE = \angle DCB$，再利用全等三角形的判定定理（$SAS$）证明$\triangle ACE\cong\triangle DCB$，最后根据全等三角形的性质得到$AE = DB$。
(2) 要判断$\triangle MCN$的形状，可先根据全等三角形的性质得到对应角相等，再结合已知条件推出$\angle MCN = 60^{\circ}$，同时证明$\triangle ACM\cong\triangle DCN$得到$CM = CN$，进而根据等边三角形的判定定理得出$\triangle MCN$的形状。
【答案】：
(1) 证明：
∵$\triangle ACD$和$\triangle BCE$都是等边三角形，
∴$AC = CD$，$CE = CB$，$\angle ACD = \angle BCE = 60^{\circ}$。
∴$\angle ACD + \angle DCE = \angle BCE + \angle DCE$，即$\angle ACE = \angle DCB$。
在$\triangle ACE$和$\triangle DCB$中，
$\begin{cases}AC = CD\\\angle ACE = \angle DCB\\CE = CB\end{cases}$
∴$\triangle ACE\cong\triangle DCB(SAS)$。
∴$AE = DB$。
(2) $\triangle MCN$是等边三角形。理由如下：
由
(1)知$\triangle ACE\cong\triangle DCB$，
∴$\angle CAE = \angle CDB$。
∵$\angle ACD = \angle BCE = 60^{\circ}$，
∴$\angle DCE = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ}$，即$\angle MCN = 60^{\circ}$。
在$\triangle ACM$和$\triangle DCN$中，
$\begin{cases}\angle CAM = \angle CDN\\AC = DC\\\angle ACM = \angle DCN = 60^{\circ}\end{cases}$
∴$\triangle ACM\cong\triangle DCN(ASA)$。
∴$CM = CN$。
又
∵$\angle MCN = 60^{\circ}$，
∴$\triangle MCN$是等边三角形。

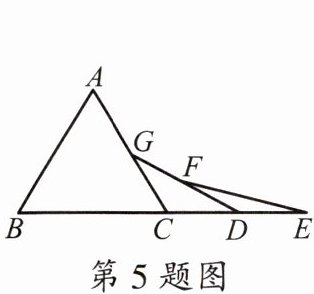
5.如图,已知△ABC 是等边三角形,点 B,C,D,E 在同一直线上,且 CG= CD,DF= DE,则∠E= ______15°.

答案： 【解析】：本题可根据等边三角形的性质求出$\angle ACB$的度数，再结合等腰三角形的性质以及三角形外角的性质求出$\angle E$的度数。
步骤一：根据等边三角形的性质求出$\angle ACB$的度数
已知$\triangle ABC$是等边三角形，根据等边三角形的性质：等边三角形的三个内角都相等，且都等于$60^{\circ}$，可得$\angle ACB = 60^{\circ}$。
步骤二：根据等腰三角形的性质求出$\angle CGD$的度数
因为$CG = CD$，所以$\triangle CGD$是等腰三角形，根据等腰三角形的性质：等腰三角形的两个底角相等，以及三角形内角和为$180^{\circ}$，可得$\angle CGD=\angle CDG$。
又因为$\angle ACB$是$\triangle CGD$的一个外角，根据三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角之和，所以$\angle ACB=\angle CGD + \angle CDG$，即$60^{\circ}=2\angle CDG$，则$\angle CDG = 30^{\circ}$。
步骤三：根据等腰三角形的性质求出$\angle E$的度数
因为$DF = DE$，所以$\triangle DEF$是等腰三角形，$\angle E=\angle DFE$。
而$\angle CDG$是$\triangle DEF$的一个外角，根据三角形外角的性质可得$\angle CDG=\angle E + \angle DFE$，即$30^{\circ}=2\angle E$，所以$\angle E = 15^{\circ}$。
【答案】：$15^{\circ}$

6.如图,AD 是△ABC 的中线,∠ADC= 60°,BC= 6,把△ABC 沿直线 AD 折叠,点 C 落在点 C'处,连接 BC',则 BC'的长为3.

答案： 解：
∵AD是△ABC的中线，BC=6，
∴BD=DC=3。
由折叠性质得：DC'=DC=3，∠ADC'=∠ADC=60°。
∵∠ADC+∠ADB=180°，
∴∠ADB=180°-60°=120°。
∵∠ADC'+∠BDC'=∠ADB，
∴∠BDC'=∠ADB-∠ADC'=120°-60°=60°。
在△BDC'中，BD=DC'=3，∠BDC'=60°，
∴△BDC'是等边三角形，
∴BC'=BD=3。
3

1. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
符号语言:如图,在Rt△ABC中,
∵∠C= 90°,∠A= 30°,

∴BC=$\frac{1}{2}AB$.
思考:你能证明这个结论吗?
证明：延长BC至点D，使CD=BC，连接AD。
∵∠C=90°，
∴∠ACD=90°。
在△ABC和△ADC中，
$BC=DC$，∠ACB=∠ACD，AC=AC，
∴△ABC≌△ADC（SAS）。
∴AB=AD，∠BAC=∠DAC=30°。
∴∠BAD=60°。
∴△ABD是等边三角形。
∴AB=BD。
∵BD=BC+CD=2BC，
∴AB=2BC，即BC=$\frac{1}{2}AB$。

答案： 斜边的一半；$\frac{1}{2}AB$
证明：延长BC至点D，使CD=BC，连接AD。
∵∠C=90°，
∴∠ACD=90°。
在△ABC和△ADC中，
$BC=DC$，∠ACB=∠ACD，AC=AC，
∴△ABC≌△ADC（SAS）。
∴AB=AD，∠BAC=∠DAC=30°。
∴∠BAD=60°。
∴△ABD是等边三角形。
∴AB=BD。
∵BD=BC+CD=2BC，
∴AB=2BC，即BC=$\frac{1}{2}AB$。