《2025年巅峰对决八年级数学上册人教版》

3.如图,∠BDC= 90°,∠B= 20°,∠C= 40°,则∠A的度数是30°.

答案： 【解析】：本题考查三角形外角的性质，即三角形的一个外角等于与它不相邻的两个内角之和。在本题中，可延长$CD$交$AB$于点$E$，利用外角性质来求解$\angle A$的度数。
延长$CD$交$AB$于点$E$。
因为$\angle BDC = 90^{\circ}$，$\angle B = 20^{\circ}$，在$\triangle BDE$中，根据三角形内角和为$180^{\circ}$，可得$\angle BED = 180^{\circ} - \angle B - \angle BDE = 180^{\circ} - 20^{\circ} - 90^{\circ} = 70^{\circ}$。
又因为$\angle BED$是$\triangle AEC$的一个外角，$\angle C = 40^{\circ}$，根据三角形外角的性质，$\angle BED=\angle A + \angle C$，所以$\angle A = \angle BED - \angle C = 70^{\circ} - 40^{\circ} = 30^{\circ}$。
【答案】：$30^{\circ}$

4.如图,在△ABC中,D,E分别是边AB和BC上的点.若∠B= 35°,∠C= 56°,∠F= 47°,则∠ADF的度数为______.

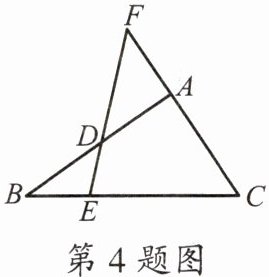
42°

答案： 解：在△ABC中，∠BAC=180°-∠B-∠C=180°-35°-56°=89°。
∵∠BAC是△ADF的外角，
∴∠BAC=∠F+∠ADF。
∴∠ADF=∠BAC-∠F=89°-47°=42°。
42°

(1)探究2:如图2,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.
∠BOC = 1/2∠A，理由如下：
∵BO和CO分别是∠ABC和∠ACD的平分线，
∴∠OBC = 1/2∠ABC，∠OCD = 1/2∠ACD，
∵∠ACD是△ABC的外角，
∴∠ACD = ∠A + ∠ABC，
∴∠OCD = 1/2(∠A + ∠ABC) = 1/2∠A + 1/2∠ABC，
∵∠OCD是△BOC的外角，
∴∠OCD = ∠BOC + ∠OBC，
∴∠BOC = ∠OCD - ∠OBC = 1/2∠A + 1/2∠ABC - 1/2∠ABC = 1/2∠A。
(2)探究3:如图3,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论:∠BOC = 90° - 1/2∠A.

答案：
(1)∠BOC = 1/2∠A，理由如下：
∵BO和CO分别是∠ABC和∠ACD的平分线，
∴∠OBC = 1/2∠ABC，∠OCD = 1/2∠ACD，
∵∠ACD是△ABC的外角，
∴∠ACD = ∠A + ∠ABC，
∴∠OCD = 1/2(∠A + ∠ABC) = 1/2∠A + 1/2∠ABC，
∵∠OCD是△BOC的外角，
∴∠OCD = ∠BOC + ∠OBC，
∴∠BOC = ∠OCD - ∠OBC = 1/2∠A + 1/2∠ABC - 1/2∠ABC = 1/2∠A。
(2)∠BOC = 90° - 1/2∠A

5.如图,在△ABC中,∠A= 64°,∠ABC和∠ACD的平分线交于点$A_1,$得$∠A_1;∠A_1BC$和$∠A_1CD$的平分线交于点$A_2,$得$∠A_2……$依次类推,则$∠A_4= $$4^{\circ}$.

答案： 【解析】：本题可根据三角形外角的性质以及角平分线的定义，找出$\angle A_n$与$\angle A$之间的规律，进而求出$\angle A_4$的值。
步骤一：根据三角形外角的性质和角平分线的定义，求出$\angle A_1$与$\angle A$的关系
在$\triangle ABC$中，根据三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角之和，可得$\angle ACD = \angle A + \angle ABC$。
因为$BA_1$平分$\angle ABC$，$CA_1$平分$\angle ACD$，所以$\angle A_1BC=\frac{1}{2}\angle ABC$，$\angle A_1CD=\frac{1}{2}\angle ACD$。
又因为$\angle A_1CD = \angle A_1 + \angle A_1BC$，即$\frac{1}{2}\angle ACD = \angle A_1 + \frac{1}{2}\angle ABC$，将$\angle ACD = \angle A + \angle ABC$代入可得：
$\frac{1}{2}(\angle A + \angle ABC) = \angle A_1 + \frac{1}{2}\angle ABC$
$\frac{1}{2}\angle A + \frac{1}{2}\angle ABC = \angle A_1 + \frac{1}{2}\angle ABC$
两边同时减去$\frac{1}{2}\angle ABC$，可得$\angle A_1 = \frac{1}{2}\angle A$。
步骤二：同理求出$\angle A_2$与$\angle A_1$的关系，进而得到$\angle A_2$与$\angle A$的关系
在$\triangle A_1BC$中，$\angle A_1CD$是$\triangle A_1BC$的外角，则$\angle A_1CD = \angle A_1 + \angle A_1BC$。
因为$BA_2$平分$\angle A_1BC$，$CA_2$平分$\angle A_1CD$，所以$\angle A_2BC=\frac{1}{2}\angle A_1BC$，$\angle A_2CD=\frac{1}{2}\angle A_1CD$。
又因为$\angle A_2CD = \angle A_2 + \angle A_2BC$，即$\frac{1}{2}\angle A_1CD = \angle A_2 + \frac{1}{2}\angle A_1BC$，将$\angle A_1CD = \angle A_1 + \angle A_1BC$代入可得：
$\frac{1}{2}(\angle A_1 + \angle A_1BC) = \angle A_2 + \frac{1}{2}\angle A_1BC$
$\frac{1}{2}\angle A_1 + \frac{1}{2}\angle A_1BC = \angle A_2 + \frac{1}{2}\angle A_1BC$
两边同时减去$\frac{1}{2}\angle A_1BC$，可得$\angle A_2 = \frac{1}{2}\angle A_1$。
将$\angle A_1 = \frac{1}{2}\angle A$代入$\angle A_2 = \frac{1}{2}\angle A_1$，可得$\angle A_2 = \frac{1}{2}×\frac{1}{2}\angle A = (\frac{1}{2})^2\angle A$。
步骤三：通过归纳推理，得到$\angle A_n$与$\angle A$的关系
由前面的推理可知$\angle A_1 = \frac{1}{2}\angle A$，$\angle A_2 = (\frac{1}{2})^2\angle A$，以此类推，可得$\angle A_n = (\frac{1}{2})^n\angle A$。
步骤四：将$n = 4$，$\angle A = 64^{\circ}$代入$\angle A_n = (\frac{1}{2})^n\angle A$，求出$\angle A_4$的值
当$n = 4$时，$\angle A_4 = (\frac{1}{2})^4×64^{\circ}=\frac{1}{16}×64^{\circ}= 4^{\circ}$。
【答案】：$4^{\circ}$

6.如图,BP是∠ABC的平分线,CP是∠ACM的平分线,∠ABP= 20°,∠ACP= 50°,则∠ADP= ______.

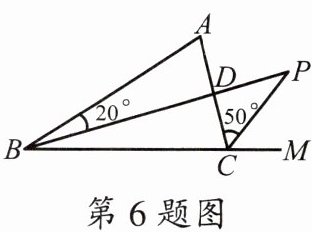
80°

答案： 解：
∵BP平分∠ABC，∠ABP=20°，
∴∠ABC=2∠ABP=40°，∠PBC=∠ABP=20°．
∵CP平分∠ACM，∠ACP=50°，
∴∠ACM=2∠ACP=100°，∠PCM=∠ACP=50°．
∵∠ACM是△ABC的外角，
∴∠BAC=∠ACM-∠ABC=100°-40°=60°．
∵∠PCM是△PBC的外角，
∴∠P=∠PCM-∠PBC=50°-20°=30°．
在△ABD中，∠BAC=60°，∠ABP=20°，
∴∠ADB=180°-∠BAC-∠ABP=180°-60°-20°=100°．
∵∠ADB+∠ADP=180°，
∴∠ADP=180°-∠ADB=180°-100°=80°．
80°

7.如图,在△ABC中,∠B= 40°,∠C= 60°,AE,AD分别是角平分线和高,则∠DAE的度数是______.

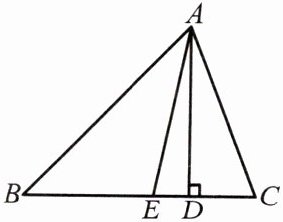
10°

答案： 解：在△ABC中，∠B=40°，∠C=60°，
∠BAC=180°-∠B-∠C=80°.
∵AE是角平分线，
∴∠BAE=∠BAC/2=40°.
∵AD是高，
∴∠ADB=90°，
∠BAD=90°-∠B=50°.
∠DAE=∠BAD-∠BAE=50°-40°=10°.
10°