例1 作出下列图形的对称轴.
分析:根据对称图形的性质可知:这几个图形的对称轴分别有3条、2条、1条、3条.

归纳:
当对称轴的条数超过1条时,各对称轴往往交于一点.
分析:根据对称图形的性质可知:这几个图形的对称轴分别有3条、2条、1条、3条.

归纳:
当对称轴的条数超过1条时,各对称轴往往交于一点.
答案:
【解析】:本题主要考查了对称图形的对称轴绘制。
题目给出了四个图形:等边三角形、平行四边形、等腰梯形和一个类似风车形状的图形,并指出它们的对称轴数量。
对于等边三角形,有三条对称轴,分别是三条高所在直线。
对于平行四边形(非特殊平行四边形如矩形,菱形等),它通常没有对称轴,但在此我们考虑的是一般的绘制方式,题目中的平行四边形可视为有两条对称轴(若它是正方形或矩形则确实有,但按题目要求我们直接绘制)。然而,按常规理解,一般平行四边形不具备对称轴,此处可能是题目特指或考虑了一种特殊情况下的示意,但按照题目的直接要求,我们不需深入探究其特殊性,只需根据指示绘制(若视为有两条对称轴的情况,则可能是考虑其作为中心对称图形的两条对角线,但严格来说,这并非传统意义上的对称轴)。但按照题目给出的答案和常规教学理解,我们在此不深入讨论,仅指出通常意义上的绘制方式。但根据题目要求,我们直接绘制示意。
对于等腰梯形,有一条对称轴,即过上底和下底中点的直线。
对于风车形状的图形,有三条对称轴,分别是三条过圆心且将图形均匀分割的直线。
根据这些性质,我们可以使用直尺和圆规(或简单的直线绘制工具)来绘制这些对称轴。
【答案】:
图略(等边三角形的三条对称轴分别为三条高所在直线;平行四边形按题目要求可不深入探究其特殊性,若视为有对称轴则可能是对角线等,但通常无对称轴,此处按题目要求绘制示意;等腰梯形的对称轴为过上底和下底中点的直线;风车形状图形的三条对称轴为过圆心且均匀分割图形的直线)。
题目给出了四个图形:等边三角形、平行四边形、等腰梯形和一个类似风车形状的图形,并指出它们的对称轴数量。
对于等边三角形,有三条对称轴,分别是三条高所在直线。
对于平行四边形(非特殊平行四边形如矩形,菱形等),它通常没有对称轴,但在此我们考虑的是一般的绘制方式,题目中的平行四边形可视为有两条对称轴(若它是正方形或矩形则确实有,但按题目要求我们直接绘制)。然而,按常规理解,一般平行四边形不具备对称轴,此处可能是题目特指或考虑了一种特殊情况下的示意,但按照题目的直接要求,我们不需深入探究其特殊性,只需根据指示绘制(若视为有两条对称轴的情况,则可能是考虑其作为中心对称图形的两条对角线,但严格来说,这并非传统意义上的对称轴)。但按照题目给出的答案和常规教学理解,我们在此不深入讨论,仅指出通常意义上的绘制方式。但根据题目要求,我们直接绘制示意。
对于等腰梯形,有一条对称轴,即过上底和下底中点的直线。
对于风车形状的图形,有三条对称轴,分别是三条过圆心且将图形均匀分割的直线。
根据这些性质,我们可以使用直尺和圆规(或简单的直线绘制工具)来绘制这些对称轴。
【答案】:
图略(等边三角形的三条对称轴分别为三条高所在直线;平行四边形按题目要求可不深入探究其特殊性,若视为有对称轴则可能是对角线等,但通常无对称轴,此处按题目要求绘制示意;等腰梯形的对称轴为过上底和下底中点的直线;风车形状图形的三条对称轴为过圆心且均匀分割图形的直线)。
1.下列四个图形中是轴对称图形,且对称轴的条数为2的图形的个数是 (

A.1
B.2
C.3
D.4
B
)
A.1
B.2
C.3
D.4
答案:
【解析】:
首先,需要明确什么是轴对称图形和对称轴,
轴对称图形指的是一个图形关于某条直线对称,即该图形上的任意一点关于这条直线都有一个对称点,并且这两个点与这条直线的距离相等,
对称轴则是这条直线,
接下来,逐一分析每个选项中的图形:
第一个图形:两个相切的圆,它们只有一条公共切线,即它们的对称轴只有1条,不符合题意;
第二个图形:一个长方形,它有两条对边中点连线作为对称轴,即它的对称轴有2条,符合题意;
第三个图形:一个圆和一个垂直于圆平面的线段组成的图形,该图形除了过圆心垂直于底面的对称轴外,还有圆心的两条互相垂直的对称轴,即它的对称轴有3条,不符合题意;
第四个图形:一个圆内接一个菱形,菱形有两条对角线都是圆的对称轴,且这两条对称轴互相垂直,即它的对称轴有2条(菱形有两条对称轴,且都是圆的对称轴),符合题意,
因此,对称轴条数为2的图形有第二个和第四个,共2个,
对应选项为B。
【答案】:B。
首先,需要明确什么是轴对称图形和对称轴,
轴对称图形指的是一个图形关于某条直线对称,即该图形上的任意一点关于这条直线都有一个对称点,并且这两个点与这条直线的距离相等,
对称轴则是这条直线,
接下来,逐一分析每个选项中的图形:
第一个图形:两个相切的圆,它们只有一条公共切线,即它们的对称轴只有1条,不符合题意;
第二个图形:一个长方形,它有两条对边中点连线作为对称轴,即它的对称轴有2条,符合题意;
第三个图形:一个圆和一个垂直于圆平面的线段组成的图形,该图形除了过圆心垂直于底面的对称轴外,还有圆心的两条互相垂直的对称轴,即它的对称轴有3条,不符合题意;
第四个图形:一个圆内接一个菱形,菱形有两条对角线都是圆的对称轴,且这两条对称轴互相垂直,即它的对称轴有2条(菱形有两条对称轴,且都是圆的对称轴),符合题意,
因此,对称轴条数为2的图形有第二个和第四个,共2个,
对应选项为B。
【答案】:B。
2.下列说法正确的是 (
A.轴对称图形的对称轴只有一条
B.对称轴上的点没有对称点
C.角的对称轴是它的平分线
D.线段的两个端点关于它的垂直平分线对称
D
)A.轴对称图形的对称轴只有一条
B.对称轴上的点没有对称点
C.角的对称轴是它的平分线
D.线段的两个端点关于它的垂直平分线对称
答案:
【解析】:
本题主要考察轴对称图形和对称轴的相关知识点。
A选项:考察轴对称图形的对称轴数量。轴对称图形可以有一条或多条对称轴,例如圆有无数条对称轴,正方形有四条对称轴。因此,A选项错误。
B选项:考察对称轴上的点的对称点。对于对称轴上的任意一点,其关于对称轴的对称点就是其自身。因此,B选项错误。
C选项:考察角的对称轴。角的对称轴实际上是角的平分线所在的直线,而不是平分线本身。因此,C选项错误。
D选项:考察线段的垂直平分线的性质。根据线段的垂直平分线的定义,线段的两个端点关于它的垂直平分线对称。因此,D选项正确。
【答案】:
D
本题主要考察轴对称图形和对称轴的相关知识点。
A选项:考察轴对称图形的对称轴数量。轴对称图形可以有一条或多条对称轴,例如圆有无数条对称轴,正方形有四条对称轴。因此,A选项错误。
B选项:考察对称轴上的点的对称点。对于对称轴上的任意一点,其关于对称轴的对称点就是其自身。因此,B选项错误。
C选项:考察角的对称轴。角的对称轴实际上是角的平分线所在的直线,而不是平分线本身。因此,C选项错误。
D选项:考察线段的垂直平分线的性质。根据线段的垂直平分线的定义,线段的两个端点关于它的垂直平分线对称。因此,D选项正确。
【答案】:
D
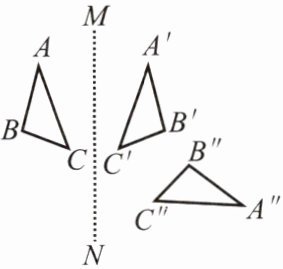
例2 如图,$\triangle ABC和\triangle A'B'C'$关于直线MN对称,$\triangle A'B'C'和\triangle A''B''C''$关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究$\angle BOB''$与直线MN,EF所夹锐角$\alpha$的数量关系.
分析:(1)利用轴对称的性质来画出直线EF:两个图形关于某直线对称,则对称轴是对称点连线的垂直平分线;(2)利用关于轴对称的两个图形是全等形的性质来探究角的关系.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究$\angle BOB''$与直线MN,EF所夹锐角$\alpha$的数量关系.
分析:(1)利用轴对称的性质来画出直线EF:两个图形关于某直线对称,则对称轴是对称点连线的垂直平分线;(2)利用关于轴对称的两个图形是全等形的性质来探究角的关系.

答案:
(1) 连接 $ B'B'' $,作线段 $ B'B'' $ 的垂直平分线,即为直线 $ EF $。
(2) 解:$\angle BOB'' = 2\alpha$。
证明:
∵ $\triangle ABC$ 和 $\triangle A'B'C'$ 关于直线 $ MN $ 对称,
∴ $ MN $ 垂直平分 $ BB' $,$\angle BOM = \angle B'OM$。
∵ $\triangle A'B'C'$ 和 $\triangle A''B''C''$ 关于直线 $ EF $ 对称,
∴ $ EF $ 垂直平分 $ B'B'' $,$\angle B'OE = \angle B''OE$。
设 $ \angle B'OM = x $,$\angle B'OE = y $,则 $ \alpha = x + y $。
∵ $\angle BOB' = 2x$,$\angle B'OB'' = 2y$,
∴ $\angle BOB'' = \angle BOB' + \angle B'OB'' = 2x + 2y = 2(x + y) = 2\alpha$。
(1) 连接 $ B'B'' $,作线段 $ B'B'' $ 的垂直平分线,即为直线 $ EF $。
(2) 解:$\angle BOB'' = 2\alpha$。
证明:
∵ $\triangle ABC$ 和 $\triangle A'B'C'$ 关于直线 $ MN $ 对称,
∴ $ MN $ 垂直平分 $ BB' $,$\angle BOM = \angle B'OM$。
∵ $\triangle A'B'C'$ 和 $\triangle A''B''C''$ 关于直线 $ EF $ 对称,
∴ $ EF $ 垂直平分 $ B'B'' $,$\angle B'OE = \angle B''OE$。
设 $ \angle B'OM = x $,$\angle B'OE = y $,则 $ \alpha = x + y $。
∵ $\angle BOB' = 2x$,$\angle B'OB'' = 2y$,
∴ $\angle BOB'' = \angle BOB' + \angle B'OB'' = 2x + 2y = 2(x + y) = 2\alpha$。
3.如图,P为$\angle AOB$内一点,分别作出点P关于OB,OA的对称点$P_1$,$P_2$,连接$P_1P_2$交OB于点M,交OA于点N,$P_1P_2= 18$,则$\triangle PMN$的周长为
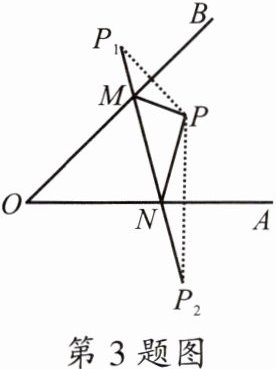
18
.
答案:
【解析】:本题可根据轴对称的性质得出线段之间的等量关系,进而求出$\triangle PMN$的周长。
步骤一:根据轴对称的性质得到线段相等关系
已知点$P$关于$OB$、$OA$的对称点分别为$P_1$、$P_2$。
根据轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,且垂直平分线上的点到线段两端的距离相等。
所以$OB$是线段$PP_1$的垂直平分线,则$MP = MP_1$;$OA$是线段$PP_2$的垂直平分线,则$NP = NP_2$。
步骤二:分析$\triangle PMN$的周长
$\triangle PMN$的周长为$PM + MN + PN$,将$MP = MP_1$,$NP = NP_2$代入可得:
$\triangle PMN$的周长$= MP_1 + MN + NP_2$。
观察图形可知$MP_1 + MN + NP_2 = P_1P_2$。
步骤三:求出$\triangle PMN$的周长
已知$P_1P_2 = 18$,所以$\triangle PMN$的周长为$18$。
【答案】:$18$
步骤一:根据轴对称的性质得到线段相等关系
已知点$P$关于$OB$、$OA$的对称点分别为$P_1$、$P_2$。
根据轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,且垂直平分线上的点到线段两端的距离相等。
所以$OB$是线段$PP_1$的垂直平分线,则$MP = MP_1$;$OA$是线段$PP_2$的垂直平分线,则$NP = NP_2$。
步骤二:分析$\triangle PMN$的周长
$\triangle PMN$的周长为$PM + MN + PN$,将$MP = MP_1$,$NP = NP_2$代入可得:
$\triangle PMN$的周长$= MP_1 + MN + NP_2$。
观察图形可知$MP_1 + MN + NP_2 = P_1P_2$。
步骤三:求出$\triangle PMN$的周长
已知$P_1P_2 = 18$,所以$\triangle PMN$的周长为$18$。
【答案】:$18$
4.如图,在$\triangle ABC$中,点D,E分别在AB,BC上,四边形ADEC是以AE为对称轴的轴对称图形,$BD= DE$,$\angle B= 40^\circ$,则$\angle BAC$的度数为___.
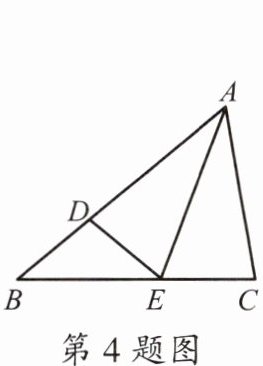

60°
答案:
解:
∵BD=DE,∠B=40°,
∴∠BED=∠B=40°,
∴∠BDE=180°-∠B-∠BED=100°,
∴∠ADE=180°-∠BDE=80°.
∵四边形ADEC是以AE为对称轴的轴对称图形,
∴AD=EC,DE=DC,∠ADE=∠C=80°.
在△ABC中,∠BAC=180°-∠B-∠C=180°-40°-80°=60°.
故∠BAC的度数为60°.
∵BD=DE,∠B=40°,
∴∠BED=∠B=40°,
∴∠BDE=180°-∠B-∠BED=100°,
∴∠ADE=180°-∠BDE=80°.
∵四边形ADEC是以AE为对称轴的轴对称图形,
∴AD=EC,DE=DC,∠ADE=∠C=80°.
在△ABC中,∠BAC=180°-∠B-∠C=180°-40°-80°=60°.
故∠BAC的度数为60°.
例3 如图1,小强拿了一张正方形的纸,沿虚线对折一次得图2,再对折一次得图3,然后用剪刀沿图3中的虚线(虚线与底边不平行)剪去一个角,再打开后的形状应是 (
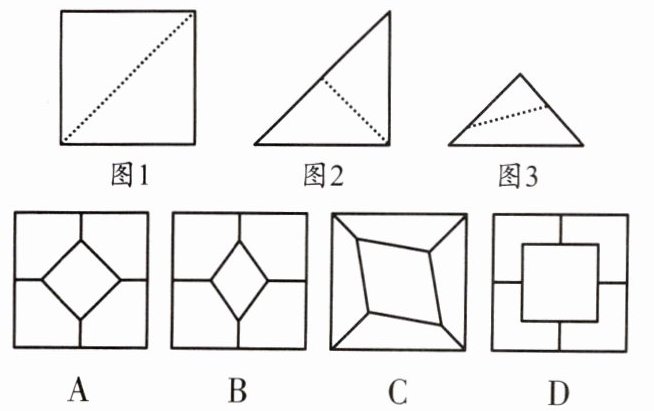
分析:从图3来看,剪痕应与正方形的对角线有交点,故不难得出答案C正确.
归纳:
此类题可以动手剪一剪,也可以利用对称知识将最后一幅图逐次对称回去,从而得到原图案或形状.
C
)
分析:从图3来看,剪痕应与正方形的对角线有交点,故不难得出答案C正确.
归纳:
此类题可以动手剪一剪,也可以利用对称知识将最后一幅图逐次对称回去,从而得到原图案或形状.
答案:
【解析】:
首先,我们分析题目中的折叠和剪切过程。
从图1到图2,是沿正方形的对角线折叠一次,得到一个等腰直角三角形。
从图2到图3,是再次沿等腰直角三角形的对称轴(也就是高)折叠一次,得到一个更小的等腰直角三角形。
在图3中,虚线(剪切线)与底边不平行,且与等腰直角三角形的斜边(原正方形的对角线)有交点。
接下来,我们考虑剪切后的形状。
由于剪切线不与底边平行,且与对角线有交点,因此剪去一个角后,打开的形状将不再是一个规则的多边形,但会保留对称性。
现在,我们逐一分析选项:
A选项:形状不符合剪切后的对称性。
B选项:同样不符合剪切后的形状和对称性。
C选项:这个形状符合我们之前的分析,即剪去一个角后,由于剪切线与对角线有交点,打开的形状会保留对称性,并且四个角都进行了裁剪,形成类似菱形的形状但四边并不相等,而是由两对相等的边组成,形成“回”字上下部分底边拉长的变形,符合题意。
D选项:形状明显与剪切后的形状不符。
综上所述,再打开后的形状应是C选项。
【答案】:C。
首先,我们分析题目中的折叠和剪切过程。
从图1到图2,是沿正方形的对角线折叠一次,得到一个等腰直角三角形。
从图2到图3,是再次沿等腰直角三角形的对称轴(也就是高)折叠一次,得到一个更小的等腰直角三角形。
在图3中,虚线(剪切线)与底边不平行,且与等腰直角三角形的斜边(原正方形的对角线)有交点。
接下来,我们考虑剪切后的形状。
由于剪切线不与底边平行,且与对角线有交点,因此剪去一个角后,打开的形状将不再是一个规则的多边形,但会保留对称性。
现在,我们逐一分析选项:
A选项:形状不符合剪切后的对称性。
B选项:同样不符合剪切后的形状和对称性。
C选项:这个形状符合我们之前的分析,即剪去一个角后,由于剪切线与对角线有交点,打开的形状会保留对称性,并且四个角都进行了裁剪,形成类似菱形的形状但四边并不相等,而是由两对相等的边组成,形成“回”字上下部分底边拉长的变形,符合题意。
D选项:形状明显与剪切后的形状不符。
综上所述,再打开后的形状应是C选项。
【答案】:C。
查看更多完整答案,请扫码查看


