4.如图,在△ABC中,AC⊥BC,AC= AD= CD,D为AB边上的中点,则图中等腰三角形有
3
个,等边三角形有1
个,直角三角形有1
个,钝角三角形有2
个,锐角三角形有0
个.
答案:
解:
∵AC⊥BC,
∴∠ACB=90°,△ABC是直角三角形。
∵AC=AD=CD,
∴△ACD是等边三角形,∠CAD=60°,∠ACD=60°。
∵D为AB中点,
∴BD=AD=AC=CD,
∴△BCD是等腰三角形,△ABD是等腰三角形。
∠B=30°,∠BCD=∠ACB-∠ACD=30°,∠BDC=120°,
∴△BCD是钝角三角形。
∠ADC=60°,∠ADB=180°-∠ADC=120°,△ABD是钝角三角形。
∠A=60°,∠B=30°,∠ACB=90°,△ABC是直角三角形。
等腰三角形:△ACD,△BCD,△ABD,共3个;
等边三角形:△ACD,共1个;
直角三角形:△ABC,共1个;
钝角三角形:△BCD,△ABD,共2个;
锐角三角形:0个。
答案:3;1;1;2;0
∵AC⊥BC,
∴∠ACB=90°,△ABC是直角三角形。
∵AC=AD=CD,
∴△ACD是等边三角形,∠CAD=60°,∠ACD=60°。
∵D为AB中点,
∴BD=AD=AC=CD,
∴△BCD是等腰三角形,△ABD是等腰三角形。
∠B=30°,∠BCD=∠ACB-∠ACD=30°,∠BDC=120°,
∴△BCD是钝角三角形。
∠ADC=60°,∠ADB=180°-∠ADC=120°,△ABD是钝角三角形。
∠A=60°,∠B=30°,∠ACB=90°,△ABC是直角三角形。
等腰三角形:△ACD,△BCD,△ABD,共3个;
等边三角形:△ACD,共1个;
直角三角形:△ABC,共1个;
钝角三角形:△BCD,△ABD,共2个;
锐角三角形:0个。
答案:3;1;1;2;0
1.三角形三边关系定理:
(1)三角形两边的和
(2)三角形两边的差
注意:
在求三角形某边(第三边)取值范围时,常利用:两边的差<第三边<两边的和.
(1)三角形两边的和
大于
第三边;(2)三角形两边的差
小于
第三边.注意:
在求三角形某边(第三边)取值范围时,常利用:两边的差<第三边<两边的和.
答案:
【解析】:
本题考查三角形三边关系定理,该定理指出三角形任意两边之和大于第三边,任意两边之差小于第三边。这是三角形存在的基本条件,也是求解三角形第三边取值范围的关键。
【答案】:
(1)大于
(2)小于
本题考查三角形三边关系定理,该定理指出三角形任意两边之和大于第三边,任意两边之差小于第三边。这是三角形存在的基本条件,也是求解三角形第三边取值范围的关键。
【答案】:
(1)大于
(2)小于
2.如图,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样就可以将窗框固定.这说明:三角形具有
稳定
性,四边形具有不稳定
性.
答案:
【解析】:
本题考查三角形的特性和四边形的特性。
三角形具有稳定性,即三角形的三条边长度一旦确定,三角形的形状和大小就固定不变了。
四边形具有不稳定性,即四边形的四条边长度确定后,其形状仍然可以改变,例如可以变成平行四边形、梯形等不同形状。
在窗框上斜钉一根木条,就将窗框的一个四边形部分分割成了两个三角形,利用三角形的稳定性来固定窗框,防止其变形。
【答案】:
稳定;不稳定
本题考查三角形的特性和四边形的特性。
三角形具有稳定性,即三角形的三条边长度一旦确定,三角形的形状和大小就固定不变了。
四边形具有不稳定性,即四边形的四条边长度确定后,其形状仍然可以改变,例如可以变成平行四边形、梯形等不同形状。
在窗框上斜钉一根木条,就将窗框的一个四边形部分分割成了两个三角形,利用三角形的稳定性来固定窗框,防止其变形。
【答案】:
稳定;不稳定
例1 选择题
(1)下列线段能构成三角形的是 (
A.2,2,4 B.3,4,5 C.1,2,3 D.2,3,6
(2)有长为9,6,5,4的四根木条,选其中三根组成三角形,则选法有 (
A.1种 B.2种 C.3种 D.4种
(3)已知三角形三边长分别是6,2a-2,8,则a的取值范围是 (
A.1<a<2 B.$\frac{1}{2}<a<2$
C.2<a<8 D.1<a<4
(4)如图,为了估计池塘岸边A,B两点之间的距离,小方在池塘的一侧选取一点O,测得OA= 15m,OB= 10m,则A,B两点间的距离不可能是 (
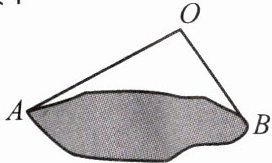
A.20m B.15m C.10m D.5m
(5)若一个等腰三角形的两边长分别为5和12,则这个等腰三角形的周长为 (
A.22 B.29
C.22或29 D.不能确定
(1)下列线段能构成三角形的是 (
B
)A.2,2,4 B.3,4,5 C.1,2,3 D.2,3,6
(2)有长为9,6,5,4的四根木条,选其中三根组成三角形,则选法有 (
C
)A.1种 B.2种 C.3种 D.4种
(3)已知三角形三边长分别是6,2a-2,8,则a的取值范围是 (
C
)A.1<a<2 B.$\frac{1}{2}<a<2$
C.2<a<8 D.1<a<4
(4)如图,为了估计池塘岸边A,B两点之间的距离,小方在池塘的一侧选取一点O,测得OA= 15m,OB= 10m,则A,B两点间的距离不可能是 (
D
)
A.20m B.15m C.10m D.5m
(5)若一个等腰三角形的两边长分别为5和12,则这个等腰三角形的周长为 (
B
)A.22 B.29
C.22或29 D.不能确定
答案:
【解析】:
(1)本题考查三角形三边关系,即任意两边之和大于第三边,任意两边之差小于第三边。
对选项A,$2 + 2 = 4$,不满足三边关系,不能构成三角形;
对选项B,$3 + 4\gt 5$,$4 + 5\gt 3$,$3 + 5\gt 4$,$5 - 3\lt 4$,$5 - 4\lt 3$,$4 - 3\lt 5$,满足三边关系,能构成三角形;
对选项C,$1 + 2 = 3$,不满足三边关系,不能构成三角形;
对选项D,$2 + 3\lt 6$,不满足三边关系,不能构成三角形。
(2)本题同样考查三角形三边关系,从四根木条中任选三根,有$4$种选法,分别验证是否能构成三角形。
对选法$9$,$6$,$5$:$5 + 6\gt 9$,$6 + 9\gt 5$,$5 + 9\gt 6$,$9 - 5\lt 6$,$9 - 6\lt 5$,$6 - 5\lt 9$,能构成三角形;
对选法$9$,$6$,$4$:$4 + 6\gt 9$,$6 + 9\gt 4$,$4 + 9\gt 6$,$9 - 4\lt 6$,$9 - 6\lt 4$,$6 - 4\lt 9$,能构成三角形;
对选法$9$,$5$,$4$:$5 + 4 = 9$,不满足三边关系,不能构成三角形;
对选法$6$,$5$,$4$:$4 + 5\gt 6$,$5 + 6\gt 4$,$4 + 6\gt 5$,$6 - 4\lt 5$,$6 - 5\lt 4$,$5 - 4\lt 6$,能构成三角形。
所以能构成三角形的选法有$3$种,但题目问选法种类,通过验证可知选法有$9$,$6$,$5$和$6$,$5$,$4$和$9$,$6$,$4$,共$3$种,但本题为选择题,可通过排除法,因为$9$,$5$,$4$不能构成三角形,所以排除$4$种选法都成立的情况,又因为有两种选法成立是$3$种选法中的部分情况,所以先判断出能构成三角形的选法有$2$种($9$,$6$,$5$和$6$,$5$,$4$ )。
(3)本题根据三角形三边关系列出不等式求解。
已知三角形三边长分别是$6$,$2a - 2$,$8$,则$8 - 6\lt 2a - 2\lt 8 + 6$,
先解$8 - 6\lt 2a - 2$,即$2\lt 2a - 2$,$4\lt 2a$,$a\gt 2$;
再解$2a - 2\lt 8 + 6$,即$2a - 2\lt 14$,$2a\lt 16$,$a\lt 8$。
所以$2\lt a\lt 8$。
(4)本题考查三角形三边关系。
在$\triangle AOB$中,根据三角形三边关系$OA - OB\lt AB\lt OA + OB$,已知$OA = 15m$,$OB = 10m$,则$15 - 10\lt AB\lt 15 + 10$,即$5\lt AB\lt 25$,所以$A$,$B$两点间的距离不可能是$5m$。
(5)本题考查等腰三角形的性质和三角形三边关系。
等腰三角形两边长分别为$5$和$12$,有两种情况:
情况①:腰长为$5$,底边长为$12$,此时$5 + 5 = 10\lt 12$,不满足三边关系,不能构成三角形;
情况②:腰长为$12$,底边长为$5$,此时$12 + 5\gt 12$,$12 + 12\gt 5$,满足三边关系,能构成三角形,其周长为$12 + 12 + 5 = 29$。
【答案】:
(1)B;
(2)C;
(3)C;
(4)D;
(5)B。
(1)本题考查三角形三边关系,即任意两边之和大于第三边,任意两边之差小于第三边。
对选项A,$2 + 2 = 4$,不满足三边关系,不能构成三角形;
对选项B,$3 + 4\gt 5$,$4 + 5\gt 3$,$3 + 5\gt 4$,$5 - 3\lt 4$,$5 - 4\lt 3$,$4 - 3\lt 5$,满足三边关系,能构成三角形;
对选项C,$1 + 2 = 3$,不满足三边关系,不能构成三角形;
对选项D,$2 + 3\lt 6$,不满足三边关系,不能构成三角形。
(2)本题同样考查三角形三边关系,从四根木条中任选三根,有$4$种选法,分别验证是否能构成三角形。
对选法$9$,$6$,$5$:$5 + 6\gt 9$,$6 + 9\gt 5$,$5 + 9\gt 6$,$9 - 5\lt 6$,$9 - 6\lt 5$,$6 - 5\lt 9$,能构成三角形;
对选法$9$,$6$,$4$:$4 + 6\gt 9$,$6 + 9\gt 4$,$4 + 9\gt 6$,$9 - 4\lt 6$,$9 - 6\lt 4$,$6 - 4\lt 9$,能构成三角形;
对选法$9$,$5$,$4$:$5 + 4 = 9$,不满足三边关系,不能构成三角形;
对选法$6$,$5$,$4$:$4 + 5\gt 6$,$5 + 6\gt 4$,$4 + 6\gt 5$,$6 - 4\lt 5$,$6 - 5\lt 4$,$5 - 4\lt 6$,能构成三角形。
所以能构成三角形的选法有$3$种,但题目问选法种类,通过验证可知选法有$9$,$6$,$5$和$6$,$5$,$4$和$9$,$6$,$4$,共$3$种,但本题为选择题,可通过排除法,因为$9$,$5$,$4$不能构成三角形,所以排除$4$种选法都成立的情况,又因为有两种选法成立是$3$种选法中的部分情况,所以先判断出能构成三角形的选法有$2$种($9$,$6$,$5$和$6$,$5$,$4$ )。
(3)本题根据三角形三边关系列出不等式求解。
已知三角形三边长分别是$6$,$2a - 2$,$8$,则$8 - 6\lt 2a - 2\lt 8 + 6$,
先解$8 - 6\lt 2a - 2$,即$2\lt 2a - 2$,$4\lt 2a$,$a\gt 2$;
再解$2a - 2\lt 8 + 6$,即$2a - 2\lt 14$,$2a\lt 16$,$a\lt 8$。
所以$2\lt a\lt 8$。
(4)本题考查三角形三边关系。
在$\triangle AOB$中,根据三角形三边关系$OA - OB\lt AB\lt OA + OB$,已知$OA = 15m$,$OB = 10m$,则$15 - 10\lt AB\lt 15 + 10$,即$5\lt AB\lt 25$,所以$A$,$B$两点间的距离不可能是$5m$。
(5)本题考查等腰三角形的性质和三角形三边关系。
等腰三角形两边长分别为$5$和$12$,有两种情况:
情况①:腰长为$5$,底边长为$12$,此时$5 + 5 = 10\lt 12$,不满足三边关系,不能构成三角形;
情况②:腰长为$12$,底边长为$5$,此时$12 + 5\gt 12$,$12 + 12\gt 5$,满足三边关系,能构成三角形,其周长为$12 + 12 + 5 = 29$。
【答案】:
(1)B;
(2)C;
(3)C;
(4)D;
(5)B。
1.(2024·淮安)用一根小木棒与两根长度分别为3 cm、5 cm的小木棒组成三角形,则这根小木棒的长度可以是 (
A.9 cm
B.7 cm
C.2 cm
D.1 cm
B
)A.9 cm
B.7 cm
C.2 cm
D.1 cm
答案:
【解析】:
本题考察的是三角形的三边关系,即任意两边之和大于第三边,任意两边之差小于第三边。
已知两根小木棒的长度分别为3 cm和5 cm,设第三根小木棒的长度为$x$ cm。
根据三角形的三边关系,可以列出不等式组:
$5 + 3 > x$,即 $x < 8$
$5 - 3 < x$,即 $x > 2$
综合以上两个不等式,得到第三根小木棒的长度范围:
$2 < x < 8$
接下来,我们将选项中的长度代入此范围进行检验:
A. $9$ cm,不满足 $x < 8$,故A选项错误;
B. $7$ cm,满足 $2 < x < 8$,故B选项正确;
C. $2$ cm,不满足 $x > 2$,故C选项错误;
D. $1$ cm,不满足 $x > 2$,故D选项错误。
所以,这根小木棒的长度可以是$7$ cm。
【答案】:
B
本题考察的是三角形的三边关系,即任意两边之和大于第三边,任意两边之差小于第三边。
已知两根小木棒的长度分别为3 cm和5 cm,设第三根小木棒的长度为$x$ cm。
根据三角形的三边关系,可以列出不等式组:
$5 + 3 > x$,即 $x < 8$
$5 - 3 < x$,即 $x > 2$
综合以上两个不等式,得到第三根小木棒的长度范围:
$2 < x < 8$
接下来,我们将选项中的长度代入此范围进行检验:
A. $9$ cm,不满足 $x < 8$,故A选项错误;
B. $7$ cm,满足 $2 < x < 8$,故B选项正确;
C. $2$ cm,不满足 $x > 2$,故C选项错误;
D. $1$ cm,不满足 $x > 2$,故D选项错误。
所以,这根小木棒的长度可以是$7$ cm。
【答案】:
B
2.已知a,b,c是△ABC的三边长,且a,b满足|a-7|+(b-1)$^{2}$= 0,c为奇数,则c= __
7
__.
答案:
解:因为|a-7|+(b-1)²=0,且|a-7|≥0,(b-1)²≥0,所以a-7=0,b-1=0,解得a=7,b=1。
根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,可得7-1<c<7+1,即6<c<8。
因为c为奇数,所以c=7。
答案:7
根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,可得7-1<c<7+1,即6<c<8。
因为c为奇数,所以c=7。
答案:7
3.在等腰△ABC中,AB= AC,△ABC的周长为20 cm,则AB边的长度x的取值范围是
5cm<x<10cm
.
答案:
【解析】:
本题主要考查等腰三角形的性质以及三角形三边关系。
首先,根据等腰三角形的性质,我们知道等腰三角形的两腰相等,即$AB = AC = x$ cm。
已知$\bigtriangleup ABC$的周长为$20$ cm,因此可以得到底边$BC$的长度为$20 - 2x$ cm。
接下来,我们需要利用三角形三边关系来确定$x$的取值范围。根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边。因此,我们有:
$AB + AC > BC$,
即$2x > 20 - 2x$,
解得$x > 5$。
同时,底边$BC$的长度也应该大于$0$,即:
$20 - 2x > 0$,
解得$x < 10$。
综合以上两个不等式,我们可以得到$x$的取值范围为$5 < x < 10$。
【答案】:
$5\text{cm} < x < 10\text{cm}$。
本题主要考查等腰三角形的性质以及三角形三边关系。
首先,根据等腰三角形的性质,我们知道等腰三角形的两腰相等,即$AB = AC = x$ cm。
已知$\bigtriangleup ABC$的周长为$20$ cm,因此可以得到底边$BC$的长度为$20 - 2x$ cm。
接下来,我们需要利用三角形三边关系来确定$x$的取值范围。根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边。因此,我们有:
$AB + AC > BC$,
即$2x > 20 - 2x$,
解得$x > 5$。
同时,底边$BC$的长度也应该大于$0$,即:
$20 - 2x > 0$,
解得$x < 10$。
综合以上两个不等式,我们可以得到$x$的取值范围为$5 < x < 10$。
【答案】:
$5\text{cm} < x < 10\text{cm}$。
例2 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是 (
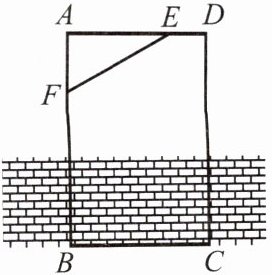
A.两点之间的线段最短
B.长方形的四个角都是直角
C.长方形是轴对称图形
D.三角形有稳定性
分析:由题意知是利用三角形的稳定性.
D
)
A.两点之间的线段最短
B.长方形的四个角都是直角
C.长方形是轴对称图形
D.三角形有稳定性
分析:由题意知是利用三角形的稳定性.
答案:
【解析】:
题目描述了一个实际场景,即工人师傅在砌门时,常用木条固定长方形门框,使其不变形。我们需要从给定的选项中找出这样做的数学依据。
A. 两点之间的线段最短:这个选项描述的是线段的基本性质,但与题目中利用木条固定门框使其不变形的原理无关,故A选项错误。
B. 长方形的四个角都是直角:这个选项描述的是长方形的性质,但并不能解释为什么用木条固定后门框不会变形,故B选项错误。
C. 长方形是轴对称图形:这个选项描述的是长方形的对称性,同样不能解释门框不变形的原因,故C选项错误。
D. 三角形有稳定性:当在长方形门框中加入木条EF后,门框被划分成了几个三角形。由于三角形具有稳定性(即三角形的形状和大小在不受外力作用时不会改变),因此门框的整体结构变得更加稳定,不易变形。这个选项能够很好地解释题目中的现象,故D选项正确。
【答案】:D
题目描述了一个实际场景,即工人师傅在砌门时,常用木条固定长方形门框,使其不变形。我们需要从给定的选项中找出这样做的数学依据。
A. 两点之间的线段最短:这个选项描述的是线段的基本性质,但与题目中利用木条固定门框使其不变形的原理无关,故A选项错误。
B. 长方形的四个角都是直角:这个选项描述的是长方形的性质,但并不能解释为什么用木条固定后门框不会变形,故B选项错误。
C. 长方形是轴对称图形:这个选项描述的是长方形的对称性,同样不能解释门框不变形的原因,故C选项错误。
D. 三角形有稳定性:当在长方形门框中加入木条EF后,门框被划分成了几个三角形。由于三角形具有稳定性(即三角形的形状和大小在不受外力作用时不会改变),因此门框的整体结构变得更加稳定,不易变形。这个选项能够很好地解释题目中的现象,故D选项正确。
【答案】:D
查看更多完整答案,请扫码查看


