《2025年巅峰对决八年级数学上册人教版》

3. 如图,AD是△ABC的高,AD= BD,DE= DC,∠AEB= 120°,则∠C= ______.
60°

答案： 证明：
∵AD是△ABC的高，
∴∠ADB=∠ADC=90°。
在△BDE和△ADC中，
BD=AD，
∠BDE=∠ADC=90°，
DE=DC，
∴△BDE≌△ADC（SAS）。
∴∠BED=∠C。
∵∠AEB=120°，∠AEB+∠BED=180°，
∴∠BED=180°-∠AEB=60°。
∴∠C=∠BED=60°。
60°

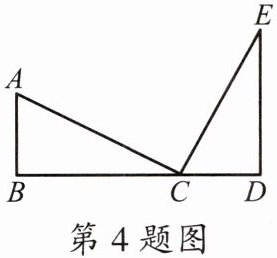
4. 如图,已知AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB= CD,BC= DE,则∠ACE= ______.

90°

答案： 证明：
∵AB⊥BD，ED⊥BD，
∴∠B=∠D=90°。
在△ABC和△CDE中，
AB=CD（已知），
∠B=∠D（已证），
BC=DE（已知），
∴△ABC≌△CDE（SAS）。
∴∠A=∠ECD，∠ACB=∠E。
∵∠A+∠ACB=90°（直角三角形两锐角互余），
∴∠ECD+∠ACB=90°。
∵点B，C，D在同一直线上，
∴∠ACB+∠ACE+∠ECD=180°，
∴∠ACE=180°-（∠ACB+∠ECD）=180°-90°=90°。
90°

5. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2= ______.

90°

答案： 证明：设每个小正方形边长为1。
在网格中取∠1所在三角形，两直角边分别为2、4；∠2所在三角形，两直角边分别为1、2。
∵2/1=4/2=2，且两三角形均为直角三角形，
∴两直角三角形相似。
∴∠1的对应角与∠2互余，即∠1+∠2=90°。
90°

1. 三角形全等的基本事实:两角和它们的 夹边 分别相等的两个三角形全等(可以简写成"角边角"或"ASA").
符号语言:
在△ABC 和△DEF 中,

∵∠A= ∠D,
AB= DE,
∠B= ∠E,
∴△ABC≌△DEF(ASA).
2. 三角形全等的基本事实:两角分别 相等 且其中一组等角的 对边 相等的两个三角形全等(可以简写成"角角边"或"AAS").
符号语言:
在△ABC 和△DEF 中,

∵∠A= ∠D,
∠B= ∠E,
BC= EF,
∴△ABC≌△DEF(AAS).

答案：

例1 如图,∠1= ∠2,∠3= ∠4,求证:AC= AD.
分析:先证出∠ABC= ∠ABD,再由 ASA 证明△ABC≌△ABD,得出对应边相等即可.

答案： 【解析】：
本题考查了全等三角形的判定与性质。根据已知条件$\angle 1=\angle 2$，$\angle 3=\angle 4$以及公共边$AB=AB$，可以利用角边角（$ASA$）判定定理来证明$\triangle ABC\cong\triangle ABD$，从而得出对应边$AC=AD$。
【答案】：
证明：
∵$\angle 3=\angle 4$，
∴$\angle ABC=\angle ABD$，
在$\triangle ABC$和$\triangle ABD$中，
$\left\{\begin{matrix}\angle 1=\angle 2,\\AB=AB,\\\angle ABC=\angle ABD.\end{matrix}\right.$
∴$\triangle ABC\cong\triangle ABD(ASA)$，
∴$AC=AD$。

1. 如图,D 是 AB 上一点,DF 交 AC 于点 E,DE= FE,FC//AB.若 AB= 4,CF= 3,则 BD 的长是 (B)

A.0.5
B.1
C.1.5
D.2

答案： 证明：
∵FC//AB，
∴∠ADE=∠CFE（两直线平行，内错角相等）。
在△ADE和△CFE中，
∠ADE=∠CFE，
DE=FE，
∠AED=∠CEF（对顶角相等），
∴△ADE≌△CFE（ASA）。
∴AD=CF=3（全等三角形对应边相等）。
∵AB=4，
∴BD=AB-AD=4-3=1。
答案：B

2. 如图,点 D 在 AB 上,点 E 在 AC 上,AB= AC,∠B= ∠C,求证:AD= AE.

答案： 【解析】：本题考查全等三角形的证明，根据题目已知条件$AB= AC$，$∠B= ∠C$以及$∠A$为公共角，我们可以利用“ASA”判定定理来证明$△ABE$和$△ACD$全等，进而得出$AD= AE$。
【答案】： 证明：
在$△ABE$和$△ACD$中，
$\left\{\begin{matrix}∠A=∠A,\\AB=AC,\\∠B=∠C.\end{matrix}\right.$
根据全等三角形的“ASA”判定定理，
∴$△ABE\cong△ACD$，
∴$AD=AE$。