5.如图,BD平分∠ABC,CD平分∠ACB.若∠A= 80°,则∠D的度数为(

A.100°
B.120°
C.130°
D.140°
C
)
A.100°
B.120°
C.130°
D.140°
答案:
【解析】:本题可根据三角形内角和定理以及角平分线的性质来求解$\angle D$的度数。
步骤一:明确三角形内角和定理
三角形内角和定理为:三角形的内角和等于$180^{\circ}$,即在$\triangle ABC$中,$\angle A + \angle ABC + \angle ACB = 180^{\circ}$。
已知$\angle A = 80^{\circ}$,将其代入上式可得$\angle ABC + \angle ACB = 180^{\circ} - \angle A = 180^{\circ} - 80^{\circ} = 100^{\circ}$。
步骤二:根据角平分线的性质求出$\angle DBC + \angle DCB$的度数
因为$BD$平分$\angle ABC$,$CD$平分$\angle ACB$,根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线。
所以$\angle DBC = \frac{1}{2}\angle ABC$,$\angle DCB = \frac{1}{2}\angle ACB$。
则$\angle DBC + \angle DCB = \frac{1}{2}(\angle ABC + \angle ACB)$,将$\angle ABC + \angle ACB = 100^{\circ}$代入可得:
$\angle DBC + \angle DCB = \frac{1}{2}×100^{\circ} = 50^{\circ}$。
步骤三:在$\triangle BDC$中求出$\angle D$的度数
在$\triangle BDC$中,根据三角形内角和定理可得$\angle D + \angle DBC + \angle DCB = 180^{\circ}$。
将$\angle DBC + \angle DCB = 50^{\circ}$代入上式可得:
$\angle D = 180^{\circ} - (\angle DBC + \angle DCB) = 180^{\circ} - 50^{\circ} = 130^{\circ}$。
【答案】:C
步骤一:明确三角形内角和定理
三角形内角和定理为:三角形的内角和等于$180^{\circ}$,即在$\triangle ABC$中,$\angle A + \angle ABC + \angle ACB = 180^{\circ}$。
已知$\angle A = 80^{\circ}$,将其代入上式可得$\angle ABC + \angle ACB = 180^{\circ} - \angle A = 180^{\circ} - 80^{\circ} = 100^{\circ}$。
步骤二:根据角平分线的性质求出$\angle DBC + \angle DCB$的度数
因为$BD$平分$\angle ABC$,$CD$平分$\angle ACB$,根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线。
所以$\angle DBC = \frac{1}{2}\angle ABC$,$\angle DCB = \frac{1}{2}\angle ACB$。
则$\angle DBC + \angle DCB = \frac{1}{2}(\angle ABC + \angle ACB)$,将$\angle ABC + \angle ACB = 100^{\circ}$代入可得:
$\angle DBC + \angle DCB = \frac{1}{2}×100^{\circ} = 50^{\circ}$。
步骤三:在$\triangle BDC$中求出$\angle D$的度数
在$\triangle BDC$中,根据三角形内角和定理可得$\angle D + \angle DBC + \angle DCB = 180^{\circ}$。
将$\angle DBC + \angle DCB = 50^{\circ}$代入上式可得:
$\angle D = 180^{\circ} - (\angle DBC + \angle DCB) = 180^{\circ} - 50^{\circ} = 130^{\circ}$。
【答案】:C
6.(2023·徐州)如图,在△ABC中,若DE//BC,FG//AC,∠BDE= 120°,∠DFG= 115°,则∠C= ______
55°
.
答案:
【解析】:本题可根据平行线的性质求出$\angle ABC$与$\angle BDF$的度数,再利用三角形外角的性质求出$\angle C$的度数。
步骤一:根据平行线的性质求出$\angle ABC$的度数
已知$DE// BC$,$\angle BDE = 120^{\circ}$。
因为两直线平行,同旁内角互补,所以$\angle ABC$与$\angle BDE$互补,即$\angle ABC + \angle BDE = 180^{\circ}$。
将$\angle BDE = 120^{\circ}$代入上式可得:$\angle ABC = 180^{\circ} - 120^{\circ} = 60^{\circ}$。
步骤二:根据平行线的性质求出$\angle BDF$的度数
已知$FG// AC$,$\angle DFG = 115^{\circ}$。
因为两直线平行,同位角相等,所以$\angle BDF$与$\angle DFG$相等,即$\angle BDF = \angle DFG = 115^{\circ}$。
步骤三:根据三角形外角的性质求出$\angle C$的度数
在$\triangle BDF$中,$\angle BDF$是外角,根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,可得$\angle BDF = \angle ABC + \angle C$。
将$\angle ABC = 60^{\circ}$,$\angle BDF = 115^{\circ}$代入上式可得:$115^{\circ} = 60^{\circ} + \angle C$。
移项可得:$\angle C = 115^{\circ} - 60^{\circ} = 55^{\circ}$。
【答案】:$55^{\circ}$
步骤一:根据平行线的性质求出$\angle ABC$的度数
已知$DE// BC$,$\angle BDE = 120^{\circ}$。
因为两直线平行,同旁内角互补,所以$\angle ABC$与$\angle BDE$互补,即$\angle ABC + \angle BDE = 180^{\circ}$。
将$\angle BDE = 120^{\circ}$代入上式可得:$\angle ABC = 180^{\circ} - 120^{\circ} = 60^{\circ}$。
步骤二:根据平行线的性质求出$\angle BDF$的度数
已知$FG// AC$,$\angle DFG = 115^{\circ}$。
因为两直线平行,同位角相等,所以$\angle BDF$与$\angle DFG$相等,即$\angle BDF = \angle DFG = 115^{\circ}$。
步骤三:根据三角形外角的性质求出$\angle C$的度数
在$\triangle BDF$中,$\angle BDF$是外角,根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,可得$\angle BDF = \angle ABC + \angle C$。
将$\angle ABC = 60^{\circ}$,$\angle BDF = 115^{\circ}$代入上式可得:$115^{\circ} = 60^{\circ} + \angle C$。
移项可得:$\angle C = 115^{\circ} - 60^{\circ} = 55^{\circ}$。
【答案】:$55^{\circ}$
1.三角形的外角定义:三角形的一边与另一边的延长线组成的角,叫作
注意:
三角形一共有6个外角,且每个顶点处的两个外角互为对顶角.
三角形的外角
.注意:
三角形一共有6个外角,且每个顶点处的两个外角互为对顶角.
答案:
【解析】:
这道题目考查的是三角形外角的定义。根据题目描述和八年级数学人教版上册的相关内容,我们可以知道三角形的一边与另一边的延长线组成的角被称作三角形的外角。同时,三角形每个顶点处都有两个外角,这两个外角是互为对顶角的。
【答案】:
三角形的外角
这道题目考查的是三角形外角的定义。根据题目描述和八年级数学人教版上册的相关内容,我们可以知道三角形的一边与另一边的延长线组成的角被称作三角形的外角。同时,三角形每个顶点处都有两个外角,这两个外角是互为对顶角的。
【答案】:
三角形的外角
2.三角形内角和定理推论:三角形的外角等于与它
符号语言:如图,
∵∠ACD是△ABC的外角,
∴∠ACD= ∠A+∠B.
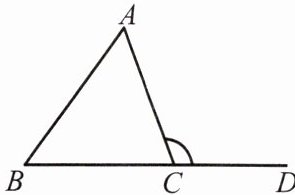
注意:
由推论易知:三角形的外角大于任一与它不相邻的内角.
不相邻
的两个内角的和.符号语言:如图,
∵∠ACD是△ABC的外角,
∴∠ACD= ∠A+∠B.

注意:
由推论易知:三角形的外角大于任一与它不相邻的内角.
答案:
【解析】:本题考查三角形内角和定理的推论,即三角形的外角性质。
根据三角形外角的性质,三角形的外角等于与它不相邻的两个内角的和。
在本题的图中,∠ACD是△ABC的一个外角,
因此,∠ACD等于与它不相邻的两个内角∠A和∠B的和。
同时,由这个推论可以得知,三角形的外角大于任一与它不相邻的内角。
【答案】:不相邻
根据三角形外角的性质,三角形的外角等于与它不相邻的两个内角的和。
在本题的图中,∠ACD是△ABC的一个外角,
因此,∠ACD等于与它不相邻的两个内角∠A和∠B的和。
同时,由这个推论可以得知,三角形的外角大于任一与它不相邻的内角。
【答案】:不相邻
3.三角形的外角和为
$360^\circ$
.
答案:
【解析】:
本题考查的是三角形外角和的知识点。根据三角形外角和的定义和性质,我们知道三角形的每个外角与其相邻的内角是补角,而三角形的内角和为$180^\circ$。由于一个外角与其相邻的内角之和为$180^\circ$,三角形有三个外角,每个外角都等于$180^\circ$减去相邻的内角。但考虑到三角形的内角和为$180^\circ$,因此三个外角的和为$360^\circ$(因为每个外角都“占据”了$180^\circ$的一部分,而三角形的内角被算了两次“占据”,所以总和为$3 × 180^\circ - 180^\circ × 2 = 360^\circ$,或者更直观地,每个外角都“延伸”出三角形的一个顶点,形成了围绕三角形的一个完整圆周,即$360^\circ$)。
【答案】:
$360^\circ$
本题考查的是三角形外角和的知识点。根据三角形外角和的定义和性质,我们知道三角形的每个外角与其相邻的内角是补角,而三角形的内角和为$180^\circ$。由于一个外角与其相邻的内角之和为$180^\circ$,三角形有三个外角,每个外角都等于$180^\circ$减去相邻的内角。但考虑到三角形的内角和为$180^\circ$,因此三个外角的和为$360^\circ$(因为每个外角都“占据”了$180^\circ$的一部分,而三角形的内角被算了两次“占据”,所以总和为$3 × 180^\circ - 180^\circ × 2 = 360^\circ$,或者更直观地,每个外角都“延伸”出三角形的一个顶点,形成了围绕三角形的一个完整圆周,即$360^\circ$)。
【答案】:
$360^\circ$
例1 如图,在△ABC中,∠A= ∠ABD,∠ABC= ∠ACB= ∠BDC,求∠A的度数.
分析:可设∠A= x,从而用含x的式子表示出∠ABC及∠ACB,再由∠A+∠ABC+∠ACB= 180°解出x即得.
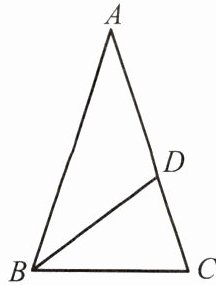
归纳:
对于图形中多个角之间有相互关系时,常设较小角为x,其他角尽量用含x的式子表示,进而利用三角形的内角和为180°建立方程求解.
分析:可设∠A= x,从而用含x的式子表示出∠ABC及∠ACB,再由∠A+∠ABC+∠ACB= 180°解出x即得.
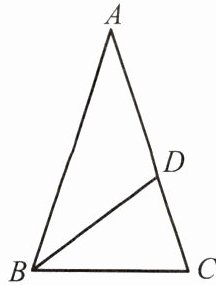
归纳:
对于图形中多个角之间有相互关系时,常设较小角为x,其他角尽量用含x的式子表示,进而利用三角形的内角和为180°建立方程求解.
答案:
【解析】:本题考查了三角形内角和定理的应用,设$\angle A=x$,根据题目中的角度关系,表示出$\angle ABC$和$\angle ACB$,再利用三角形内角和定理列出方程,进而求解$\angle A$的度数。
设$\angle A=x$,
因为$\angle A = \angle ABD$,所以$\angle ABD = x$。
设$\angle ABC = \angle ACB = \angle BDC = y$,
在$\triangle ABD$中,根据三角形外角性质,$\angle BDC$是$\triangle ABD$的一个外角,
所以$\angle BDC=\angle A + \angle ABD$,即$y = x + x = 2x$。
因为$\angle ABC = \angle ACB = y$,而$y = 2x$,
所以在$\triangle ABC$中,$\angle ABC = \angle ACB = 2x$。
在$\triangle ABC$中,根据三角形内角和定理,$\angle A + \angle ABC + \angle ACB = 180^{\circ}$,
即$x + 2x + 2x = 180^{\circ}$。
合并同类项可得$5x = 180^{\circ}$,
解得$x = 36^{\circ}$,即$\angle A = 36^{\circ}$。
【答案】:$\angle A = 36^{\circ}$。
设$\angle A=x$,
因为$\angle A = \angle ABD$,所以$\angle ABD = x$。
设$\angle ABC = \angle ACB = \angle BDC = y$,
在$\triangle ABD$中,根据三角形外角性质,$\angle BDC$是$\triangle ABD$的一个外角,
所以$\angle BDC=\angle A + \angle ABD$,即$y = x + x = 2x$。
因为$\angle ABC = \angle ACB = y$,而$y = 2x$,
所以在$\triangle ABC$中,$\angle ABC = \angle ACB = 2x$。
在$\triangle ABC$中,根据三角形内角和定理,$\angle A + \angle ABC + \angle ACB = 180^{\circ}$,
即$x + 2x + 2x = 180^{\circ}$。
合并同类项可得$5x = 180^{\circ}$,
解得$x = 36^{\circ}$,即$\angle A = 36^{\circ}$。
【答案】:$\angle A = 36^{\circ}$。
1.如图,∠A= 40°,∠CBD是△ABC的外角,∠CBD= 120°,则∠C的度数为(
A.90°
B.80°
C.60°
D.40°
B
)A.90°
B.80°
C.60°
D.40°
答案:
【解析】:本题可根据三角形外角的性质来求解$\angle C$的度数。
三角形外角的性质为:三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABC$中,$\angle CBD$是$\triangle ABC$的外角,已知$\angle A = 40^{\circ}$,$\angle CBD = 120^{\circ}$,根据上述性质可得$\angle CBD=\angle A + \angle C$,那么$\angle C=\angle CBD - \angle A$。
【答案】:
解:
∵$\angle CBD$是$\triangle ABC$的外角,
∴$\angle CBD=\angle A + \angle C$,
∵$\angle A = 40^{\circ}$,$\angle CBD = 120^{\circ}$,
∴$\angle C=\angle CBD - \angle A=120^{\circ}- 40^{\circ}=80^{\circ}$。
故选B。
三角形外角的性质为:三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABC$中,$\angle CBD$是$\triangle ABC$的外角,已知$\angle A = 40^{\circ}$,$\angle CBD = 120^{\circ}$,根据上述性质可得$\angle CBD=\angle A + \angle C$,那么$\angle C=\angle CBD - \angle A$。
【答案】:
解:
∵$\angle CBD$是$\triangle ABC$的外角,
∴$\angle CBD=\angle A + \angle C$,
∵$\angle A = 40^{\circ}$,$\angle CBD = 120^{\circ}$,
∴$\angle C=\angle CBD - \angle A=120^{\circ}- 40^{\circ}=80^{\circ}$。
故选B。
2.如图,已知直线$l_1,l_2,l_3$两两相交,且$l_1⊥l_3.$若α= 50°,则β的度数为(
A.120°
B.130°
C.140°
D.150°
C
)A.120°
B.130°
C.140°
D.150°
答案:
【解析】:本题主要考查了三角形外角的性质以及垂直的定义。
因为$l_1\perp l_3$,所以$l_1$与$l_3$相交形成的角中有一个角是$90^{\circ}$。
已知$\alpha = 50^{\circ}$,设$l_1$与$l_3$相交形成的另一个非直角为$\gamma$,由于$l_1$与$l_3$相交形成的两个角和为$180^{\circ}$,其中一个角是$90^{\circ}$,所以$\gamma=180^{\circ}-90^{\circ}-\alpha = 40^{\circ}$。
观察图形可知,$\beta$是直线$l_2$、$l_3$相交形成的一个外角,根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和。
在这里$\beta$相当于以$l_2$、$l_3$相交形成的三角形的一个外角,与$\beta$不相邻的两个内角分别是$90^{\circ}$和$\gamma$($\gamma = 40^{\circ}$),所以$\beta=180^{\circ}-\gamma=180^{\circ}- 40^{\circ}=140^{\circ}$。
【答案】:C。
因为$l_1\perp l_3$,所以$l_1$与$l_3$相交形成的角中有一个角是$90^{\circ}$。
已知$\alpha = 50^{\circ}$,设$l_1$与$l_3$相交形成的另一个非直角为$\gamma$,由于$l_1$与$l_3$相交形成的两个角和为$180^{\circ}$,其中一个角是$90^{\circ}$,所以$\gamma=180^{\circ}-90^{\circ}-\alpha = 40^{\circ}$。
观察图形可知,$\beta$是直线$l_2$、$l_3$相交形成的一个外角,根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和。
在这里$\beta$相当于以$l_2$、$l_3$相交形成的三角形的一个外角,与$\beta$不相邻的两个内角分别是$90^{\circ}$和$\gamma$($\gamma = 40^{\circ}$),所以$\beta=180^{\circ}-\gamma=180^{\circ}- 40^{\circ}=140^{\circ}$。
【答案】:C。
例2 如图.
(1)求证:∠BDC= ∠A+∠B+∠C;
(2)如果点D与点A分别在线段BC的两侧,猜想∠D,∠A,∠ABD,∠ACD这四个角之间有怎样的关系,并证明你的结论.
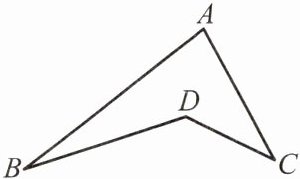
注意:本题第(1)问求证内容可作为结论记忆.
(1)求证:∠BDC= ∠A+∠B+∠C;
(2)如果点D与点A分别在线段BC的两侧,猜想∠D,∠A,∠ABD,∠ACD这四个角之间有怎样的关系,并证明你的结论.

注意:本题第(1)问求证内容可作为结论记忆.
答案:
(1)证明:连接AD并延长至点E。
∵∠BDE是△ABD的外角,
∴∠BDE=∠BAD+∠B。
∵∠CDE是△ACD的外角,
∴∠CDE=∠CAD+∠C。
∵∠BDC=∠BDE+∠CDE,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠BAD+∠B+∠CAD+∠C=∠BAC+∠B+∠C,即∠BDC=∠A+∠B+∠C。
(2)猜想:∠D+∠A+∠ABD+∠ACD=360°。
证明:连接BC。
在△ABC中,∠A+∠ABC+∠ACB=180°。
在△DBC中,∠D+∠DBC+∠DCB=180°。
∵∠ABC=∠ABD+∠DBC,∠ACB=∠ACD+∠DCB,
∴∠A+∠ABD+∠DBC+∠ACD+∠DCB+∠D=360°,即∠D+∠A+∠ABD+∠ACD=360°。
(1)证明:连接AD并延长至点E。
∵∠BDE是△ABD的外角,
∴∠BDE=∠BAD+∠B。
∵∠CDE是△ACD的外角,
∴∠CDE=∠CAD+∠C。
∵∠BDC=∠BDE+∠CDE,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠BAD+∠B+∠CAD+∠C=∠BAC+∠B+∠C,即∠BDC=∠A+∠B+∠C。
(2)猜想:∠D+∠A+∠ABD+∠ACD=360°。
证明:连接BC。
在△ABC中,∠A+∠ABC+∠ACB=180°。
在△DBC中,∠D+∠DBC+∠DCB=180°。
∵∠ABC=∠ABD+∠DBC,∠ACB=∠ACD+∠DCB,
∴∠A+∠ABD+∠DBC+∠ACD+∠DCB+∠D=360°,即∠D+∠A+∠ABD+∠ACD=360°。
查看更多完整答案,请扫码查看


