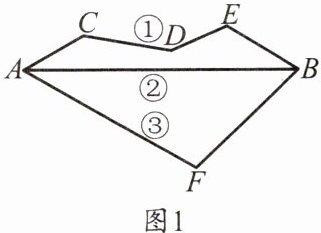
1.(1)如图1,从A地到B地有三条路可供选择,你会选择走第

(2)如图2,从P处到公路m有三条线路可走,为了尽快赶到公路上,应选择的线路是
②
条路,理由是两点之间,线段最短
.

(2)如图2,从P处到公路m有三条线路可走,为了尽快赶到公路上,应选择的线路是
PB
,理由是垂线段最短
.
答案:
1.
(1)②;两点之间,线段最短。
(2)PB;垂线段最短。
(1)②;两点之间,线段最短。
(2)PB;垂线段最短。
2.如图,在一条河MN的两岸有A,B两个小镇,现要在这条河的一岸修一个自来水泵站P,要使水泵站P到A,B铺设的主水管道的总长最小,问水泵站P应修在河岸的什么位置?请作出图形.
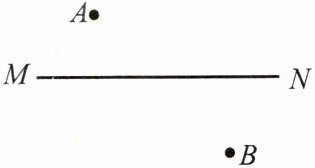
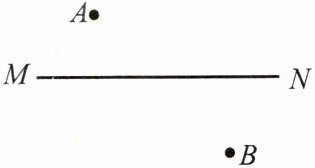
答案:
【解析】:本题主要考查最短路径问题,利用轴对称的性质找到点$A$关于直线$MN$的对称点$A'$,连接$A'B$与$MN$的交点即为水泵站$P$的位置,此时$PA + PB$的值最小。
【答案】:解:
作图步骤如下:
作点$A$关于直线$MN$的对称点$A'$;
连接$A'B$,交直线$MN$于点$P$。
则点$P$就是水泵站的位置。
图略。
【答案】:解:
作图步骤如下:
作点$A$关于直线$MN$的对称点$A'$;
连接$A'B$,交直线$MN$于点$P$。
则点$P$就是水泵站的位置。
图略。
活动1 如图1,牧民从A地出发,到一条笔直的河边l饮马,然后到B地,牧民到河边的什么地方饮马,可使所走的路径最短?


分析:我们知道若A地与B地在河的两侧,则连接AB与直线l相交的点即为饮马点;但A地与B地在直线l的同侧,于是可以考虑:如图2,假设在l上找到一点C(饮马点),把问题转化为AC+BC最短,然后进一步考虑:既然在两侧容易找,可否把AC,BC等价地放在直线l的两侧呢,于是只有用轴对称来解决,作出点B关于直线l的对称点B'(当然也可以作点A关于直线l的对称点A'),连接CB',由对称知识知AC+BC= AC+CB',由图示,显然当A,C,B'三点共线时,AC+CB'最短,即AC+BC最短.于是不难得出作图方法了.
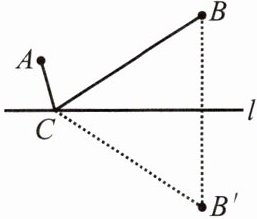


分析:我们知道若A地与B地在河的两侧,则连接AB与直线l相交的点即为饮马点;但A地与B地在直线l的同侧,于是可以考虑:如图2,假设在l上找到一点C(饮马点),把问题转化为AC+BC最短,然后进一步考虑:既然在两侧容易找,可否把AC,BC等价地放在直线l的两侧呢,于是只有用轴对称来解决,作出点B关于直线l的对称点B'(当然也可以作点A关于直线l的对称点A'),连接CB',由对称知识知AC+BC= AC+CB',由图示,显然当A,C,B'三点共线时,AC+CB'最短,即AC+BC最短.于是不难得出作图方法了.

答案:
【解析】:
本题主要考查了轴对称以及最短路径问题。
通过作点$B$关于直线$l$的对称点$B'$。
连接$AB'$,与直线$l$的交点$C$即为饮马点。
因为$B$和$B'$关于直线$l$对称,所以$CB = CB'$。
根据两点之间线段最短,当$A$,$C$,$B'$三点共线时,$AC + CB'$最短,即$AC + BC$最短。
【答案】:
作图步骤:
作点$B$关于直线$l$的对称点$B'$。
连接$AB'$,与直线$l$交于点$C$。
点$C$即为所求的饮马点。
本题主要考查了轴对称以及最短路径问题。
通过作点$B$关于直线$l$的对称点$B'$。
连接$AB'$,与直线$l$的交点$C$即为饮马点。
因为$B$和$B'$关于直线$l$对称,所以$CB = CB'$。
根据两点之间线段最短,当$A$,$C$,$B'$三点共线时,$AC + CB'$最短,即$AC + BC$最短。
【答案】:
作图步骤:
作点$B$关于直线$l$的对称点$B'$。
连接$AB'$,与直线$l$交于点$C$。
点$C$即为所求的饮马点。
1.如图,等腰△ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于点E,F.若D为BC边的中点,M为线段EF上一动点,则△CDM周长的最小值为(
A.6
B.8
C.10
D.12
C
)A.6
B.8
C.10
D.12
答案:
【解析】:本题可根据等腰三角形三线合一的性质以及线段垂直平分线的性质,通过转化线段来求解$\triangle CDM$周长的最小值。
步骤一:分析等腰三角形$\triangle ABC$的性质
已知$\triangle ABC$是等腰三角形,$D$为$BC$边的中点,根据等腰三角形三线合一的性质(等腰三角形底边上的高、底边上的中线、顶角平分线相互重合),可得$AD\perp BC$,且$AD$是$BC$的垂直平分线,同时$CD = \frac{1}{2}BC$。
因为$BC = 4$,所以$CD=\frac{1}{2}×4 = 2$。
步骤二:分析线段垂直平分线$EF$的性质
因为$EF$是$AC$的垂直平分线,根据线段垂直平分线的性质(线段垂直平分线上的点到这条线段的两个端点的距离相等),可知点$A$与点$C$关于直线$EF$对称,所以$AM = CM$。
步骤三:转化$\triangle CDM$的周长
$\triangle CDM$的周长为$CM + DM + CD$,由$AM = CM$,可得$\triangle CDM$的周长$= AM + DM + CD = AD + CD$。
步骤四:求出$AD$的长度
已知$\triangle ABC$的面积是$16$,$BC = 4$,根据三角形面积公式$S = \frac{1}{2}×底×高$,可得$\frac{1}{2}× BC× AD = 16$,即$\frac{1}{2}× 4× AD = 16$,解方程可得$AD = 8$。
步骤五:计算$\triangle CDM$周长的最小值
因为$CD = 2$,$AD = 8$,所以$\triangle CDM$周长的最小值为$AD + CD = 8 + 2 = 10$。
【答案】:C
步骤一:分析等腰三角形$\triangle ABC$的性质
已知$\triangle ABC$是等腰三角形,$D$为$BC$边的中点,根据等腰三角形三线合一的性质(等腰三角形底边上的高、底边上的中线、顶角平分线相互重合),可得$AD\perp BC$,且$AD$是$BC$的垂直平分线,同时$CD = \frac{1}{2}BC$。
因为$BC = 4$,所以$CD=\frac{1}{2}×4 = 2$。
步骤二:分析线段垂直平分线$EF$的性质
因为$EF$是$AC$的垂直平分线,根据线段垂直平分线的性质(线段垂直平分线上的点到这条线段的两个端点的距离相等),可知点$A$与点$C$关于直线$EF$对称,所以$AM = CM$。
步骤三:转化$\triangle CDM$的周长
$\triangle CDM$的周长为$CM + DM + CD$,由$AM = CM$,可得$\triangle CDM$的周长$= AM + DM + CD = AD + CD$。
步骤四:求出$AD$的长度
已知$\triangle ABC$的面积是$16$,$BC = 4$,根据三角形面积公式$S = \frac{1}{2}×底×高$,可得$\frac{1}{2}× BC× AD = 16$,即$\frac{1}{2}× 4× AD = 16$,解方程可得$AD = 8$。
步骤五:计算$\triangle CDM$周长的最小值
因为$CD = 2$,$AD = 8$,所以$\triangle CDM$周长的最小值为$AD + CD = 8 + 2 = 10$。
【答案】:C
活动2 拓展一:如图,牧民从A地出发,先到草地边某一处牧马,再到河边饮马,最后回到A处.牧民怎样走可使所走的路径最短?

拓展二:如图,牧民从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处.牧民怎样走可使所走的路径最短?
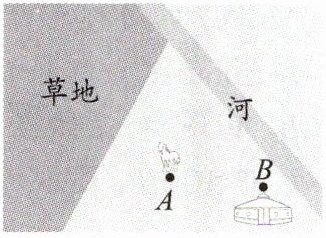
拓展三:如图,牧民每天从生活区的边沿A处出发,先到草地边的B处牧马,再到河边C处饮马,然后回到A处.如何确定A,B,C的位置,使从A处出发,到B处牧马,再到C处饮马,最后回到A处所走的路径最短?

归纳:三顶点分别在已知锐角△EGF的三边上的三角形中,以垂足三角形的周长最小.

拓展二:如图,牧民从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处.牧民怎样走可使所走的路径最短?

拓展三:如图,牧民每天从生活区的边沿A处出发,先到草地边的B处牧马,再到河边C处饮马,然后回到A处.如何确定A,B,C的位置,使从A处出发,到B处牧马,再到C处饮马,最后回到A处所走的路径最短?

归纳:三顶点分别在已知锐角△EGF的三边上的三角形中,以垂足三角形的周长最小.
答案:
【解析】:
活动2拓展一:该问题是一个典型的最短路径问题,需要利用对称点来简化问题。首先,找到A点关于草地边的对称点$A^{\prime}$,然后找到A点关于河边(设为直线l)的对称点$A^{\prime\prime}$。连接$A^{\prime}$和$A^{\prime\prime}$,该连线与草地边和河边的交点即为牧民应该选择的牧马和饮马的位置。这是因为根据对称性质,牧民从A到草地边再到河边最后回到A的路径长度等于从$A^{\prime}$到$A^{\prime\prime}$的直线距离,而直线距离是最短的。
拓展二:该问题与拓展一类似,但终点是B点。同样利用对称点的方法,找到A点关于草地边的对称点$A^{\prime}$,然后找到B点关于河边的对称点$B^{\prime}$。连接$A^{\prime}$和$B^{\prime}$,该连线与草地边和河边的交点即为牧民应该选择的牧马和饮马的位置。牧民从A出发,经过这些点后,最终到达B点,所走的路径是最短的。
拓展三:该问题稍微复杂一些,因为涉及到三个点A、B、C。但同样可以利用对称点的方法来解决。首先找到A点关于草地边(设为直线m)的对称点$A_1$,然后分别作点$A_1$关于河边(设为直线n)的对称点$A_2$和点B关于河边n的对称点$B^{\prime}$。连接$A_2$和$B^{\prime}$交河边n于点C,连接BC,再连接$A_1$C交草地边m于点B。此时,点A、B、C即为所求的位置。这是因为根据对称性质和三角形的三边关系(任意两边之和大于第三边),可以证明这样确定的A、B、C位置使得牧民所走的路径最短。
归纳部分是对前面三个拓展问题的总结和提升,指出了在锐角三角形中垂足三角形的周长最小这一规律。这实际上是对称点方法和最短路径问题的一个应用延伸。
【答案】:
活动2拓展一:作A点关于草地边和河边的对称点$A^{\prime}$、$A^{\prime\prime}$,连接$A^{\prime}$、$A^{\prime\prime}$交草地边、河边于点M、N,则路径A$\to$M$\to$N$\to$A最短。
拓展二:作A点关于草地边的对称点$A^{\prime}$、B点关于河边的对称点$B^{\prime}$,连接$A^{\prime}$、$B^{\prime}$交草地边、河边于点M、N,则路径A$\to$M$\to$N$\to$B最短。
拓展三:作A点关于草地边和河边的对称点$A_1$、$A_2$,点B关于河边的对称点$B^{\prime}$,连接$A_2$、$B^{\prime}$交河边于点C,连接$A_1$C交草地边于点B,连接CB,此时路径A$\to$B$\to$C$\to$A最短。
活动2拓展一:该问题是一个典型的最短路径问题,需要利用对称点来简化问题。首先,找到A点关于草地边的对称点$A^{\prime}$,然后找到A点关于河边(设为直线l)的对称点$A^{\prime\prime}$。连接$A^{\prime}$和$A^{\prime\prime}$,该连线与草地边和河边的交点即为牧民应该选择的牧马和饮马的位置。这是因为根据对称性质,牧民从A到草地边再到河边最后回到A的路径长度等于从$A^{\prime}$到$A^{\prime\prime}$的直线距离,而直线距离是最短的。
拓展二:该问题与拓展一类似,但终点是B点。同样利用对称点的方法,找到A点关于草地边的对称点$A^{\prime}$,然后找到B点关于河边的对称点$B^{\prime}$。连接$A^{\prime}$和$B^{\prime}$,该连线与草地边和河边的交点即为牧民应该选择的牧马和饮马的位置。牧民从A出发,经过这些点后,最终到达B点,所走的路径是最短的。
拓展三:该问题稍微复杂一些,因为涉及到三个点A、B、C。但同样可以利用对称点的方法来解决。首先找到A点关于草地边(设为直线m)的对称点$A_1$,然后分别作点$A_1$关于河边(设为直线n)的对称点$A_2$和点B关于河边n的对称点$B^{\prime}$。连接$A_2$和$B^{\prime}$交河边n于点C,连接BC,再连接$A_1$C交草地边m于点B。此时,点A、B、C即为所求的位置。这是因为根据对称性质和三角形的三边关系(任意两边之和大于第三边),可以证明这样确定的A、B、C位置使得牧民所走的路径最短。
归纳部分是对前面三个拓展问题的总结和提升,指出了在锐角三角形中垂足三角形的周长最小这一规律。这实际上是对称点方法和最短路径问题的一个应用延伸。
【答案】:
活动2拓展一:作A点关于草地边和河边的对称点$A^{\prime}$、$A^{\prime\prime}$,连接$A^{\prime}$、$A^{\prime\prime}$交草地边、河边于点M、N,则路径A$\to$M$\to$N$\to$A最短。
拓展二:作A点关于草地边的对称点$A^{\prime}$、B点关于河边的对称点$B^{\prime}$,连接$A^{\prime}$、$B^{\prime}$交草地边、河边于点M、N,则路径A$\to$M$\to$N$\to$B最短。
拓展三:作A点关于草地边和河边的对称点$A_1$、$A_2$,点B关于河边的对称点$B^{\prime}$,连接$A_2$、$B^{\prime}$交河边于点C,连接$A_1$C交草地边于点B,连接CB,此时路径A$\to$B$\to$C$\to$A最短。
查看更多完整答案,请扫码查看


