1. 三角形的定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
2. 等腰三角形的定义:有两条边相等的三角形叫作等腰三角形.
3. 等边三角形的定义:三条边都相等的三角形叫作等边三角形.
4. 三角形的分类:
(1)按角分类:
三角形$\begin{cases}直角三角形\\斜三角形\begin{cases}钝角三角形\\锐角三角形\end{cases} \end{cases}$
(2)按边分类:
三角形$\begin{cases}三边都不相等的三角形\\等腰三角形\begin{cases}底边和腰不相等的等腰三角形\\等边三角形\end{cases} \end{cases}$
5. 三角形三边之间的关系:三角形任意两边之和大于第三边,任意两边之差小于第三边.
应用:
①判断三条线段能否组成三角形的依据;
②已知三角形的两边,求第三边的取值范围.
6. 三角形三种重要的线段.
(1)三角形的中线:如图,D 为$\triangle ABC$的边 BC 的中点,则线段 AD 是$\triangle ABC$的中线.
性质:

∵AD 是$\triangle ABC$的中线,
∴$DB= DC= \frac{1}{2}BC$,
$S_{\triangle ABD}= S_{\triangle ACD}= \frac{1}{2}S_{\triangle ABC}$.
(2)三角形的角平分线:如图,$\angle DAB= \angle DAC= \frac{1}{2}\angle BAC$,则线段 AD 是$\triangle ABC$的角平分线.
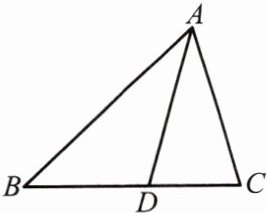
性质:
∵AD 是$\triangle ABC$的角平分线,
∴$\angle DAB= \angle DAC= \frac{1}{2}\angle BAC$.
(3)三角形的高:如图,$AD\perp BC$于点 D,
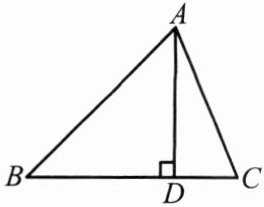
则线段 AD 是$\triangle ABC$的高.
性质:
∵AD 是$\triangle ABC$的高,
∴$\angle ADB= \angle ADC= 90^\circ$.
注意:
任何三角形都有三条中线、三条角平分线、三条高,其中三条中线、三条角平分线都分别交于一点,三条高所在直线也是交于一点的.三条中线、三条角平分线均在三角形内部,且交点也在内部;三条高不一定有交点,若有交点也不一定在三角形内部.
7. 三角形的内角和定理:三角形三个内角的和等于$180^\circ$.
应用:
(1)已知两个内角的度数,求第三个内角的度数;
(2)根据内角和为$180^\circ$列方程.
8. 三角形的外角定义:三角形一边与另一边的延长线组成的角,叫作三角形的外角.
9. 三角形内角和定理推论:三角形的外角等于与它不相邻的两个内角之和.
10. 三角形的稳定性:三角形具有稳定性,四边形具有不稳定性.
2. 等腰三角形的定义:有两条边相等的三角形叫作等腰三角形.
3. 等边三角形的定义:三条边都相等的三角形叫作等边三角形.
4. 三角形的分类:
(1)按角分类:
三角形$\begin{cases}直角三角形\\斜三角形\begin{cases}钝角三角形\\锐角三角形\end{cases} \end{cases}$
(2)按边分类:
三角形$\begin{cases}三边都不相等的三角形\\等腰三角形\begin{cases}底边和腰不相等的等腰三角形\\等边三角形\end{cases} \end{cases}$
5. 三角形三边之间的关系:三角形任意两边之和大于第三边,任意两边之差小于第三边.
应用:
①判断三条线段能否组成三角形的依据;
②已知三角形的两边,求第三边的取值范围.
6. 三角形三种重要的线段.
(1)三角形的中线:如图,D 为$\triangle ABC$的边 BC 的中点,则线段 AD 是$\triangle ABC$的中线.
性质:

∵AD 是$\triangle ABC$的中线,
∴$DB= DC= \frac{1}{2}BC$,
$S_{\triangle ABD}= S_{\triangle ACD}= \frac{1}{2}S_{\triangle ABC}$.
(2)三角形的角平分线:如图,$\angle DAB= \angle DAC= \frac{1}{2}\angle BAC$,则线段 AD 是$\triangle ABC$的角平分线.

性质:
∵AD 是$\triangle ABC$的角平分线,
∴$\angle DAB= \angle DAC= \frac{1}{2}\angle BAC$.
(3)三角形的高:如图,$AD\perp BC$于点 D,

则线段 AD 是$\triangle ABC$的高.
性质:
∵AD 是$\triangle ABC$的高,
∴$\angle ADB= \angle ADC= 90^\circ$.
注意:
任何三角形都有三条中线、三条角平分线、三条高,其中三条中线、三条角平分线都分别交于一点,三条高所在直线也是交于一点的.三条中线、三条角平分线均在三角形内部,且交点也在内部;三条高不一定有交点,若有交点也不一定在三角形内部.
7. 三角形的内角和定理:三角形三个内角的和等于$180^\circ$.
应用:
(1)已知两个内角的度数,求第三个内角的度数;
(2)根据内角和为$180^\circ$列方程.
8. 三角形的外角定义:三角形一边与另一边的延长线组成的角,叫作三角形的外角.
9. 三角形内角和定理推论:三角形的外角等于与它不相邻的两个内角之和.
10. 三角形的稳定性:三角形具有稳定性,四边形具有不稳定性.
答案:
例 1 填空题:
(1)如图,以 CD 为公共边的三角形是
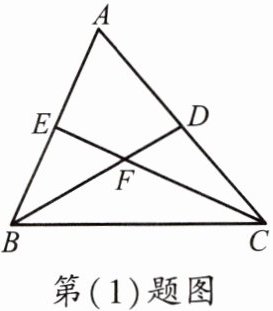

(2)五星红旗上的一颗五星的几何图案如图所示,这个图案中的等腰三角形有
(1)如图,以 CD 为公共边的三角形是
$\triangle CDE、$$\triangle CDB、$$\triangle CDA$
$,\angle EFB$是$\triangle EFB$
的内角;在$\triangle BCE$中,BE 所对的角是$\angle BCE$
$,\angle CBE$所对的边是CE
;以$\angle A$为公共角的三角形有$\triangle ABD、$$\triangle ACE、$$\triangle ABC$
.

(2)五星红旗上的一颗五星的几何图案如图所示,这个图案中的等腰三角形有
5
个.
答案:
(1)$\triangle CDE$、$\triangle CDB$、$\triangle CDA$;$\triangle EFB$;$\angle BCE$;$CE$;$\triangle ABD$、$\triangle ACE$、$\triangle ABC$
(2)5
(1)$\triangle CDE$、$\triangle CDB$、$\triangle CDA$;$\triangle EFB$;$\angle BCE$;$CE$;$\triangle ABD$、$\triangle ACE$、$\triangle ABC$
(2)5
1. 如图,图中有8个三角形,其中以 AB 为边的三角形有$\triangle ABC$、$\triangle ABD$;含$\angle ACB$的三角形有

$\triangle ABC$、$\triangle OBC$
;在$\triangle BOC$中,OC 所对的角是$\angle OBC$
,$\angle OCB$所对的边是OB
.
答案:
【解析】:
本题主要考查了三角形的边与角的对应关系,以及对给定图形中特定三角形的识别。
题目中已经给出了以$AB$为边的三角形,我们需要根据图形的特征找出含$\angle ACB$的三角形,并确定在$\triangle BOC$中$OC$所对的角和$\angle OCB$所对的边。
首先,我们识别含$\angle ACB$的三角形,通过观察图形,我们可以发现$\angle ACB$是$\triangle ABC$和$\triangle OBC$的公共角,因此含$\angle ACB$的三角形有$\triangle ABC$、$\triangle OBC$。
其次,在$\triangle BOC$中,我们需要确定$OC$所对的角和$\angle OCB$所对的边,根据三角形的边与角的对应关系,我们可以知道$OC$所对的角是$\angle OBC$,因为它们在$\triangle BOC$中处于相对的位置;同理,$\angle OCB$所对的边是$OB$。
【答案】:
含$\angle ACB$的三角形有$\triangle ABC$、$\triangle OBC$;
在$\triangle BOC$中,$OC$所对的角是$\angle OBC$,$\angle OCB$所对的边是$OB$。
本题主要考查了三角形的边与角的对应关系,以及对给定图形中特定三角形的识别。
题目中已经给出了以$AB$为边的三角形,我们需要根据图形的特征找出含$\angle ACB$的三角形,并确定在$\triangle BOC$中$OC$所对的角和$\angle OCB$所对的边。
首先,我们识别含$\angle ACB$的三角形,通过观察图形,我们可以发现$\angle ACB$是$\triangle ABC$和$\triangle OBC$的公共角,因此含$\angle ACB$的三角形有$\triangle ABC$、$\triangle OBC$。
其次,在$\triangle BOC$中,我们需要确定$OC$所对的角和$\angle OCB$所对的边,根据三角形的边与角的对应关系,我们可以知道$OC$所对的角是$\angle OBC$,因为它们在$\triangle BOC$中处于相对的位置;同理,$\angle OCB$所对的边是$OB$。
【答案】:
含$\angle ACB$的三角形有$\triangle ABC$、$\triangle OBC$;
在$\triangle BOC$中,$OC$所对的角是$\angle OBC$,$\angle OCB$所对的边是$OB$。
查看更多完整答案,请扫码查看


