例1 如图,在△ABC中,已知D是BC的中点,DF⊥AB,DE⊥AC,DF= DE.求证:AB= AC.
分析:直接证△ADB≌△ADC缺少条件,但可用“HL”证Rt△ADF≌Rt△ADE,Rt△DFB≌Rt△DEC,从而得AF= AE,FB= EC.
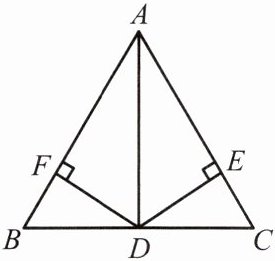
分析:直接证△ADB≌△ADC缺少条件,但可用“HL”证Rt△ADF≌Rt△ADE,Rt△DFB≌Rt△DEC,从而得AF= AE,FB= EC.

答案:
【解析】:本题可根据已知条件,利用“HL”定理证明两个直角三角形全等,进而得到对应边相等,再结合线段的和差关系证明$AB = AC$。
首先,因为$DF\perp AB$,$DE\perp AC$,所以$\triangle ADF$和$\triangle ADE$是直角三角形。
已知$D$是$BC$中点,则$BD = DC$,又已知$DF = DE$。
在$Rt\triangle ADF$和$Rt\triangle ADE$中,$AD$为公共边,根据“HL”定理(斜边和一条直角边对应相等的两个直角三角形全等),可得$Rt\triangle ADF\cong Rt\triangle ADE$,所以$AF = AE$。
同理,在$Rt\triangle DFB$和$Rt\triangle DEC$中,$BD = DC$,$DF = DE$,根据“HL”定理可得$Rt\triangle DFB\cong Rt\triangle DEC$,所以$FB = EC$。
最后,因为$AB = AF + FB$,$AC = AE + EC$,且$AF = AE$,$FB = EC$,所以$AB = AC$。
【答案】:
证明:
∵$DF\perp AB$,$DE\perp AC$,
∴$\triangle ADF$和$\triangle ADE$是直角三角形。
∵$D$是$BC$中点,
∴$BD = DC$。
又
∵$DF = DE$,
在$Rt\triangle ADF$和$Rt\triangle ADE$中,
$\begin{cases}AD = AD\\DF = DE\end{cases}$
∴$Rt\triangle ADF\cong Rt\triangle ADE(HL)$,
∴$AF = AE$。
在$Rt\triangle DFB$和$Rt\triangle DEC$中,
$\begin{cases}BD = DC\\DF = DE\end{cases}$
∴$Rt\triangle DFB\cong Rt\triangle DEC(HL)$,
∴$FB = EC$。
∵$AB = AF + FB$,$AC = AE + EC$,且$AF = AE$,$FB = EC$,
∴$AB = AC$。
首先,因为$DF\perp AB$,$DE\perp AC$,所以$\triangle ADF$和$\triangle ADE$是直角三角形。
已知$D$是$BC$中点,则$BD = DC$,又已知$DF = DE$。
在$Rt\triangle ADF$和$Rt\triangle ADE$中,$AD$为公共边,根据“HL”定理(斜边和一条直角边对应相等的两个直角三角形全等),可得$Rt\triangle ADF\cong Rt\triangle ADE$,所以$AF = AE$。
同理,在$Rt\triangle DFB$和$Rt\triangle DEC$中,$BD = DC$,$DF = DE$,根据“HL”定理可得$Rt\triangle DFB\cong Rt\triangle DEC$,所以$FB = EC$。
最后,因为$AB = AF + FB$,$AC = AE + EC$,且$AF = AE$,$FB = EC$,所以$AB = AC$。
【答案】:
证明:
∵$DF\perp AB$,$DE\perp AC$,
∴$\triangle ADF$和$\triangle ADE$是直角三角形。
∵$D$是$BC$中点,
∴$BD = DC$。
又
∵$DF = DE$,
在$Rt\triangle ADF$和$Rt\triangle ADE$中,
$\begin{cases}AD = AD\\DF = DE\end{cases}$
∴$Rt\triangle ADF\cong Rt\triangle ADE(HL)$,
∴$AF = AE$。
在$Rt\triangle DFB$和$Rt\triangle DEC$中,
$\begin{cases}BD = DC\\DF = DE\end{cases}$
∴$Rt\triangle DFB\cong Rt\triangle DEC(HL)$,
∴$FB = EC$。
∵$AB = AF + FB$,$AC = AE + EC$,且$AF = AE$,$FB = EC$,
∴$AB = AC$。
1.在下列条件中,不能判断两个直角三角形全等的是(
A.两个锐角分别对应相等
B.斜边和一个锐角分别对应相等
C.两条直角边分别对应相等
D.斜边和一条直角边分别对应相等
A
)A.两个锐角分别对应相等
B.斜边和一个锐角分别对应相等
C.两条直角边分别对应相等
D.斜边和一条直角边分别对应相等
答案:
【解析】:
本题考察的是直角三角形全等的判定条件。
A选项:两个锐角分别对应相等。在直角三角形中,如果仅知道两个锐角对应相等,并不能确定两个三角形全等,因为缺少边长的信息。
B选项:斜边和一个锐角分别对应相等。这符合直角三角形全等的$AAS$判定条件,即两个角及非夹角的一边对应相等,可以判定两个直角三角形全等。
C选项:两条直角边分别对应相等。这符合$SAS$判定条件,即两边及夹角对应相等(在直角三角形中,夹角为直角),可以判定两个直角三角形全等。
D选项:斜边和一条直角边分别对应相等。这符合直角三角形的$HL$判定条件,即斜边和一条直角边对应相等,可以判定两个直角三角形全等。
综上所述,只有A选项不能判定两个直角三角形全等。
【答案】:
A
本题考察的是直角三角形全等的判定条件。
A选项:两个锐角分别对应相等。在直角三角形中,如果仅知道两个锐角对应相等,并不能确定两个三角形全等,因为缺少边长的信息。
B选项:斜边和一个锐角分别对应相等。这符合直角三角形全等的$AAS$判定条件,即两个角及非夹角的一边对应相等,可以判定两个直角三角形全等。
C选项:两条直角边分别对应相等。这符合$SAS$判定条件,即两边及夹角对应相等(在直角三角形中,夹角为直角),可以判定两个直角三角形全等。
D选项:斜边和一条直角边分别对应相等。这符合直角三角形的$HL$判定条件,即斜边和一条直角边对应相等,可以判定两个直角三角形全等。
综上所述,只有A选项不能判定两个直角三角形全等。
【答案】:
A
2.如图,已知CE⊥AB,DF⊥AB,AF= BE,且AC= BD,则下列结论中不正确的是(
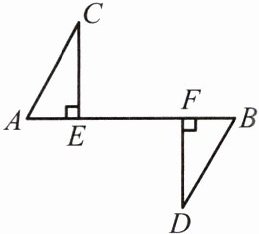
A.Rt△AEC≌Rt△BFD
B.∠C+∠B= 90°
C.∠A= ∠D
D.CE= DF
C
)
A.Rt△AEC≌Rt△BFD
B.∠C+∠B= 90°
C.∠A= ∠D
D.CE= DF
答案:
证明:
∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°(垂直定义)。
∵AF=BE,
∴AF-EF=BE-EF,即AE=BF。
在Rt△AEC和Rt△BFD中,
AC=BD,
AE=BF,
∴Rt△AEC≌Rt△BFD(HL),故A正确。
∴CE=DF(全等三角形对应边相等),故D正确。
∠A=∠B(全等三角形对应角相等)。
∵∠A+∠C=90°(直角三角形两锐角互余),
∴∠B+∠C=90°,故B正确。
∵∠A=∠B,无法直接得出∠A=∠D,故C不正确。
答案:C
∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°(垂直定义)。
∵AF=BE,
∴AF-EF=BE-EF,即AE=BF。
在Rt△AEC和Rt△BFD中,
AC=BD,
AE=BF,
∴Rt△AEC≌Rt△BFD(HL),故A正确。
∴CE=DF(全等三角形对应边相等),故D正确。
∠A=∠B(全等三角形对应角相等)。
∵∠A+∠C=90°(直角三角形两锐角互余),
∴∠B+∠C=90°,故B正确。
∵∠A=∠B,无法直接得出∠A=∠D,故C不正确。
答案:C
例2 如图,已知∠A= ∠D= 90°,AC= DB,求证:OB= OC.
分析:由∠A= ∠D= 90°,BC= CB,AC= DB,知Rt△BAC≌Rt△CDB(HL),所以AB= DC,进而易证△ABO≌△DCO,所以有OB= OC.
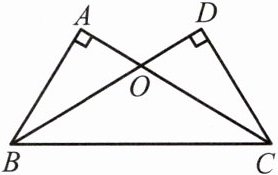
分析:由∠A= ∠D= 90°,BC= CB,AC= DB,知Rt△BAC≌Rt△CDB(HL),所以AB= DC,进而易证△ABO≌△DCO,所以有OB= OC.

答案:
【解析】:本题考查了三角形全等的判定定理和性质。首先,根据题目已知条件,我们有∠A= ∠D= 90°,这表明两个三角形都是直角三角形。又因为AC= DB且BC是两个三角形的公共边,所以我们可以利用HL(Hypotenuse-Leg)定理来证明两个三角形全等。接着,由于两个三角形全等,我们可以得出AB= DC。然后,我们可以利用这些信息来证明△ABO和△DCO全等,从而得出OB= OC。
【答案】: 证明:
∵∠A= ∠D= 90°,
∴△ABC与△DCB都是直角三角形。
在Rt△BAC和Rt△CDB中,
$ \left\{\begin{matrix}BC=CB\\AC=DB\end{matrix}\right.$
∴$Rt\triangle BAC\cong Rt\triangle CDB(HL)$。
∴$AB= DC$,
在△ABO和△DCO中,
$ \left\{\begin{matrix}\angle A=\angle D\\\angle AOB=\angle DOC\\AB=DC\end{matrix}\right.$
∴$\triangle ABO\cong\triangle DCO(AAS)$,
∴$OB= OC$。
【答案】: 证明:
∵∠A= ∠D= 90°,
∴△ABC与△DCB都是直角三角形。
在Rt△BAC和Rt△CDB中,
$ \left\{\begin{matrix}BC=CB\\AC=DB\end{matrix}\right.$
∴$Rt\triangle BAC\cong Rt\triangle CDB(HL)$。
∴$AB= DC$,
在△ABO和△DCO中,
$ \left\{\begin{matrix}\angle A=\angle D\\\angle AOB=\angle DOC\\AB=DC\end{matrix}\right.$
∴$\triangle ABO\cong\triangle DCO(AAS)$,
∴$OB= OC$。
3.如图,Rt△ABC和Rt△EDF中,∠A= ∠DEF= 90°,且点A,E,C,F共线,∠B= ∠D,在不添加任何辅助线的情况下,请你添加一个条件:
AB=ED(或BC=DF或AE=CF或AC=EF)
,使Rt△ABC和Rt△EDF全等.
答案:
AB=ED(或BC=DF或AE=CF或AC=EF)
4.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,线段AD,CE相交于点H.已知EH= EB= 3,AE= 4,则CH的长是
1
.
答案:
证明:
∵AD⊥BC,CE⊥AB,
∴∠AEH=∠CEB=∠ADB=90°。
∵∠EAH+∠B=90°,∠ECB+∠B=90°,
∴∠EAH=∠ECB。
在△AEH和△CEB中,
∠AEH=∠CEB,∠EAH=∠ECB,EH=EB,
∴△AEH≌△CEB(AAS)。
∴CE=AE=4。
∵EH=3,
∴CH=CE-EH=4-3=1。
1
∵AD⊥BC,CE⊥AB,
∴∠AEH=∠CEB=∠ADB=90°。
∵∠EAH+∠B=90°,∠ECB+∠B=90°,
∴∠EAH=∠ECB。
在△AEH和△CEB中,
∠AEH=∠CEB,∠EAH=∠ECB,EH=EB,
∴△AEH≌△CEB(AAS)。
∴CE=AE=4。
∵EH=3,
∴CH=CE-EH=4-3=1。
1
1.(1)一条射线把一个角分成两个相等的角,这条射线叫作这个角的
(2)从直线外一点到这条直线的垂线段的长度,叫作
平分线
;(2)从直线外一点到这条直线的垂线段的长度,叫作
点到直线的距离
.
答案:
【解析】:
本题主要考查了角的平分线的定义和点到直线的距离的定义。
对于(1),根据角的平分线的定义,一条射线把一个角分成两个相等的角,这条射线叫作这个角的平分线。
对于(2),根据点到直线的距离的定义,从直线外一点到这条直线的垂线段的长度,叫作点到直线的距离。
【答案】:
(1) 平分线
(2) 点到直线的距离
本题主要考查了角的平分线的定义和点到直线的距离的定义。
对于(1),根据角的平分线的定义,一条射线把一个角分成两个相等的角,这条射线叫作这个角的平分线。
对于(2),根据点到直线的距离的定义,从直线外一点到这条直线的垂线段的长度,叫作点到直线的距离。
【答案】:
(1) 平分线
(2) 点到直线的距离
2.角的平分线的性质:角的平分线上的点到角两边的
符号语言:
如图,∵ OC 平分∠AOB,点 P在 OC 上,PD⊥OA,PE⊥OB,垂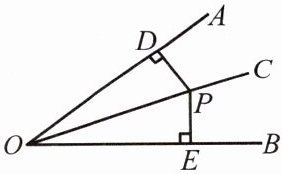
足分别为 D,E,∴ PD= PE.
(注意:不能直接得到 OD= OE)
注意:
角是一个轴对称图形,对称轴是角平分线所在直线.
距离相等
.符号语言:
如图,∵ OC 平分∠AOB,点 P在 OC 上,PD⊥OA,PE⊥OB,垂

足分别为 D,E,∴ PD= PE.
(注意:不能直接得到 OD= OE)
注意:
角是一个轴对称图形,对称轴是角平分线所在直线.
答案:
【解析】:本题考查了角平分线的性质这一知识点。该性质表明角平分线上的点到角两边的距离相等。在本题的图形情境中,已知$OC$平分$\angle AOB$,点$P$在$OC$上,且$PD\perp OA$,$PE\perp OB$,根据角平分线的性质,可直接得出$PD = PE$,这里$PD$和$PE$就是点$P$到角$\angle AOB$两边$OA$和$OB$的距离。
【答案】:距离相等
【答案】:距离相等
查看更多完整答案,请扫码查看


