3.如图,若△ABE≌△ACD,且 AB= 6,AE= 2,则 EC 的长为(

A.2
B.3
C.4
D.6
C
)
A.2
B.3
C.4
D.6
答案:
解:
∵△ABE≌△ACD,
∴AB=AC,AE=AD。
∵AB=6,
∴AC=6。
∵AE=2,
∴EC=AC - AE=6 - 2=4。
答案:C
∵△ABE≌△ACD,
∴AB=AC,AE=AD。
∵AB=6,
∴AC=6。
∵AE=2,
∴EC=AC - AE=6 - 2=4。
答案:C
4.已知△ABC 与△DEF 全等,点 A,B,C 的对应点分别为点 D,E,F,且点 E 在 AC 上,B,F,C,D 四点共线,如图所示.若∠A= 40°,∠CED= 35°,则下列结论不正确的是(
A.∠EFC= ∠ECF
B.DE= AC
C.∠B= 65°
D.∠CEF= 30°
BD
)A.∠EFC= ∠ECF
B.DE= AC
C.∠B= 65°
D.∠CEF= 30°
答案:
解:
∵△ABC≌△DEF,A,B,C对应D,E,F,
∴∠A=∠D=40°,AB=DE,BC=EF,∠B=∠EFD,∠ACB=∠FED.
∵∠CED=35°,∠D=40°,
∴∠ECD=180°-∠D-∠CED=105°,
∴∠ACB=180°-∠ECD=75°,
∴∠FED=∠ACB=75°.
∵∠CED=35°,
∴∠CEF=∠FED-∠CED=40°,故D错误.
∵BC=EF,
∴∠EFC=∠ECF,故A正确.
∵△ABC≌△DEF,
∴AC=DF,AB=DE,无法直接得出DE=AC,故B错误.
∠B=180°-∠A-∠ACB=65°,故C正确.
答案:BD
∵△ABC≌△DEF,A,B,C对应D,E,F,
∴∠A=∠D=40°,AB=DE,BC=EF,∠B=∠EFD,∠ACB=∠FED.
∵∠CED=35°,∠D=40°,
∴∠ECD=180°-∠D-∠CED=105°,
∴∠ACB=180°-∠ECD=75°,
∴∠FED=∠ACB=75°.
∵∠CED=35°,
∴∠CEF=∠FED-∠CED=40°,故D错误.
∵BC=EF,
∴∠EFC=∠ECF,故A正确.
∵△ABC≌△DEF,
∴AC=DF,AB=DE,无法直接得出DE=AC,故B错误.
∠B=180°-∠A-∠ACB=65°,故C正确.
答案:BD
5.如图,△BKC≌△BKE≌△DKC,BE 与 KD 交于点 G,KE 与 CD 交于点 P,BE 与 CD 交于点 A,∠BKC= 134°,∠E= 22°,则∠KPD=

44°
.
答案:
证明:
∵△BKE≌△DKC,
∴∠KCD=∠E=22°,∠DKC=∠BKE。
∵△BKC≌△BKE,
∴∠BKC=∠BKE=134°,
∴∠DKC=∠BKE=134°。
在△KPC中,∠KPD=∠DKC - ∠KCD=134° - 22°=44°。
结论:∠KPD=44°。
∵△BKE≌△DKC,
∴∠KCD=∠E=22°,∠DKC=∠BKE。
∵△BKC≌△BKE,
∴∠BKC=∠BKE=134°,
∴∠DKC=∠BKE=134°。
在△KPC中,∠KPD=∠DKC - ∠KCD=134° - 22°=44°。
结论:∠KPD=44°。
三角形全等的基本事实:
两边
和它们的夹角
分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
答案:
【解析】:
本题考查三角形全等的基本事实之一——SAS(边角边)判定定理。根据题目要求,需要填写两个空,分别对应SAS判定定理中的两个条件。根据三角形全等的SAS判定定理,如果两个三角形有两边及其夹角对应相等,则这两个三角形全等。题目中已经给出了“和它们的”以及“分别相等的两个三角形全等”的提示,因此第一个空应填写“两边”,第二个空应填写“夹角”。
【答案】:
两边;夹角
本题考查三角形全等的基本事实之一——SAS(边角边)判定定理。根据题目要求,需要填写两个空,分别对应SAS判定定理中的两个条件。根据三角形全等的SAS判定定理,如果两个三角形有两边及其夹角对应相等,则这两个三角形全等。题目中已经给出了“和它们的”以及“分别相等的两个三角形全等”的提示,因此第一个空应填写“两边”,第二个空应填写“夹角”。
【答案】:
两边;夹角
例1 如图,已知AC= AD,AB平分∠CAD,求证:∠C= ∠D.
分析:通过证明△ABC≌△ABD,就可以得出∠C= ∠D.由题意可知,△ABC与△ABD具备“边角边”的条件.

分析:通过证明△ABC≌△ABD,就可以得出∠C= ∠D.由题意可知,△ABC与△ABD具备“边角边”的条件.

答案:
【解析】:
本题考查了三角形全等的判定方法,具体来说是通过“边角边”(SAS)的条件来证明两个三角形全等,从而得出对应的角相等,题目中给出了$AC = AD$,$AB$平分$\angle CAD$(即$\angle CAB=\angle DAB$),再加上公共边$AB = AB$,满足全等三角形的判定定理“边角边”,进而可以证明$\triangle ABC\cong\triangle ABD$,得出$\angle C=\angle D$。
【答案】:
证明:
∵$AB$平分$\angle CAD$,
∴$\angle CAB=\angle DAB$,
在$\triangle ABC$和$\triangle ABD$中,
$\left\{\begin{matrix}AC = AD,\\\angle CAB=\angle DAB,\\AB = AB.\end{matrix}\right.$
∴$\triangle ABC\cong\triangle ABD(SAS)$,
∴$\angle C=\angle D$。
本题考查了三角形全等的判定方法,具体来说是通过“边角边”(SAS)的条件来证明两个三角形全等,从而得出对应的角相等,题目中给出了$AC = AD$,$AB$平分$\angle CAD$(即$\angle CAB=\angle DAB$),再加上公共边$AB = AB$,满足全等三角形的判定定理“边角边”,进而可以证明$\triangle ABC\cong\triangle ABD$,得出$\angle C=\angle D$。
【答案】:
证明:
∵$AB$平分$\angle CAD$,
∴$\angle CAB=\angle DAB$,
在$\triangle ABC$和$\triangle ABD$中,
$\left\{\begin{matrix}AC = AD,\\\angle CAB=\angle DAB,\\AB = AB.\end{matrix}\right.$
∴$\triangle ABC\cong\triangle ABD(SAS)$,
∴$\angle C=\angle D$。
1. 如图,AD//BC,AD= BC,要使△ADF≌△CBE,需要添加下列选项中的(
A.AE= EF
B.DF= BE
C.∠A= ∠C
D.AE= CF
D
)A.AE= EF
B.DF= BE
C.∠A= ∠C
D.AE= CF
答案:
【解析】:
首先,我们明确题目给出的条件:$AD// BC$,$AD = BC$,以及四个选项A、B、C、D分别给出的额外条件。
A. $AE = EF$:这个条件只涉及到了线段$AE$和$EF$,并没有与$\triangle ADF$和$\triangle CBE$的全等判定直接相关的信息,如角或边的对应关系。
B. $DF = BE$:虽然给出了两条边的关系,但没有给出这两条边与两个三角形的对应关系,也不能直接证明两个三角形全等。
C. $\angle A = \angle C$:这个条件给出了两个角的关系,但仅有两个角相等并不能证明两个三角形全等,还需要边的条件。
D. $AE = CF$:由于$AD// BC$,根据平行线的性质,我们有$\angle A = \angle C$(内错角相等)。
又因为$AD = BC$,且$AE = CF$,则$AF = CE$(通过线段的加减得到)。
此时,在$\triangle ADF$和$\triangle CBE$中,我们有$AD = BC$,$\angle A = \angle C$,$AF = CE$,满足$SAS$(边角边)全等条件。
因此,为了使$\triangle ADF \cong \triangle CBE$,我们需要添加的条件是$AE = CF$。
【答案】:
D
首先,我们明确题目给出的条件:$AD// BC$,$AD = BC$,以及四个选项A、B、C、D分别给出的额外条件。
A. $AE = EF$:这个条件只涉及到了线段$AE$和$EF$,并没有与$\triangle ADF$和$\triangle CBE$的全等判定直接相关的信息,如角或边的对应关系。
B. $DF = BE$:虽然给出了两条边的关系,但没有给出这两条边与两个三角形的对应关系,也不能直接证明两个三角形全等。
C. $\angle A = \angle C$:这个条件给出了两个角的关系,但仅有两个角相等并不能证明两个三角形全等,还需要边的条件。
D. $AE = CF$:由于$AD// BC$,根据平行线的性质,我们有$\angle A = \angle C$(内错角相等)。
又因为$AD = BC$,且$AE = CF$,则$AF = CE$(通过线段的加减得到)。
此时,在$\triangle ADF$和$\triangle CBE$中,我们有$AD = BC$,$\angle A = \angle C$,$AF = CE$,满足$SAS$(边角边)全等条件。
因此,为了使$\triangle ADF \cong \triangle CBE$,我们需要添加的条件是$AE = CF$。
【答案】:
D
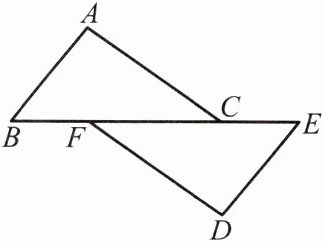
2. 如图,AB= DE,BF= EC,∠B= ∠E,求证:AC//DF.

答案:
【解析】:
本题考查了全等三角形的判定与性质以及平行线的判定。
首先,根据题目给出的条件$BF = EC$,可以得到$BF + FC = EC + FC$,即$BC = EF$。
然后,注意到题目已经给出了$AB = DE$和$\angle B = \angle E$,这构成了两个三角形$\triangle ABC$和$\triangle DEF$的两边及夹角相等的情况。
根据$SAS$(两边及夹角)全等判定定理,可以得出$\triangle ABC \cong \triangle DEF$。
由于两个三角形全等,所以它们的对应角相等,即$\angle ACB = \angle DFE$。
根据内错角相等,两直线平行,所以$AC // DF$。
【答案】:
证明:
∵$BF = EC$,
∴$BF + FC = EC + FC$,即$BC = EF$,
在$\triangle ABC$和$\triangle DEF$中,
$\left\{ \begin{matrix} AB = DE, \\\angle B = \angle E, \\BC = EF. \end{matrix} \right.$
∴$\triangle ABC \cong \triangle DEF(SAS)$,
∴$\angle ACB = \angle DFE$,
∴$AC // DF$。
本题考查了全等三角形的判定与性质以及平行线的判定。
首先,根据题目给出的条件$BF = EC$,可以得到$BF + FC = EC + FC$,即$BC = EF$。
然后,注意到题目已经给出了$AB = DE$和$\angle B = \angle E$,这构成了两个三角形$\triangle ABC$和$\triangle DEF$的两边及夹角相等的情况。
根据$SAS$(两边及夹角)全等判定定理,可以得出$\triangle ABC \cong \triangle DEF$。
由于两个三角形全等,所以它们的对应角相等,即$\angle ACB = \angle DFE$。
根据内错角相等,两直线平行,所以$AC // DF$。
【答案】:
证明:
∵$BF = EC$,
∴$BF + FC = EC + FC$,即$BC = EF$,
在$\triangle ABC$和$\triangle DEF$中,
$\left\{ \begin{matrix} AB = DE, \\\angle B = \angle E, \\BC = EF. \end{matrix} \right.$
∴$\triangle ABC \cong \triangle DEF(SAS)$,
∴$\angle ACB = \angle DFE$,
∴$AC // DF$。
例2 如图,在△ABC中,AC= BC,AC⊥BC,D为BC延长线上的点,E是AC上一点,且CE= CD.连接AD,BE,ED,则BE与AD之间有何关系?试说明你的理由.
分析:线段之间的关系要从数量关系与位置关系两个方面分析,于是不难猜想BE= AD且BE⊥AD.可结合图形猜想,然后看由已知能否得出这一结论:BE= AD且BE⊥AD.要证BE= AD,可证△BCE≌△ACD,注意∠ACB和∠ACD是一对直角;要证BE⊥AD,需要延长BE交AD于点F,然后证明∠AFE= 90°.

分析:线段之间的关系要从数量关系与位置关系两个方面分析,于是不难猜想BE= AD且BE⊥AD.可结合图形猜想,然后看由已知能否得出这一结论:BE= AD且BE⊥AD.要证BE= AD,可证△BCE≌△ACD,注意∠ACB和∠ACD是一对直角;要证BE⊥AD,需要延长BE交AD于点F,然后证明∠AFE= 90°.

答案:
【解析】:本题主要考查了全等三角形的判定与性质以及垂直的定义。
首先,根据题目已知条件$AC = BC$,$AC \perp BC$,$CE = CD$,以及$\angle ACB = \angle ACD = 90^{\circ}$,可以利用$SAS$(边角边)判定定理来证明$\triangle BCE \cong \triangle ACD$。
接着,由于$\triangle BCE \cong \triangle ACD$,根据全等三角形的性质,对应边相等,对应角相等,所以有$BE = AD$,$\angle CBE = \angle CAD$。
然后,为了证明$BE \perp AD$,可以延长$BE$交$AD$于点$F$,此时需要证明$\angle AFE = 90^{\circ}$。由于$\angle AEF$和$\angle BEC$是对顶角,所以$\angle AEF = \angle BEC$。
又因为$\angle CBE + \angle BEC = 90^{\circ}$(直角三角形的两个锐角互余),且$\angle CBE = \angle CAD$,所以$\angle CAD + \angle AEF = 90^{\circ}$。
在$\triangle AEF$中,由于$\angle CAD + \angle AEF + \angle AFE = 180^{\circ}$(三角形内角和为$180^{\circ}$),且$\angle CAD + \angle AEF = 90^{\circ}$,所以$\angle AFE = 90^{\circ}$。
因此,证明了$BE \perp AD$。
【答案】:$BE = AD$,$BE \perp AD$。
理由:
$\because AC = BC$,$AC \perp BC$,
$\therefore \angle ACB = 90^{\circ}$。
$\because CE = CD$,$\angle ACB = \angle ACD = 90^{\circ}$,
在$\triangle BCE$和$\triangle ACD$中,
$\left\{\begin{matrix}BC = AC,\\\angle ACB = \angle ACD,\\CE = CD.\end{matrix}\right.$
$\therefore \triangle BCE \cong \triangle ACD(SAS)$。
$\therefore BE = AD$,$\angle CBE = \angle CAD$。
延长$BE$交$AD$于点$F$,
$\because \angle AEF = \angle BEC$(对顶角相等),
且$\angle CBE + \angle BEC = 90^{\circ}$(直角三角形的两个锐角互余),
$\therefore \angle CAD + \angle AEF = 90^{\circ}$。
$\therefore \angle AFE = 180^{\circ} - (\angle CAD + \angle AEF) = 90^{\circ}$。
$\therefore BE \perp AD$。
首先,根据题目已知条件$AC = BC$,$AC \perp BC$,$CE = CD$,以及$\angle ACB = \angle ACD = 90^{\circ}$,可以利用$SAS$(边角边)判定定理来证明$\triangle BCE \cong \triangle ACD$。
接着,由于$\triangle BCE \cong \triangle ACD$,根据全等三角形的性质,对应边相等,对应角相等,所以有$BE = AD$,$\angle CBE = \angle CAD$。
然后,为了证明$BE \perp AD$,可以延长$BE$交$AD$于点$F$,此时需要证明$\angle AFE = 90^{\circ}$。由于$\angle AEF$和$\angle BEC$是对顶角,所以$\angle AEF = \angle BEC$。
又因为$\angle CBE + \angle BEC = 90^{\circ}$(直角三角形的两个锐角互余),且$\angle CBE = \angle CAD$,所以$\angle CAD + \angle AEF = 90^{\circ}$。
在$\triangle AEF$中,由于$\angle CAD + \angle AEF + \angle AFE = 180^{\circ}$(三角形内角和为$180^{\circ}$),且$\angle CAD + \angle AEF = 90^{\circ}$,所以$\angle AFE = 90^{\circ}$。
因此,证明了$BE \perp AD$。
【答案】:$BE = AD$,$BE \perp AD$。
理由:
$\because AC = BC$,$AC \perp BC$,
$\therefore \angle ACB = 90^{\circ}$。
$\because CE = CD$,$\angle ACB = \angle ACD = 90^{\circ}$,
在$\triangle BCE$和$\triangle ACD$中,
$\left\{\begin{matrix}BC = AC,\\\angle ACB = \angle ACD,\\CE = CD.\end{matrix}\right.$
$\therefore \triangle BCE \cong \triangle ACD(SAS)$。
$\therefore BE = AD$,$\angle CBE = \angle CAD$。
延长$BE$交$AD$于点$F$,
$\because \angle AEF = \angle BEC$(对顶角相等),
且$\angle CBE + \angle BEC = 90^{\circ}$(直角三角形的两个锐角互余),
$\therefore \angle CAD + \angle AEF = 90^{\circ}$。
$\therefore \angle AFE = 180^{\circ} - (\angle CAD + \angle AEF) = 90^{\circ}$。
$\therefore BE \perp AD$。
查看更多完整答案,请扫码查看


