1.如图,过$\triangle ABC$的顶点A作BC边上的高,以下作法正确的是 (
A
)
答案:
【解析】:本题考查了三角形的高的定义,即从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
A选项,AD是从顶点A向BC边所在直线作的垂线,符合三角形高的定义,所以该选项正确。
B选项,AD不是从顶点A向BC边作的垂线,不符合三角形高的定义,所以该选项错误。
C选项,此图中AD不是从顶点A向BC边作的垂线,不符合三角形高的定义,所以该选项错误。
D选项,此图中BD不是从顶点B向AC边作的垂线,不符合三角形高的定义,所以该选项错误。
【答案】:A
A选项,AD是从顶点A向BC边所在直线作的垂线,符合三角形高的定义,所以该选项正确。
B选项,AD不是从顶点A向BC边作的垂线,不符合三角形高的定义,所以该选项错误。
C选项,此图中AD不是从顶点A向BC边作的垂线,不符合三角形高的定义,所以该选项错误。
D选项,此图中BD不是从顶点B向AC边作的垂线,不符合三角形高的定义,所以该选项错误。
【答案】:A
2.(2022·陕西)如图,AD是$\triangle ABC$的中线,$AB= 4$,$AC= 3$.若$\triangle ACD$的周长为8,则$\triangle ABD$的周长为
9
.
答案:
【解析】:
本题可根据三角形中线的定义,得出$BD$与$BC$的关系,再结合$\triangle ACD$的周长求出$AD + DC$的值,最后根据$\triangle ABD$的周长与$AD + DC$、$AB$的关系求解。
步骤一:根据三角形中线的定义得到$BD$与$BC$的关系
三角形中线的定义为:三角形的中线是连接三角形顶点和它的对边中点的线段。
已知$AD$是$\triangle ABC$的中线,根据上述定义可知$D$为$BC$中点,即$BD = DC=\frac{1}{2}BC$。
步骤二:根据$\triangle ACD$的周长求出$AD + DC$的值
三角形的周长是三角形三边长度之和,已知$\triangle ACD$的周长为$8$,$AC = 3$,根据周长的定义可得$\triangle ACD$的周长$=AC + AD + DC = 8$,将$AC = 3$代入可得$3 + AD + DC = 8$,移项可得$AD + DC = 8 - 3 = 5$。
步骤三:求出$\triangle ABD$的周长
同样根据三角形周长的定义,$\triangle ABD$的周长$=AB + BD + AD$,由$BD = DC$,可得$\triangle ABD$的周长$=AB + DC + AD$,又因为$AB = 4$,$AD + DC = 5$,将其代入可得$\triangle ABD$的周长$= 4 + 5 = 9$。
【答案】:$9$
本题可根据三角形中线的定义,得出$BD$与$BC$的关系,再结合$\triangle ACD$的周长求出$AD + DC$的值,最后根据$\triangle ABD$的周长与$AD + DC$、$AB$的关系求解。
步骤一:根据三角形中线的定义得到$BD$与$BC$的关系
三角形中线的定义为:三角形的中线是连接三角形顶点和它的对边中点的线段。
已知$AD$是$\triangle ABC$的中线,根据上述定义可知$D$为$BC$中点,即$BD = DC=\frac{1}{2}BC$。
步骤二:根据$\triangle ACD$的周长求出$AD + DC$的值
三角形的周长是三角形三边长度之和,已知$\triangle ACD$的周长为$8$,$AC = 3$,根据周长的定义可得$\triangle ACD$的周长$=AC + AD + DC = 8$,将$AC = 3$代入可得$3 + AD + DC = 8$,移项可得$AD + DC = 8 - 3 = 5$。
步骤三:求出$\triangle ABD$的周长
同样根据三角形周长的定义,$\triangle ABD$的周长$=AB + BD + AD$,由$BD = DC$,可得$\triangle ABD$的周长$=AB + DC + AD$,又因为$AB = 4$,$AD + DC = 5$,将其代入可得$\triangle ABD$的周长$= 4 + 5 = 9$。
【答案】:$9$
3.如图,在$\triangle ABC$中,$AB= 2$,$BC= 3$,$\triangle ABC$的高AD与CE的比是_____.
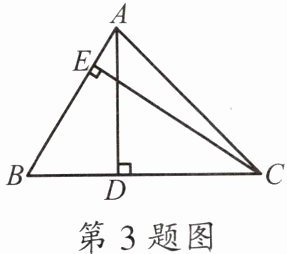

2:3
答案:
解:设△ABC的面积为S。
∵AD是BC边上的高,
∴S = $\frac{1}{2} × BC × AD = \frac{1}{2} × 3 × AD$,即$AD = \frac{2S}{3}$。
∵CE是AB边上的高,
∴S = $\frac{1}{2} × AB × CE = \frac{1}{2} × 2 × CE$,即$CE = S$。
∴$AD:CE = \frac{2S}{3}:S = 2:3$。
2:3
∵AD是BC边上的高,
∴S = $\frac{1}{2} × BC × AD = \frac{1}{2} × 3 × AD$,即$AD = \frac{2S}{3}$。
∵CE是AB边上的高,
∴S = $\frac{1}{2} × AB × CE = \frac{1}{2} × 2 × CE$,即$CE = S$。
∴$AD:CE = \frac{2S}{3}:S = 2:3$。
2:3
例2 填空题
(1)如图,在$\triangle ABC$中,已知E,F分别是AD,CE的中点,且$S_{\triangle ABC}= 24\ \text{cm}^2,$则$S_{\triangle BEF}= $
(2)如图,在$\triangle ABC$中,E是BC上的一点,EC= 2BE,D是AC的中点.设$\triangle ABC,\triangle ADF,\triangle BEF$的面积分别为$S_{\triangle ABC},S_{\triangle ADF},S_{\triangle BEF},$且$S_{\triangle ABC}= 12,$则$S_{\triangle ADF}-S_{\triangle BEF}= $
(1)如图,在$\triangle ABC$中,已知E,F分别是AD,CE的中点,且$S_{\triangle ABC}= 24\ \text{cm}^2,$则$S_{\triangle BEF}= $
6
$\text{cm}^2.$(2)如图,在$\triangle ABC$中,E是BC上的一点,EC= 2BE,D是AC的中点.设$\triangle ABC,\triangle ADF,\triangle BEF$的面积分别为$S_{\triangle ABC},S_{\triangle ADF},S_{\triangle BEF},$且$S_{\triangle ABC}= 12,$则$S_{\triangle ADF}-S_{\triangle BEF}= $
2
.(3)如图,在$\triangle ABC$中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点$G,BD= 2DC,S_{\triangle BGD}= 8,S_{\triangle AGE}= 3,$则$\triangle ABC$的面积是30
.(4)如图$,\triangle ABC$的面积是$18\ \text{cm}^2,$点D,E分别位于AB,BC上,DE// AC,且$AD= 4\ \text{cm},DB= 5\ \text{cm},$则$\triangle ABE$的面积是10
$\text{cm}^2.$
答案:
【解析】:
(1)本题主要考查三角形中线的性质,即三角形的中线将三角形分成面积相等的两部分。
因为E为AD的中点,所以$S_{\triangle BEC}=\frac{1}{2}S_{\triangle ABC}$。
已知$S_{\triangle ABC}=24cm^2$,则$S_{\triangle BEC}=12cm^2$。
又因为F为CE的中点,所以$S_{\triangle BEF}=\frac{1}{2}S_{\triangle BEC}=6cm^2$。
(2)本题可根据三角形面积与底的关系来求解。
已知$EC=2BE$,那么$S_{\triangle ABE}=\frac{1}{3}S_{\triangle ABC}$。
因为$S_{\triangle ABC}=12$,所以$S_{\triangle ABE}=4$。
由于D是AC的中点,所以$S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}=6$。
则$S_{\triangle ADF}-S_{\triangle BEF}=S_{\triangle ABD}-S_{\triangle ABE}=6 - 4 = 2$。
(3)本题可先根据E是AC的中点以及$BD = 2DC$求出相关三角形的面积,进而求出$\triangle ABC$的面积。
因为E是AC的中点,所以$S_{\triangle AGE}=S_{\triangle CGE}=3$。
又因为$BD = 2DC$,且$S_{\triangle BGD}=8$,根据等高不等底的三角形面积之比等于底之比,可得$S_{\triangle GDC}=4$。
那么$S_{\triangle ADC}=S_{\triangle BGD}+S_{\triangle GDC}=8 + 4 = 12$,$S_{\triangle BDC}=2S_{\triangle GDC}=8$,$S_{\triangle AEC}=S_{\triangle AGE}+S_{\triangle CGE}=6$,$S_{\triangle ABC}=S_{\triangle AEC}+S_{\triangle BDC}=6 + 24 = 30$。
(4)本题可先根据$AD$与$DB$的比例关系求出$\triangle ADC$与$\triangle BDC$的面积,再利用平行线的性质求出$\triangle ABE$的面积。
已知$AD = 4cm$,$DB = 5cm$,则$S_{\triangle ADC}:S_{\triangle BDC}=AD:DB = 4:5$。
又因为$S_{\triangle ABC}=18cm^2$,所以$S_{\triangle ADC}=8cm^2$,$S_{\triangle BDC}=10cm^2$。
因为$DE// AC$,所以$S_{\triangle ADE}=S_{\triangle EDC}$,那么$S_{\triangle ABE}=S_{\triangle BDC}=10cm^2$。
【答案】:
(1)$6$
(2)$2$
(3)$30$
(4)$10$
(1)本题主要考查三角形中线的性质,即三角形的中线将三角形分成面积相等的两部分。
因为E为AD的中点,所以$S_{\triangle BEC}=\frac{1}{2}S_{\triangle ABC}$。
已知$S_{\triangle ABC}=24cm^2$,则$S_{\triangle BEC}=12cm^2$。
又因为F为CE的中点,所以$S_{\triangle BEF}=\frac{1}{2}S_{\triangle BEC}=6cm^2$。
(2)本题可根据三角形面积与底的关系来求解。
已知$EC=2BE$,那么$S_{\triangle ABE}=\frac{1}{3}S_{\triangle ABC}$。
因为$S_{\triangle ABC}=12$,所以$S_{\triangle ABE}=4$。
由于D是AC的中点,所以$S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}=6$。
则$S_{\triangle ADF}-S_{\triangle BEF}=S_{\triangle ABD}-S_{\triangle ABE}=6 - 4 = 2$。
(3)本题可先根据E是AC的中点以及$BD = 2DC$求出相关三角形的面积,进而求出$\triangle ABC$的面积。
因为E是AC的中点,所以$S_{\triangle AGE}=S_{\triangle CGE}=3$。
又因为$BD = 2DC$,且$S_{\triangle BGD}=8$,根据等高不等底的三角形面积之比等于底之比,可得$S_{\triangle GDC}=4$。
那么$S_{\triangle ADC}=S_{\triangle BGD}+S_{\triangle GDC}=8 + 4 = 12$,$S_{\triangle BDC}=2S_{\triangle GDC}=8$,$S_{\triangle AEC}=S_{\triangle AGE}+S_{\triangle CGE}=6$,$S_{\triangle ABC}=S_{\triangle AEC}+S_{\triangle BDC}=6 + 24 = 30$。
(4)本题可先根据$AD$与$DB$的比例关系求出$\triangle ADC$与$\triangle BDC$的面积,再利用平行线的性质求出$\triangle ABE$的面积。
已知$AD = 4cm$,$DB = 5cm$,则$S_{\triangle ADC}:S_{\triangle BDC}=AD:DB = 4:5$。
又因为$S_{\triangle ABC}=18cm^2$,所以$S_{\triangle ADC}=8cm^2$,$S_{\triangle BDC}=10cm^2$。
因为$DE// AC$,所以$S_{\triangle ADE}=S_{\triangle EDC}$,那么$S_{\triangle ABE}=S_{\triangle BDC}=10cm^2$。
【答案】:
(1)$6$
(2)$2$
(3)$30$
(4)$10$
查看更多完整答案,请扫码查看


